非线性黏滞阻尼器性能试验
苏何先, 潘 文, 兰 香, 杨晓东, 白 羽, 张兴仙
(1.昆明理工大学 建筑工程学院,昆明 650500;2.云南省抗震工程技术研究中心,昆明 650500;3.昆明学院,昆明650214;4.云南开放大学 城市建设学院,昆明 650223)
地震和风振严重威胁人类的生存发展,为防御强震和飓风这两种自然灾害对建筑结构造成破坏而导致人们生命和财产的巨大损失,研究人员通过不断的探索,开创性的提出在建筑结构中采用消能减震技术。与传统“硬抗”措施不同,消能减震技术着力于调整或改变结构的动力特性以实现有效控制结构的震(振)动响应,从而达到保障结构地震(风振)安全的目的[1]。在建筑结构中设置黏滞阻尼器是一种经济、有效、安全、可靠的结构防震减灾措施[2-3]。黏滞阻尼器是一种典型的速度相关型被动耗能器,缸式黏滞阻尼器是建筑结构中最常用的类型,其活塞在高黏性阻尼介质中运动产生黏滞阻尼而实现耗能[4]。建筑结构中的黏滞阻尼器为结构提供附加阻尼,对刚度几乎不产生影响,因此不会改变结构的动荷载作用,在较大的频率范围内具有比较稳定的阻尼特性,从小振幅到大振幅运动都可以发挥阻尼耗能作用[5]。由于黏滞阻尼器并不对结构起支撑作用,其后期的维修和更换便利。
《建筑抗震设计规范》GB 50011—2010、《建筑消能减震技术规程》JGJ 297—2013(以下简称《消规》)等技术标准的颁布实施及近年来国家、地方先后发布的相关法律法规和产业政策利好于建筑减隔震行业的发展,行业的快速发展推动了黏滞阻尼器的工程应用,不断增长的市场需求促进了自主产品的研制[6-10],国内黏滞阻尼器研制企业快速成长,但各企业研发能力、材料技术和加工制造工艺水平的差异必然导致产品质量良莠不齐。黏滞阻尼器漏液是最容易出现的失效故障[11-13],国际上已有许多黏滞阻尼器漏液导致返工的事故[14],建筑结构中黏滞阻尼器遭受地震破坏的事例也有了报道[15],而作者在云南省抗震工程技术研究中心参与的大量黏滞阻尼器性能测试试验中也出现过漏液、缸体破坏、活塞杆屈曲、连接头断裂以及慢速试验时轴向阻力过大等产品质量问题。因此,通过性能试验进行黏滞阻尼器产品质量控制对确保消能减震结构的地震安全意义重大。
《消规》和《建筑消能阻尼器》JG/T 209—2012(以下简称《阻尼器》)系统的构建了我国建筑消能阻尼器性能试验的方法标准及技术规定,为黏滞阻尼器产品研制、工程应用及产业健康发展提供了支撑和保障。但黏滞阻尼器性能试验依据的标准体系并未明确阻尼系数和阻尼指数的确定方法,对地震疲劳性能试验滞回曲线面积评定的技术要求也不统一,导致黏滞阻尼器性能测试与评估困难。同时,慢速试验的实施及试验结果的评定等问题引起的争议也较多。针对上述黏滞阻尼器性能试验开展中常见问题进行深入的探索研究,以期为建筑黏滞阻尼器性能测试与评估技术标准完善提供参考。
1 黏滞阻尼器性能参数C、α测试
1.1 性能参数C、α测试的理论基础
黏滞阻尼器性能测试试验主要包括力学性能试验、疲劳性能试验、频率相关性试验、慢速试验、静力过载试验和极限位移试验等。通过性能试验获取的主要性能参数指标有极限位移、最大阻尼力、极限速度、阻尼指数、阻尼系数、滞回曲线及滞回曲线面积[16-17]。其中阻尼系数C和阻尼指数α不能由试验直接测量,而需要根据黏滞阻尼器的工作机理或能量原理进行试验数据处理间接得到。
黏滞阻尼器的阻尼力公式可表示为[17-18]:
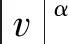
(1)
式中:Fd为黏滞阻尼器在相应位移下的阻尼力;C为黏滞阻尼器的阻尼系数;v为活塞运动的相对速度;α为黏滞阻尼器的阻尼指数,α∈(0,1]。黏滞阻尼器的α为0时具有理想的耗能滞回曲线,α为1时耗能滞回曲线接近椭圆,如图1所示。
当α较小时,在小于设计速度情况下阻尼器的耗能效率更高,减震效果更好;而在大于设计速度时,其输出力超过最大设计值的幅度也越小,即黏滞阻尼器在正常使用期间遭受到超设计地震作用时可有效避免与阻尼器连接的主体结构由于受力过大而发生损坏[19]。因此,工程常用黏滞阻尼器多为α<1的非线性黏滞阻尼器。
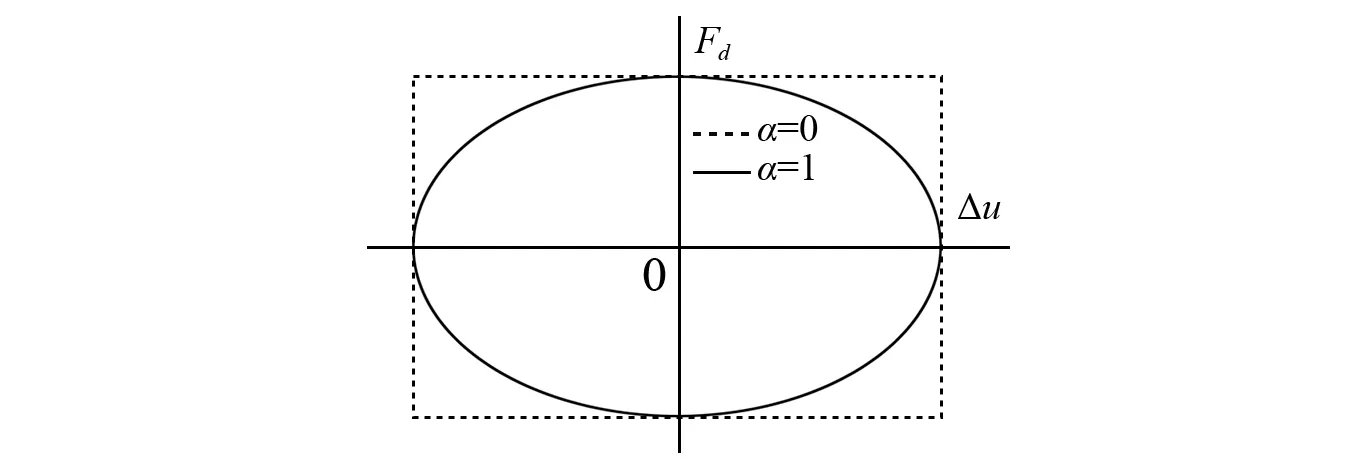
图1 黏滞阻尼器耗能滞回曲线Fig.1 Hysteresis loops of viscous damper
黏滞阻尼器的耗能能力是用结构设计中非线性黏滞阻尼器在水平地震作用下往复循环一周所消耗的能量表示的,其计算式为:
Wc=λFd maxΔu
(2)
式中:Fd max为非线性黏滞阻尼器在相应水平地震作用下的最大阻尼力,Δu为非线性黏滞阻尼器的位移,λ为阻尼指数的函数,其函数式为[18]:
(3)
式中:Γ为伽玛函数。阻尼力式(1)和耗能式(2)均可用于确定非线性黏滞阻尼器的关键性能参数C、α,但两者在数据处理中操作的便捷性及数据处理结果的一致性将直接影响非线性黏滞阻尼器的性能测试与评估。
1.2 采用阻尼力公式确定性能参数C、α
非线性黏滞阻尼器力学性能试验和疲劳性能试验均采用正弦位移控制加载,其加载位移和加载频率(加载速度)由结构设计确定。常用拟动力试验系统能够直接测得非线性黏滞阻尼器的阻尼力和位移数据,根据黏滞阻尼器的阻尼力式(1)可知,在加载速度已知的情况下,通过建立方程组可直接求解出未知参数C、α,但因加载测试系统通常未配置速度传感器,数据处理时,加载速度由测试位移求导得到,间接测量数据(计算速度)是否准确可靠将直接影响性能参数C、α的测试结果,因此,首先对计算速度结果进行校验。
(1)速度数据验证
通过外置速度传感器和位移传感器及与其配套的测试系统(试验所用SERVOTEST公司生产的拟动力加载测试系统未配置速度信号采集接入端口)进行加载位移和加载速度同步测量,对测试位移数据求导得到计算速度,并将速度传感器的实测速度与位移传感器求导所得的计算速度作对比,以验证二者是否完全一致。其中,外置位移传感器除用于保证速度信号与位移信号同步测量外,还用于校核拟动力加载测试系统的内置位移传感器并建立内外两套测试系统的数据联系。速度验证试验按黏滞阻尼器力学性能试验进行加载,图2为传感器布置示意图。
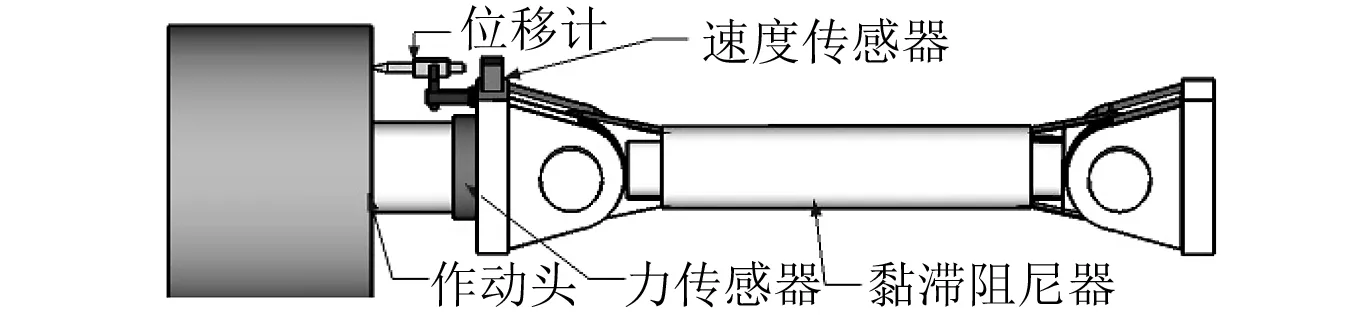
图2 传感器布置Fig.2 Sensors arrangement
利用外置位移传感器、速度传感器及拟动力阻尼器加载测试系统的配套传感器进行数据测量。由试验测试数据可知,实测速度曲线稍滞后于计算速度曲线,两者存在相位差,如图3(a)所示;计算速度由位移求导而得,两者相位差刚好为90°,如图3(b)所示;计算速度与阻尼力也不完全同步,阻尼力的相位滞后于计算速度的相位,见图3(c)。由此可见,由计算速度与实测阻尼力计算性能参数C、α必然产生误差。对比发现,实测速度与阻尼力相位的一致很好,因此,进行黏滞阻尼器性能测试时,配置同步速度传感器直接测量加载速度有利于方便准确的获得性能参数C、α。
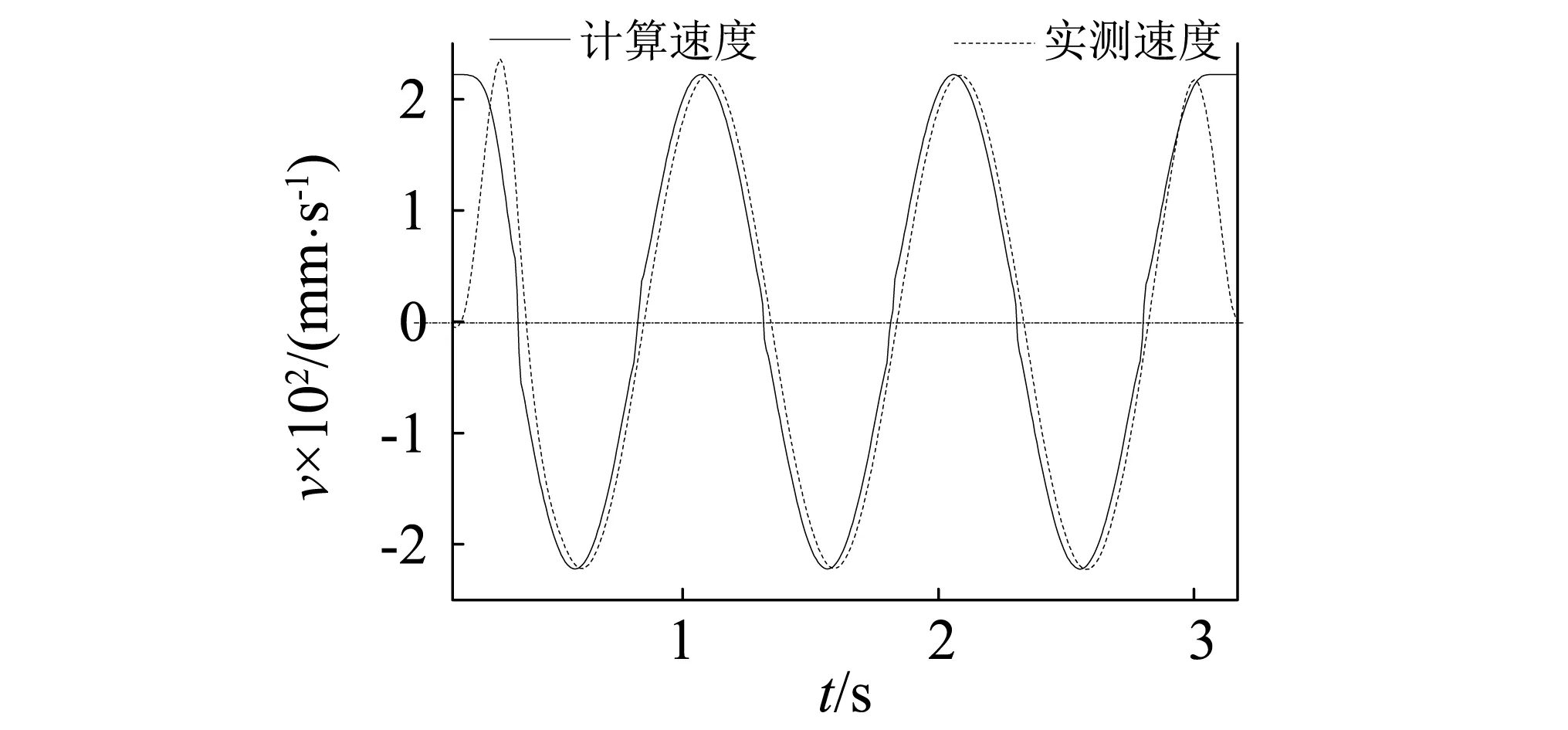
(a)计算速度与实测速度
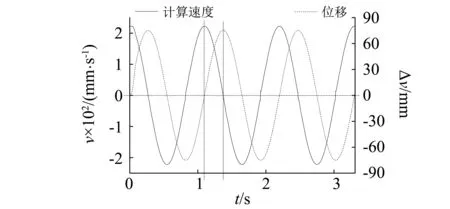
(b)加载位移与计算速度
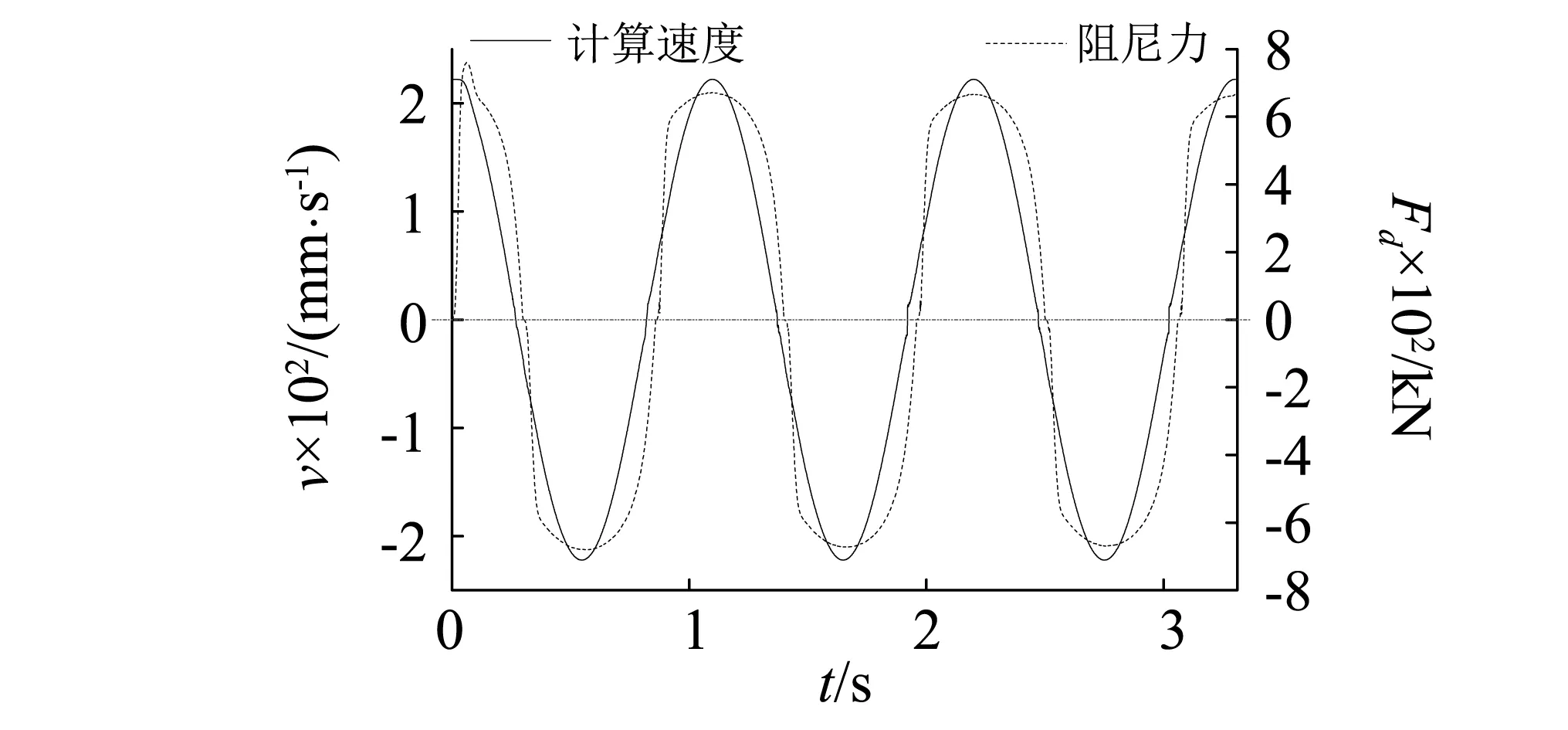
(c)计算速度与阻尼力 图3 结果曲线Fig.3 Result curves
(2)数据点选择
利用阻尼力公式(1)计算性能参数C、α时,最少需要选取两个实测数据点,针对数据点应如何选取及不同的数据选取方式是否会对测试结果产生影响展开研究。
以设计性能参数如表1的非线性黏滞阻尼器为研究对象,通过开展力学性能试验测得其设计位移工况的试验数据,并利用阻尼力公式进行数据处理。首先尝试选取两个数据点计算性能参数C、α,因涉及幂函数求解,基于方便数据处理,仅利用第一象限的数据,固定选取阻尼力和速度最大的点为第一个数据点,在剩余数据中变换选取第二个数据点,所得性能参数α结果如图4所示。

表1 非线性黏滞阻尼器设计性能参数Tab.1 Design performance parametersof nonlinear viscous damper
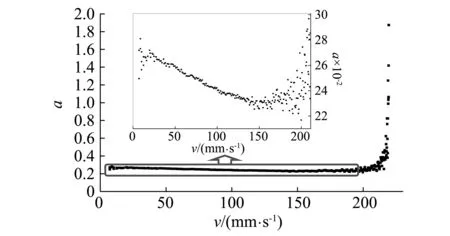
图4 数据点选择与性能参数α结果Fig.4 Relationship between data selection and results of performance parameter α
由图4可见,第二个数据点选取不同将导致阻尼指数结果差异很大,直接影响非线性黏滞阻尼器的性能评估。因此,为避免数据点选取不同对试验结果产生影响,尝试选取第3循环圈的全部数据进行幂函数拟合以获取试验性能参数。由力学性能试验数据拟合各加载位移工况下黏滞阻尼器的阻尼力-速度曲线如图5所示,幂函数拟合的试验性能参数结果见表2。
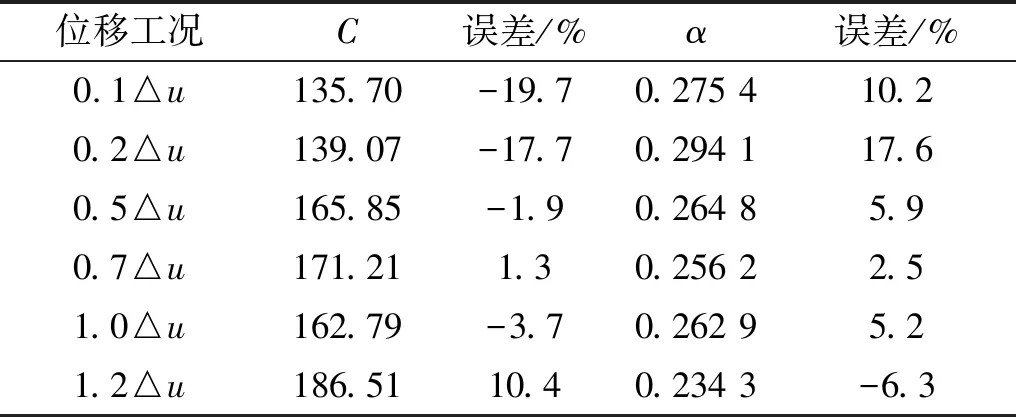
表2 性能参数C、α拟合结果Tab.2 Fitted results of performance parameters C and α
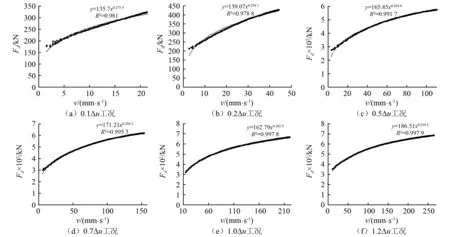
图5 曲线拟合Fig.5 Fitted curves
表2为非线性黏滞阻尼器力学性能试验六级位移工况的拟合性能参数C、α,其中0.1△u和0.2△u位移工况的C、α结果超出现行试验技术标准的误差允许范围。大量性能试验结果统计发现,多数非线性黏滞阻尼器在0.1△u和0.2△u两级位移工况下的测试C、α均存在超限,如果严格按现行标准执行,其性能试验结论均为不合格。分析认为,阻尼介质含气泡、间隙等因素均会对性能参数C、α的测试结果产生影响,而非线性黏滞阻尼器与测试设备之间不可避免的存在连接间隙,同时,为满足非线性黏滞阻尼器与测试设备连接而定制的连接销轴经常出现抗弯刚度不足,试验过程中连接销轴会产生不同程度的弯曲变形,连接间隙和销轴变形均会对非线性黏滞阻尼器的性能测试结果产生影响,小位移加载工况更为显著。因此,非线性黏滞阻尼器性能评估经常采取忽略0.1△u和0.2△u位移工况的测试C、α结果,或者以力学性能试验六级位移工况综合确定的性能参数C、α(各加载位移工况仅选取第3循环圈阻尼力和速度最大的一个数据点共六个数据点进行曲线拟合)作为性能参数C、α的测试值,而不单独确定各加载位移工况的C、α。这些处理方案在一定程度上虽避免了出现非线性黏滞阻尼器性能测试结果均无法满足现行技术标准要求的情况,却存在不能全面准确反映产品性能的可能。为实现准确测试产品性能,可考虑通过外置位移计来消除试验误差对测试结果的影响。
总之,利用阻尼力公式计算性能参数C、α需要加载速度数据,当试验设备未配备速度传感器时,计算速度由加载位移数据求导得到,由于计算速度与实际速度存在相位差,由此确定性能参数C、α必然会引入误差。利用能量原理确定非线性黏滞阻尼器的阻尼指数时,将不涉及加载速度,同时也可避免利用阻尼力公式计算性能参数C、α时数据点选取的影响。
1.3 采用耗能公式确定性能参数C、α
非线性黏滞阻尼器设计时,其性能参数是由耗能式(2)确定的,因此,性能试验可考虑采用式(2)进行数据处理以获取性能参数α,然后再利用黏滞阻尼器的阻尼力公式确定性能参数C。为便于由λ函数式(3)求解出阻尼指数α,《消规》提供了λ与α对应关系的数据表6.3.2,并提出其它数据可采用线性插值确定,即λ函数被简化为α的线性函数,在α∈(0,1]的取值范围内,其函数式可表达为λ=0.8α+3.9。因阻尼指数α是决定非线性黏滞阻尼器性能的关键因素,为准确评估非线性黏滞阻尼器的性能,对由简化λ的线性插值函数式计算阻尼指数α的误差进行分析。
(1)简化λ函数的误差
根据函数λ的表达式(3)和由《消规》提供的数据表建立的线性插值关系式λ=-0.8α+3.9,α∈(0,1],分别求解λ∈[3.1,3.9)对应的α结果,并绘制出λ与α的关系曲线,如图6所示。
由图6可知,当非线性黏滞阻尼器设计性能参数α的取值在0.364~0.823区间时,根据试验得到的λ结果,利用规范提供的简化线性插值函数式计算性能参数α,其误差小于2%,随性能参数α的设计取值向(0,1]区间的两端扩展,由简化线性函数式计算性能参
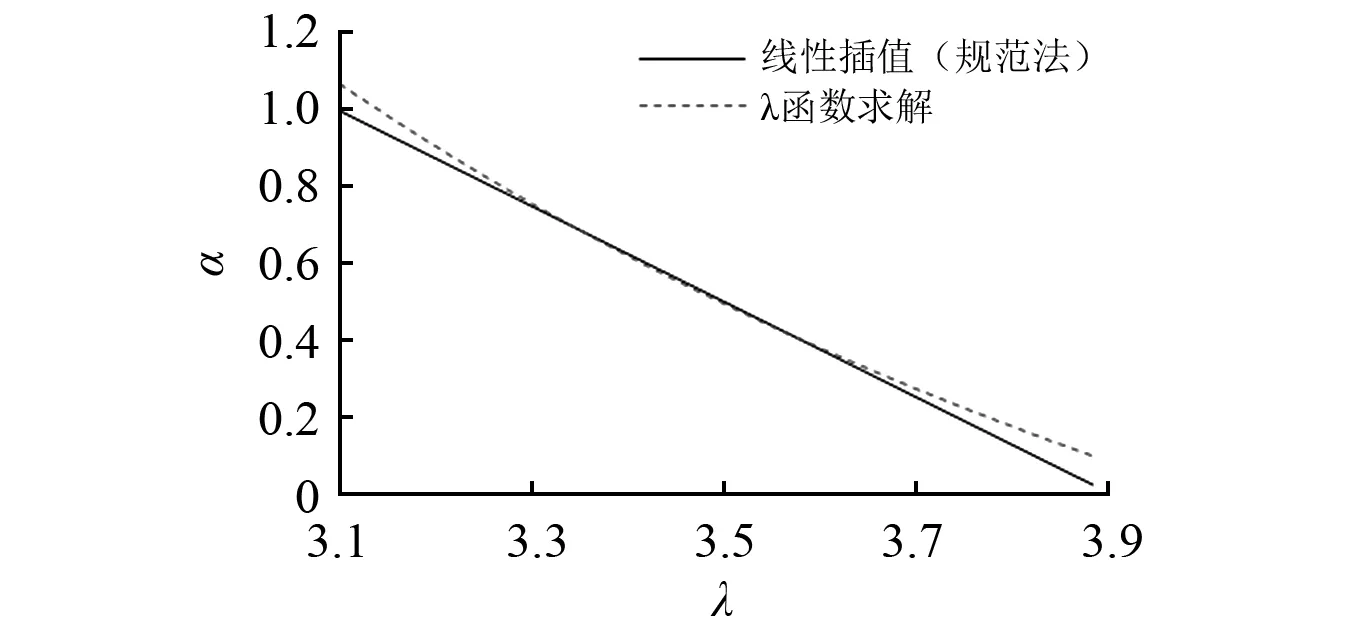
图6 λ-α关系曲线Fig.6 λ-α relation curves
数α的误差逐渐增大。当α=1时,误差为5.20%;α=0.35时,误差为2.68%;α=0.25时,误差为11.75%;α=0.15时,误差为39.50%。而房屋结构中常用的非线性黏滞阻尼器设计性能参数取值多在0.15~0.35之间,采用规范线性插值法进行试验参数计算误差较大,不利于试验人员对产品性能的准确判定,建议由函数直接求解性能参数α。
(2)利用能量原理计算性能参数C、α及误差控制
非线性黏滞阻尼器性能试验实测滞回曲线在二、四象限均存在程度不同的水平滑移段,连接间隙、充液不满和阻尼介质含气泡等都是引起滞回曲线局部畸变的主要原因。由于滞回曲线面积变小将直接影响到性能参数的确定,为定量考查滞回曲线局部畸变对采用耗能公式计算阻尼指数α的影响,对设计性能参数如表1的非线性黏滞阻尼器的试验结果展开分析。
根据力学性能试验数据,绘制各加载位移工况第3循环圈的实测阻尼力-位移滞回曲线和设计理论滞回曲线,如图7所示,实测滞回曲线面积及阻尼指数结果如表3所示。将测试阻尼器作理想化修正处理,即假定实测滞回曲线在二、四象限平顺上升,修正处理后的数据结果见表3。
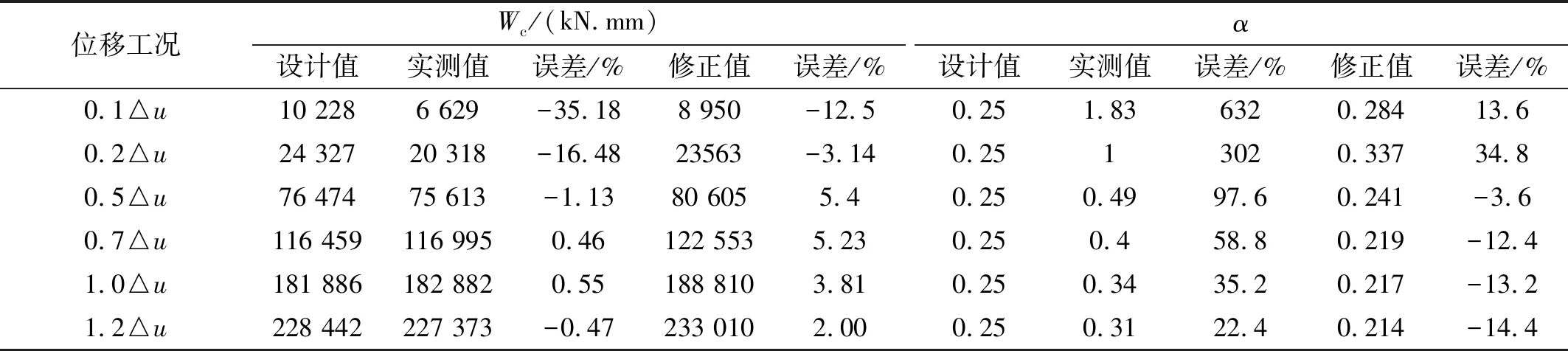
表3 滞回曲线面积及阻尼指数结果Tab.3 Results of hysteresis curves area and damping exponents
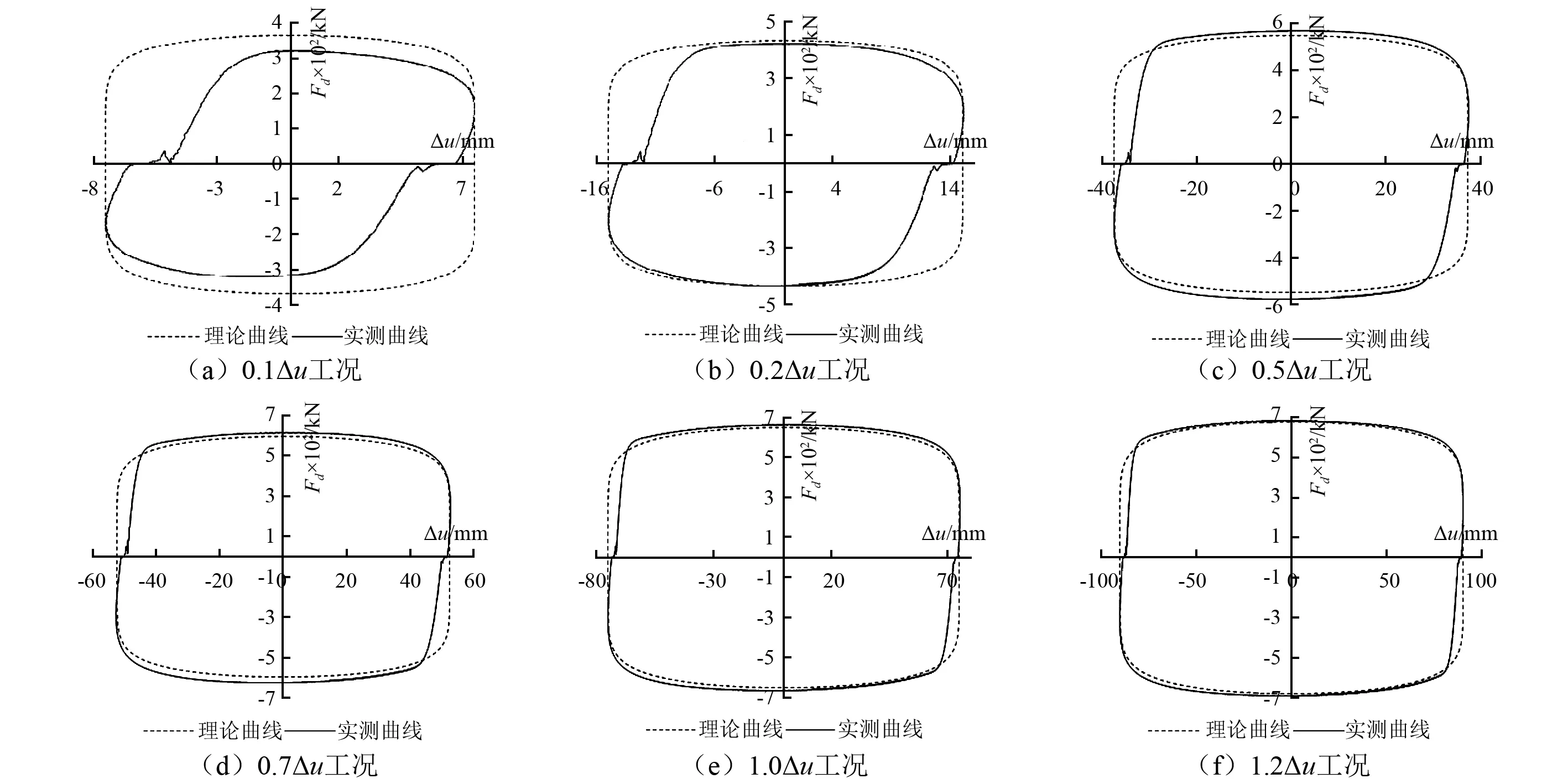
图7 设计滞回曲线与实测滞回曲线Fig.7 Comparison of design and testhysteresis loops
由表3所列数据可见,滞回曲线局部畸变对阻尼指数的影响远大于对滞回曲线面积的影响,因加载工况0.1△u和0.2△u的位移幅值相对较小,连接间隙、充液不满和阻尼介质含气泡等因素对滞回曲线面积同样会产生较大的影响,随加载位移幅值的增大,其影响逐渐减小。
测试滞回曲线经理想化修正处理后,各加载工况滞回曲线面积均增大,特别是0.1△u和0.2△u两级加载位移工况增加较多。与滞回曲线面积相比,阻尼指数的变化更显著。由此可见,由实测数据采用耗能公式求取阻尼指数α对连接间隙、充液不满和阻尼介质含气泡等影响黏滞阻尼器耗能能力的因素特别敏感,在低于设计速度时尤其明显。因此,性能测试时利用耗能公式确定的阻尼指数α能更准确的反映非线性黏滞阻尼器在低于设计速度工作状态的耗能性能。
为尽量减小试验误差,试验过程中因销轴匹配产生的连接间隙及销轴弯曲变形等导致耗能减少的问题必须得到有效控制。通过外置位移计确实能有效的解决该问题,但从非线性黏滞阻尼器性能测试的根本目的是服务于工程应用考虑,提出了将非线性黏滞阻尼器与其配套的工装件组装成套进行检测的方案,如图8(a)所示,这不仅能有效的避免图8(b)所示连接方式引入的试验误差,而且能更准确的反映非线性黏滞阻尼器安装在建筑结构中的真实性能。

(a)含工装件

(b)不含工装件 图8 黏滞阻尼器试件安装Fig.8 Installation of viscous damper specimens
1.4 确定性能参数C、α的方法分析
阻尼系数C和阻尼指数α为间接测试量,非线性黏滞阻尼器性能试验的直接测试数据经数据处理后才能得到参数C、α,参数C、α是反映非线性黏滞阻尼器性能的核心指标,数据处理方法选择是否合理将直接影响性能试验的评估结论。因此,在确保加载测试设备性能准确可靠的基础上,明确性能参数C、α的数据处理方法具有重要的现实意义。对比发现,分别利用基于黏滞阻尼器工作原理的阻尼力公式和基于能量原理的耗能公式对同一组试验数据进行处理,得到的性能参数C、α的结果差异明显,直接导致试验人员难以给定非线性黏滞阻尼器的性能评估结论。分析认为,实际产品难以完全满足理论要求、试验设备误差及试验技术手段有待改进等原因都会导致两种数据处理方式所得参数结果不一致,从非线性黏滞阻尼器在消能减震结构中所发挥的实际作用层面考虑,利用耗能公式进行数据处理更合理,其结果也能更全面的反映非线性黏滞阻尼器的实际工作性能,更利于产品质量控制和提升,但由函数λ求解阻尼指数α的难度较大,而按现行规范提供的线性插值方法确定α将会引入误差。因此,非线性黏滞阻尼器性能测试时利用耗能公式确定参数a的方法实用性较差,利用阻尼力公式进行数据处理更容易被试验人员接受。
利用阻尼力公式确定性能参数C、α需要试验的加载速度数据,而性能试验通常不进行速度的直接测试,研究表明,由加载位移求导的计算速度与实际加载速度存在相位差,这将导致间接测量参数C、α的结果不准确。因此,非线性黏滞阻尼器性能试验中配置速度传感器是其性能准确测量的重要措施。通过对采用阻尼力公式确定性能参数C、α的数据选取问题的研究表明,利用全部数据进行幂函数拟合方案更合理。非线性黏滞阻尼器性能测试时规定将黏滞阻尼器与其配套的工装连接件组装成套检测是避免试验误差的有效手段。
2 地震疲劳性能试验
地震疲劳性能试验将导致非线性黏滞阻尼器大量发热,其热性能稳定与阻尼介质的黏温性直接相关[20-21],因此,阻尼指数、阻尼系数及滞回曲线面积等均是评价其地震疲劳性能的主要性能指标,但实际测试中,考虑到阻尼指数和阻尼系数与滞回曲线面积直接相关,非线性黏滞阻尼器地震疲劳性能测试经常仅给出滞回曲线面积指标,由于阻尼指数、阻尼系数及滞回曲线面积等参数各自的特异性和温度敏感度不同,这就有可能导致评估结论不严谨。如图9(a)所示某一非线性黏滞阻尼器疲劳性能试验所得30循环圈的滞回曲线重合性较好,试验滞回曲线面积与设计滞回曲线面积的偏差范围为-14.08%~-2.89%,满足试验标准要求,但实测阻尼指数与设计阻尼指数的偏差范围为-26.13%~-5.20%,共有13个循环圈的阻尼指数不满足标准要求,阻尼系数与设计阻尼系数的最大偏差也达到17.97%。因此,非线性黏滞阻尼器地震疲劳性能试验应严格按《消规》的规定,综合考虑阻尼指数、阻尼系数及滞回曲线面积等参数在连续加载试验过程中的变化情况,全面评估非线性黏滞阻尼器的地震疲劳性能。
地震疲劳性能试验滞回曲线面积评定争议较大,《阻尼器》规定:任一循环圈滞回曲线包络面积实测值偏差应在设计值的±15%以内,实测偏差的平均值应在产品设计值的±10%以内[16];《消规》规定:实测产品在设计速度下连续加载30 圈,任一个循环的滞回曲线面积应为所有循环的滞回曲线面积平均值的±15%[17]。上述两本现行标准对滞回曲线面积的技术要求不一致,依据不同的评定标准可能出现完全不同的结论。如图9(b)为一非线性黏滞阻尼器地震疲劳试验滞回曲线,30循环圈中任一循环圈的滞回曲线面积均在所有循环圈滞回曲线面积平均值的±15%范围内,其偏差范围为-12.05%~6.62%,测试结果满足《消规》的技术指标要求,但实测滞回曲线面积与设计值的偏差范围为-17.93%~-0.80%,其中第28、第29及第30循环圈的滞回曲线面积与设计滞回曲线面积的偏差分别为-15.28%、-16.52%及-17.93%,均不满足标准要求,结合各循环圈阻尼系数及阻尼指数结果,按《阻尼器》评定非线性黏滞阻尼器地震疲劳性能试验的滞回曲线面积更合适。同时,结构消能减震设计时,非线性黏滞阻尼器预期功能的量化指标是设计值,因此,《阻尼器》的规定对非线性黏滞阻尼器性能稳定性要求更高,更利于保证消能减震结构的工作性能。
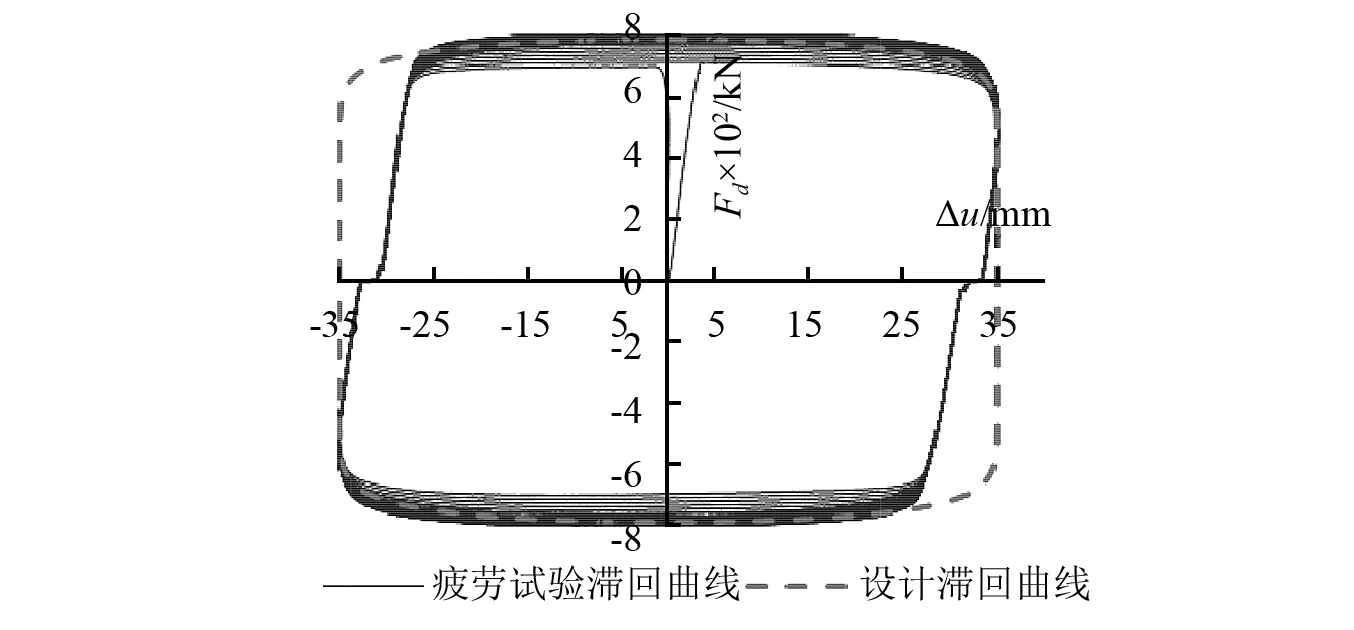
(a)设计阻尼力800 kN的黏滞阻尼器
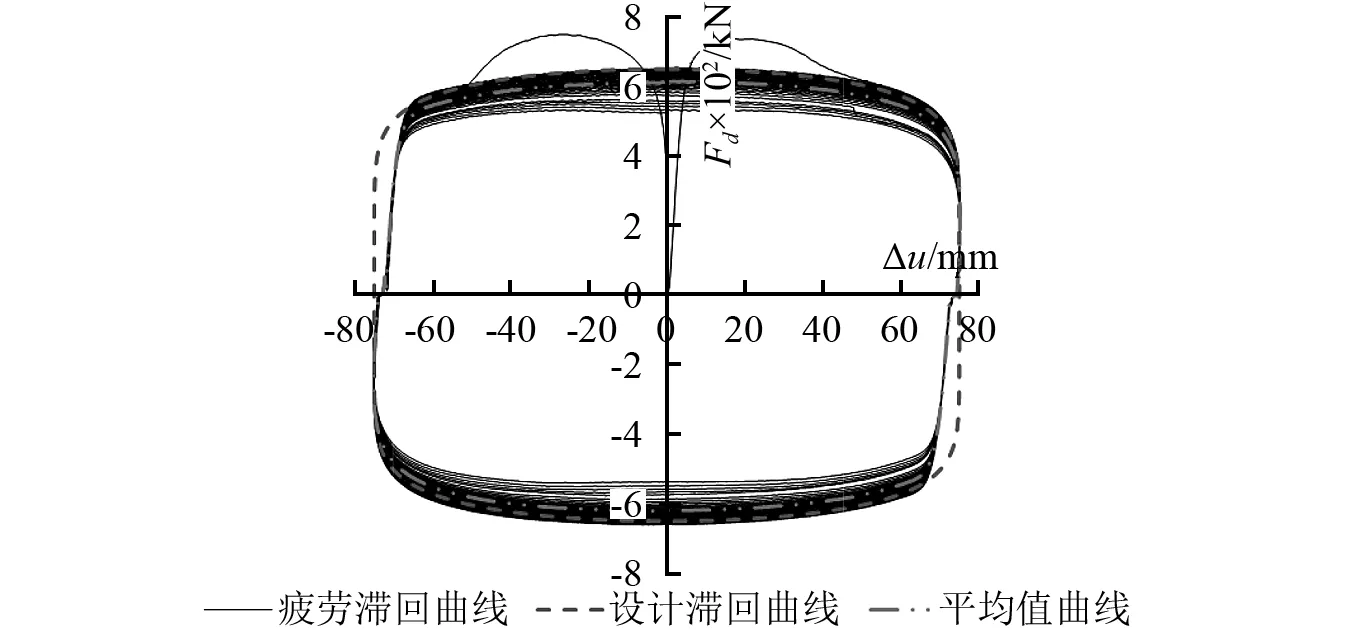
(b)设计阻尼力650 kN的黏滞阻尼器 图9 疲劳试验滞回曲线Fig.9 Hysteresisloops of fatigue test
非线性黏滞阻尼器地震疲劳性能试验所得第1循环圈和第30循环圈的滞回曲线与其余28循环圈的滞回曲线通常存在较大的差异,如图9所示,这将导致第1循环圈和第30循环圈的阻尼指数、阻尼系数甚至滞回曲线面积等不满足试验技术要求,但该差异并不完全是其耗能性能不稳定的表征,因为不论设备性能和控制程序如何优异,加载设备从静止状态到试验样品的设计速度(第1循环圈)和从试验样品的设计速度再到试验停止(第30循环圈)都存在一个伺服加速和减速的时间过程,而其加速的起点和减速的终点均设定在非线性黏滞阻尼器活塞行程的中位,这必然导致第1循环圈和第30循环圈的试验数据不能准确的反映出试样稳态的工作性能。因此,非线性黏滞阻尼器地震疲劳性能评估宜剔除第1循环圈和第30循环圈的数据,剩余任一循环圈的滞回曲线包络面积实测值偏差应控制在设计值的±15%以内,实测偏差的平均值应控制在产品设计值的±10%以内。
有机硅油是黏滞阻尼器的理解阻尼介质材料,它具有无机物二氧化硅的耐高温、不挥发、无毒无腐蚀和化学性能稳定等优异性能[20]。地震疲劳性能试验产生的高温造成阻尼介质氧化的可能性较小,但高温却可能会引起非线性黏滞阻尼器的密封件变形磨损及缸体内径改变而影响其后续工作性能,同时,现行非线性黏滞阻尼器性能试验标准未提出开展内压测试的要求,地震疲劳性能试验后拆开黏滞阻尼器进行缸体内径测量,曾出现过缸体内径改变的情况。缸体变形必然会影响到黏滞阻尼器的密封性能,国内还出现过黏滞阻尼器试验过程缸体炸裂的事故。因此,基于密封耐久和性能稳定可靠考虑,进行过地震疲劳性能测试的非线性黏滞阻尼器不建议继续使用,若欲继续在工程中使用,应对完全恢复正常状态的试样重新进行力学性能测试。
3 慢速试验
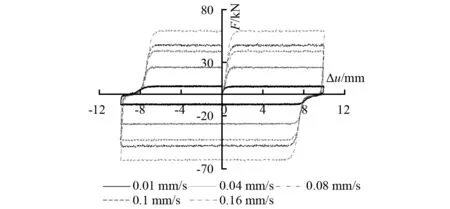
《消规》提出了非线性黏滞阻尼器应进行慢速试验的要求,但并未提供标准的试验方法和具体的技术指标要求。因此,非线性黏滞阻尼器慢速试验执行的并不严格。针对不同型号规格及同批次同型号规格的非线性黏滞阻尼器开展慢速试验,试验结果如图10所示。其中图10(a)为同批次设计阻尼力561 kN的5套非线性黏滞阻尼器的慢速试验结果,图10(b)为不同型号规格的非线性黏滞阻尼器的慢速试验结果。图示各试验曲线存在明显的差异,如何利用试验结果进行非线性黏滞阻尼器性能评估是试验人员关注的焦点。
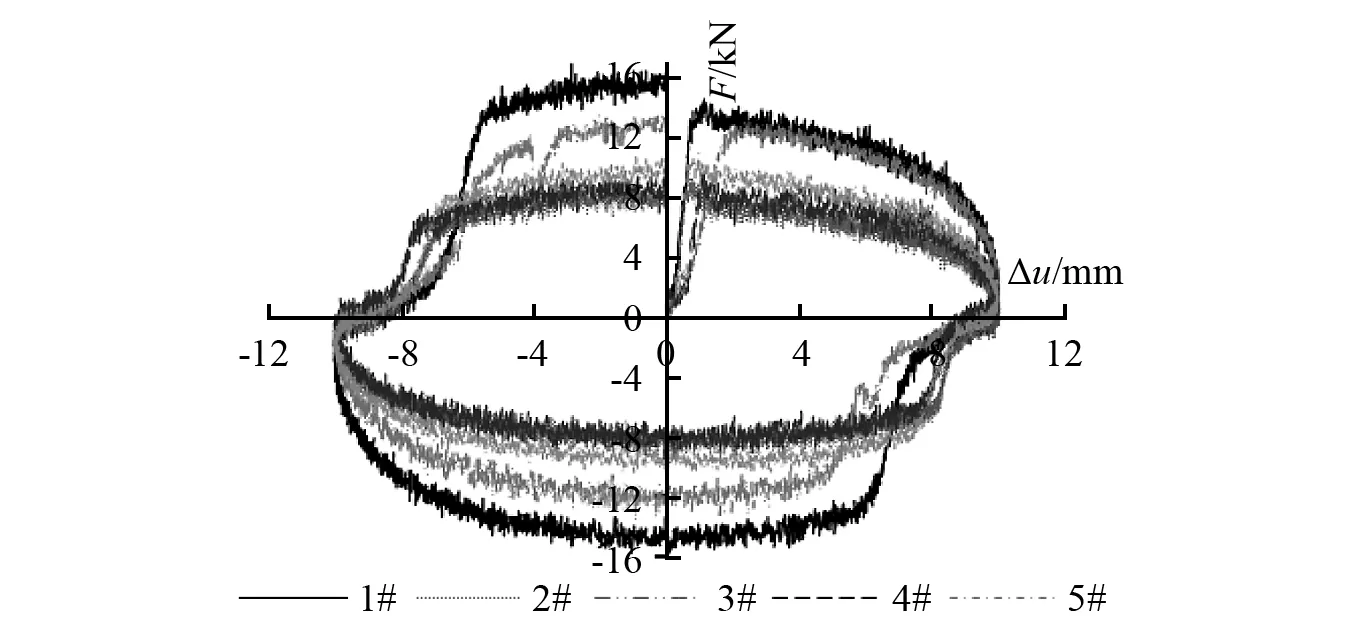
(a)同型号黏滞阻尼器
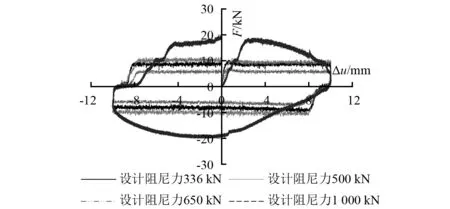
(b)不同型号黏滞阻尼器 图10 非线性黏滞阻尼器慢速试验结果Fig.10 Low velocity test results of nonlinear viscous dampers
慢速试验的目的是评估黏滞阻尼器在模拟热运动或准静态作用下的轴向阻力[22]。总结作者开展的大量非线性黏滞阻尼器慢速试验数据结果发现,慢速试验测得轴向阻力较小(轴向阻力不大于设计阻尼力的6%)的非线性黏滞阻尼器在基本力学性能试验、地震疲劳性能试验和频率相关性能试验中也都呈现出更接近设计预期的性能结果,而轴向阻力较大的非线性黏滞阻尼器的其它性能指标的测试结果也经常无法满足现行标准要求。对比欧洲标准UNI EN 15129—2009,其慢速试验轴向阻力的限制条件却是小于设计阻尼力的10%[22]。因此,在黏滞阻尼器慢速试验轴向阻力评定时就会存在顾虑,基于目前的工艺水平,如果将轴向阻力的限制条件确定为不超过设计阻尼力的6%是否过严而导致大量耗能性能良好的产品无法满足慢速试验要求;相反,如果将轴向阻力的限值确定为设计阻尼力的10%,是否又无法充分有效的发挥慢速试验对产品质量的控制作用。
UNI EN 15129—2009对慢速试验的具体规定是:匀速加载循环一周,加载速度为大于0.01 mm/s且不超过0.1 mm/s,加载位移幅值不小于10 mm,轴向阻力不超设计阻尼力的10%[22]。参照UNI EN 15129—2009,作者开展慢速试验的加载位移幅值均取为10 mm,混合采用过控制位移为正弦波和三角波的加载模式,加载频率统一为0.002 Hz。试验结果表明,加载方式不同,所得轴向阻力大小不同。因此,在确定慢速试验的轴向阻力限值之前,应先确定慢速试验的加载方法。
大量非线性黏滞阻尼器慢速试验结果表明,黏滞阻尼器的阻尼力公式在慢速试验中不再成立,但加载速度同样会影响慢速试验的轴向阻力结果,如图11所示。图11(a)为加载控制位移分别采用频率0.002 Hz的正弦波和三角波所得设计阻尼力为200 kN的非线性黏滞阻尼器的轴向阻力-位移曲线,两曲线形状明显不同,正弦波加载得到的最大轴向阻力大于三角波加载的结果,结合慢速试验的试验目的,首先可以确定慢速试验采用三角波加载更合理。由于三角波控制的加载为匀速加载,而正弦波控制的加载为变速加载,图11(a)也说明慢速试验的加载速度仍然是决定轴向阻力大小的关键因素。图11(b)为设计阻尼力为608 kN的非线性黏滞阻尼器加载速度不同时的轴向阻力-位移曲线结果。由图可见,非线性黏滞阻尼器的轴向阻力随加载速度增加而增大,加载速度为0.01 mm/s时,最大轴向阻力为设计阻尼力的1.76%;加载速度为0.1 mm/s时,最大轴向阻力为设计阻尼力的8.23%;加载速度为0.16 mm/s时,最大轴向阻力为设计阻尼力的10.36%。针对慢速试验的加载速度问题,统计了数百组加载速度采用0.08 mm/s的非线性黏滞阻尼器的慢速试验结果,仅出现过一件黏滞阻尼器的轴向阻力超过设计阻尼力的10%,而该黏滞阻尼器的设计速度为54.10 mm/s。经大量试验数据的对比分析发现,如果慢速试验的加载速度小于最大设计速度的1/2 000,具有良好性能的非线性黏滞阻尼器在慢速试验中均能实现轴向阻力不超设计阻尼力6%的限值。
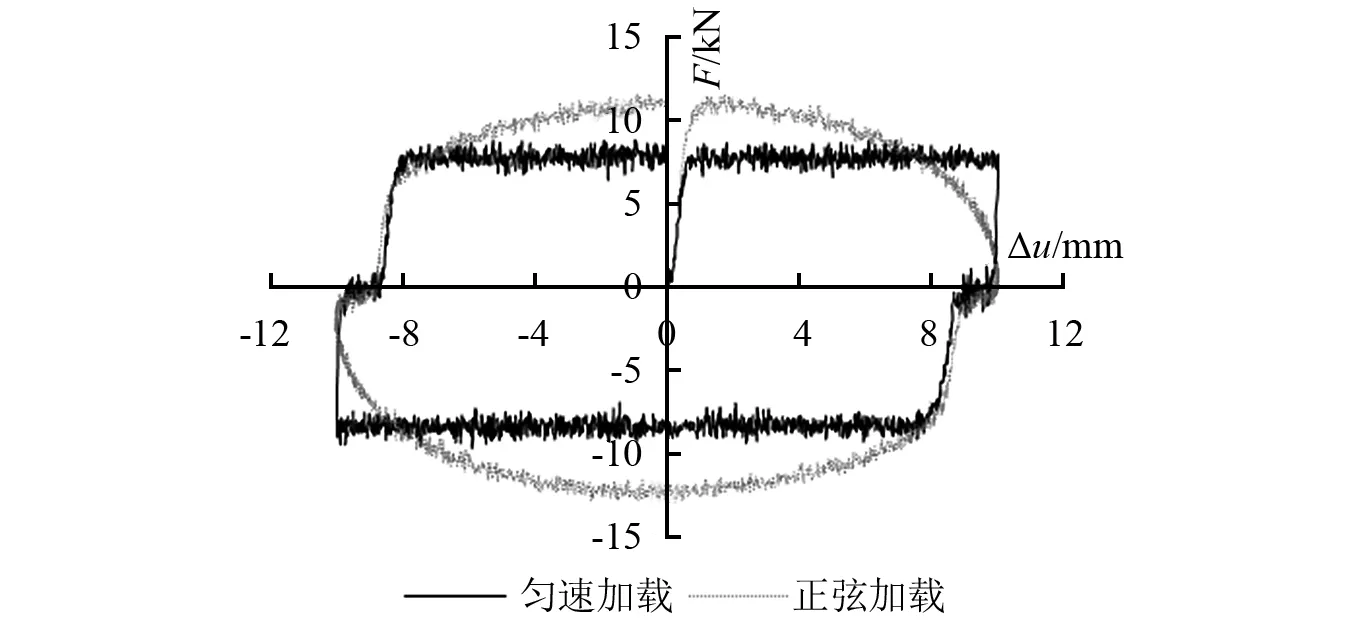
(a)加载方式不同
(b)加载速度不同 图11 加载对轴向阻力的影响Fig.11 The effect of loading on axial force resistance
4 结 论
基于工程常用非线性黏滞阻尼器的性能试验结果,结合性能测试及评估常见问题展开研究,得到以下结论:
(1)参数C、α是评估非线性黏滞阻尼器工作性能的重要指标,利用黏滞阻尼器的阻尼力公式和耗能公式进行试验数据处理均可获得C、α。耗能公式中含阻尼指数的函数λ,利用现行规范提供的线性插值法由试验λ结果求解工程常用非线性黏滞阻尼器的性能参数C、α会引入明显的误差,直接由λ函数式求解α能获得更准确的结果,但求解难度较大。因此,非线性黏滞阻尼器性能测试可优先考虑由阻尼力公式对试验阻尼力-速度数据进行幂函数拟合确定参数C、α。
(2)利用阻尼力公式确定非线性黏滞阻尼器的性能参数C、α时,配置速度传感器进行加载速度直接测量是减小试验误差的有效措施。
(3)非线性黏滞阻尼器地震疲劳性能评估应综合试验现象和各项性能参数的测试结果,避免仅考核试验现象和滞回曲线面积而忽略性能参数C、α等技术指标。数据处理时建议剔除第1和第30循环圈的试验数据,剩余各循环圈的滞回曲线包络面积实测值偏差应控制在设计值的±15%以内,实测偏差的平均值应控制在产品设计值的±10%以内。地震疲劳性能试验测试试样若在工程中继续使用,建议对恢复正常状态的试样重新进行力学性能测试。
(4)参照UNI EN 15129—2009开展了大量慢速试验并通过试验数据的分析总结,建议慢速试验加载速度宜不超过0.1 mm/s且小于非线性黏滞阻尼器最大设计速度的1/2 000,加载位移行程应不小于10 mm,轴向阻力的限值可取设计阻尼力的6%,非线性黏滞阻尼器慢速试验应采用匀速的三角波加载。
(5)非线性黏滞阻尼器性能测试时将黏滞阻尼器与其配套的工装连接件组装成套检测是减小试验误差的有效手段。

