互补集合自适应最稀疏窄带分解及其应用

陈君航， 彭延峰， 李学军， 韩清凯， 李鸿光

(1.湖南科技大学 湖南省机械设备健康维护重点实验室，湖南 湘潭 411201；2.湖南科技大学 先进矿山装备教育部工程研究中心，湖南 湘潭 411201；3.大连理工大学 机械工程学院,辽宁 大连 116024；4.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

在机械故障诊断领域中，振动信号分析与处理方法一直都是研究的热点。近年来，经验模态分解方法[1-2]和稀疏分解方法[3-5]等自适应信号分析方法得到了广泛地应用，但是稀疏分解方法需要事先根据信号的特征选择原子构成过完备原子库，缺乏自适应性，且分解得到的分量缺乏物理意义。而EMD方法存在端点效应和模态混淆等缺点。尽管Wu等[6]提出的总体平均经验模态分解方法(Ensemble Empirical Mode Decomposition，EEMD)方法对模态混淆有很好的抑制作用，但也存在如添加白噪声残留较大，分解不完备等问题。针对这些问题，Yeh等[7]提出了一种补充的总体平均经验模态分解方法CEEMD。CEEMD方法主要是通过向待分析信号中添加两个相反的白噪声信号，并分别进行EMD分解。CEEMD在保证分解效果与EEMD相当的情况下，减小了由白噪声引起的重构误差，但计算量都较大，且分解依赖添加白噪声幅值和集成次数。如果参数选择不合适，则不能抑制模态混淆且导致伪分量，无法保证分解得到分量满足IMF分量条件[8-9]。

在EMD的基础上，Peng等[10]提出了一种将信号所有数据点的优化转化为对滤波器参数的优化过程，从而可以选择合适的优化算法对滤波器参数进行优化的ASNBD方法。该方法将信号分解问题转化为非线性约束优化问题，优化目标为得到非线性信号的最优化表示，约束条件是所有内禀模态函数( Intrinsic Mode Functions，IMF)[11-12]都处于过完备字典库Dic中。ASNBD无需处理极值点，所以在抑制端点效应和模态混淆等方面优于EMD。但ASNBD仍存在一些不足，在面对噪声频率较低时，对于噪声的分解能力没有达到很好的水平。由此，基于EMD下的优化CEEMD方法，采用互补集合(Complementary Ensemble，CE)方法来优化ASNBD，得到CE-ASNBD，新的CE-ASNBD在精度上比原有的ASNBD方法得到进一步提高。

论文首先阐述了CEEMD,ASNBD和CE-ASNBD方法的基本理论，然后使用仿真信号将基于ASNBD方法、CEEMD方法和基于CE的ASNBD(CE-ASNBD)方法进行了对比，结果表明该方法能有效抑制模态混淆，表现出了更好的抗噪声性能，并具有更好的准确性和正交性。最后，论文将基于CE的ASNBD方法应用于滚动轴承的故障诊断，结果表明该方法能有效应用于滚动轴承机械故障诊断。

1 基于CE的ASNBD优化方法

1.1 ASNBD

1.1.1 内禀窄带分量

信号S(t)一般能够表示为A(t)cos(ωt+φ(t))的形式。如果A(t)是带限的，它的最大频率远小于ω，且φ(t)是“缓变”相位函数，则信号S(t)称为窄带信号。窄带信号的概念可以推广到局部窄带信号。如果对于S(t)的任一时间点，都存在一个邻域区间，使得S(t)在该区间中近似于窄带信号，则信号S(t)称为局部窄带信号。

若使用信号分解方法得到的分量满足局部窄带信号的条件，称其为内禀窄带分量[13]。

1.1.2 奇异局部线性算子

从L2(R)到L2(R)的线性算子T称为局部线性算子，若t∈R，t存在的领域Bt，使得

T(s)(t)=T(s|Bt)(t),(∀s∈L2(R) )

(1)

式中:s|Bt表示s在Bt上的限制。若T奇异，称T为奇异局部算子。论文中奇异局部算子如下

(2)

式中：极小化T(s)2意味着s处于算子T的局部窄带空间[13]。

1.1.3 ASNBD方法的步骤

ASNBD方法首先建立过完备字典库Dic为:

Dic={A(t)cos(ωt+φ(t))}

(3)

式中:A(t)的最大频率远小于ω；φ(t)是缓变函数。

在建立了过完备字典库Dic以后，为了寻找到最佳的内禀稀疏结构，将信号分解问题转换成如下无约束优化问题P2，从而得到信号的最稀疏解。信号的迭代过程如下：

1)令r1(t)=f(t)；

2)解决如下优化问题P2：

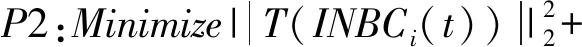
(4)

定义INBCi(t)满足式(4)所示过完备字典库Dic的条件，即INBCi(t)为局部窄带信号。D是微分算子，用于规范INBCi(t)。

3)令ri+1=ri(t)-INBCi(t)；

4)若‖ri+1‖2<ε则迭代终止，否则返回到第二步。

1.2 CE-ASNBD

1.2.1 CE

互补集合(Complementary Ensemble,CE)方法来源于CEEMD算法，该方法以正负成对的形式向原始信号中加入辅助白噪声，过程如下：

首先设置辅助白噪声的强度，通过matlab来使用标准差函数std(s)计算原信号s的标准差，使原信号除以标准差函数得到新的函数S，再通过引入随机函数randn

temp=randn(1,1)*NstdX1=S+tempX2=S-temp

(5)

再令s1=X1*sstd;s2=X2*sstd，即可得到一组添加了相反的辅助白噪声的信号，通过控制Nstd的大小可以设置辅助白噪声的强度。

然后将固定强度的白噪声加入原信号中，然后进行EMD分解,得到一个IMF分量，然后继续加N组不同白噪声分别进行相应次数的分解，对获得的分量进行总体平均，得

(6)

式中：IMF是一阶分量；N表示加入不同白噪声次数；Ei表示EMD分解产生的第i个分量；ε表示加入噪声的比例；ωi表示加入白噪声[14]。这个方法使用在EMD中解决模态混叠问题，很好地消除重构信号的残余辅助噪声，而且噪声实现次数可以较低，提高了计算效率。

1.2.2 CE-ASNBD

ASNBD方法在处理信号上有很多优势，但其也存在一些缺点，在面对一些低频率的噪声中，分解的效果比较差。由此本文受EEMD优化后的CEEMD方法启发，通过互补集合(Complementary Ensemble,CE)方法来优化ASNBD，使其精度更精确。算法的迭代过程如下：

1)在原始信号中加入N组固定强度成对白噪声ntN，符号相反，得到一系列信号：

R1(t)=r1,1(t)，r1,2(t)，r1,2(t)，r2,2(t),……r1,N(t)，r2,N(t)r1,1(t)=f(t)+nt1r1,2(t)=f(t)-nt1……r1,N(t)=f(t)+ntNr1,N(t)=f(t)-ntN

2)解决如下优化问题P2：

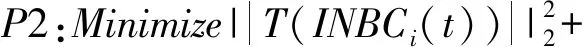
(7)

定义INBCi(t)满足式(4)所示过完备字典库Dic的条件，即INBCi(t)为局部窄带信号。D是微分算子，用于规范INBCi(t)。将上述一些列信号代入其中得到2N个INBC分量，两两为一组，分别是INBC1,INBC2……INBC2N-1,INBC2N，对获得的INBC分量进行整体平均，得

(8)

其中INBC1,1是一阶INBC分量，N表示加入不同噪声的次数。接着，计算减去第一阶INBC分量的残差，令

Ri+1=Ri(t)-INBCi(t)

(9)

4)若‖Ri+1‖2<ε则迭代终止，否则返回到第二步。若f(t)为N×1向量，则上述优化问题P2需要同时对N个参数进行优化，计算量极为巨大。为减小计算量，论文使用基于滤波器参数优化的迭代过程解决优化问题P2。

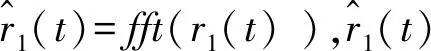
2)建立滤波器Χ(k|λ)如下

(10)

式中：λ=[ω,ωc,ωb]

3)解决如下非线性无约束优化问题P3:

(11)

4)得到最优参数λ0后，令

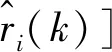
(12)

CE-ASNBD方法同CEEMD方法一样，通过利用加入的白噪声均值为零的特性，以正负成对的形式向原始信号中加入辅助白噪声，并使用多次循环计算平均使信号中的噪声相互抵消。CE-ASNBD相比于原有的ASNBD方法，即使是在面对一些低频率的噪声中，对信号的精确度上也有准确的提升。CE-ASNBD方法的流程图如图1所示。

2 仿真对比分析

为了说明CE-ASNBD方法的优越性，使用ASNBD和EMD与其进行对比分析。首先，不失一般性质的，对以下仿真信号x(t)进行考虑：

(13)

式中：混合信号y(t)由信号x1(t)，信号x2(t)和白噪声n(t)组成，混合信号中噪声为间歇噪声，有两段白噪声信号，每段信号噪声时间为0.1 s，信噪比为12 dB。混合信号y(t)及其分量的时域波形如图2所示。图2中(a)为y(t)时域波形，(b)为x1(t)时域波形，图(c)为

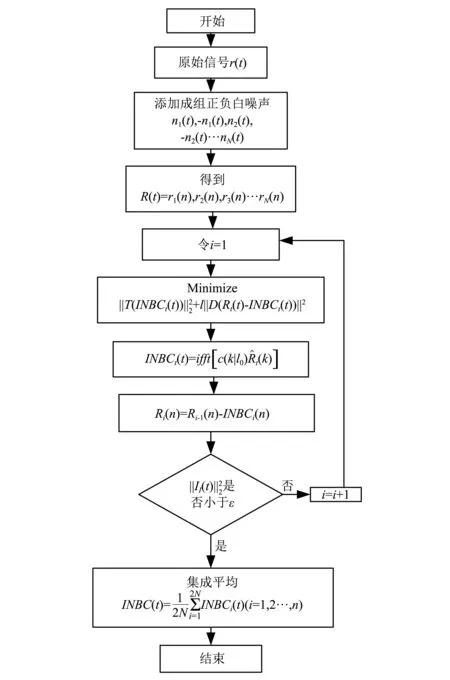
图1 CE-ASNBD方法流程图示Fig.1 Flow chart of CE-ASNBD method

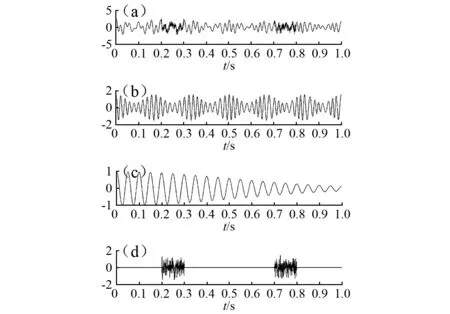
图2 混合信号y(t)及其分量的时域波形Fig.2 Time domain waveform of mixed signal y(t) and its components

x2(t)时域波形，图(d)为间歇白噪声信号n(t)时域波形。分别采用CE-ASNBD方法、CEEMD方法和ASNBD方法对y(t)进行分解。三种方法的分解结果分别如图3、图4和图5所示。

从图3、图4和图5可以看出CE-ASNBD分解出来的分量幅值较为平稳，和真实值较为接近，残余量和噪声信号的误差较小。ASNBD方法得到的INBC1由于噪声信号的干扰还是产生了模态混淆，CEEMD方法得到的分量出现了严重模态混淆，未能得到准确有效分量。

图3 原始信号y(t)的CE-ASNBD分解结果Fig.3 CE-ASNBD decomposition results of original signal y(t)

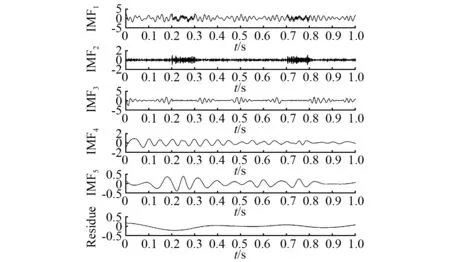
图4 原始信号y(t)的CEEMD分解结果Fig.4 CEMD decomposition results of original signal y(t)

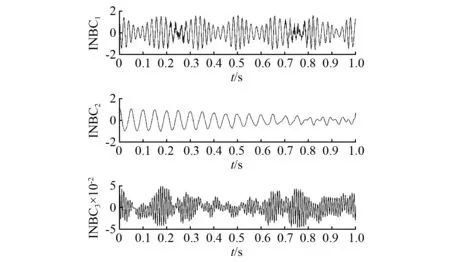
图5 原始信号y(t)的ASNBD分解结果Fig.5 ASNBD decomposition results of original signal y(t)

为更深入地比较分解结果，论文考虑相关性系数r、能量误差E及正交性指标IOjk[15]。三种方法得到的分量与实际分量的上述参数如表1所示，其中ri和Ei为分解得到的第i个实际分量与其相对应的分解得到的分量之间的比较结果，IOjk为分解得到的第i个分量和第j个分量之间的正交性指标。分析结果表明CE-ASNBD方法拥有更好的相关性和正交性，且能量误差更小。上述分析结果表明，CE-ASNBD方法对含噪声干扰引起的模态混淆有很好的抑制作用，分解得到的信号更准确，且由于拥有更好的正交性，因此能量泄露更小。CE-ASNBD方法、ASNBD方法和CEEMD方法的计算时间分别为30 s、16 s及10 s。CE-ASNBD方法的计算时长要高于其它两种方法，所以它的效率有待提高。

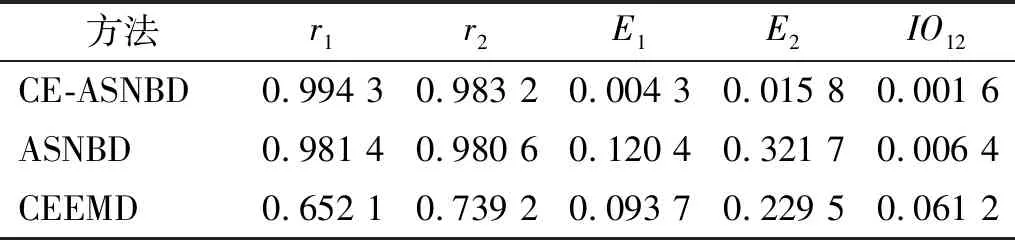
表1 CE-ASNBD、CEEMD和ASNBD的参数对比Tab.1 Parametric comparison ofCE-ASNBD, CEEMD and ASNBD

3 实验信号分析

为验证论文提出方法的实用性，论文将CE-ASNBD方法应用于轴承故障诊断。包络分析法能将与故障有关的信号从高频调制信号中解调出来，从而避免了与其它低频干扰信号的混淆，从而广泛地应用于轴承的特征提取[16-18]。论文对振动信号进行包络分析以提取轴承的故障特征。数据分为三类：可诊断(Y)、潜在可诊断的(P)和不可诊断的(N)。通过成功诊断被归类为不可诊断的数据集，可以证明算法的有效性[19]。

实验数据来源于美国西储大学轴承资料，试验台如图6所示，(实验平台包括一个2马力的电机(左侧)(1 hp=746 W)，一个转矩传感器(中间)，一个功率计(右侧)和电子控制设备(没有显示)，被测试轴承支承电机轴。使用电火花加工技术在轴承上布置了单点故障，故障直径分别为0.018、0.036、0.053、0.071、0.102 cm。其中前三种故障直径的轴承使用的是SKF轴承，后两种故障直径的轴承使用的是与之等效的NTN轴承。这个数据集的相关参数如表2所示。

图6 滚动轴承试验台图Fig.6 Rolling bearing test bench

表2 轴承数据信息表Tab.2 Bearing data information table

通过计算，可以获得数据集的故障频率。FE202的BPFO(球通频率，外圈)是105.87 Hz。BSF(球自旋频率)和FTF(保持架损伤频率)分别为59.69 Hz和11.42 Hz，分别用这三种方法分析记录FE202。原始信号和包络谱如图7和图8所示，从图可以很容易地推断出，只有四倍的旋转频率是清楚的，也就是4fr谐波清晰可见，而其他的频率信息是丢失的。原始信号被CE-ASNBD、ASNBD和CEEMD分解，分解结果和前四个组件的包络光谱在图7～图14中显示。fr谐波采用密集的点画线表示，而BPFO谐波采用稀疏点画线表示。

图7 截取的FE202信号图Fig.7 Intercepted FE202 Signal Diagram

图8 截取的FE202信号包络图Fig.8 Envelope diagram of intercepted FE202 signal

在CE-ASNBD分解后，在图9和图10中可以看到，谐波(fr，2fr，3fr，4fr)和BPFO谐波(BPFO，2BPFO，4BPFO)清晰可见，滚动轴承的外圈故障可以很容易且直观地感知。

而在ASNBD分解过程下，如图11和图12，虽然也能较为清晰的看见谐波(fr，2fr，3fr，4fr)和BPFO谐波(BPFO，2BPFO，3BPFO)，但在其后几个BPFO谐波频率中出现了缺失，以精确度来说，是不如改进后的CE-ASNBD方法。

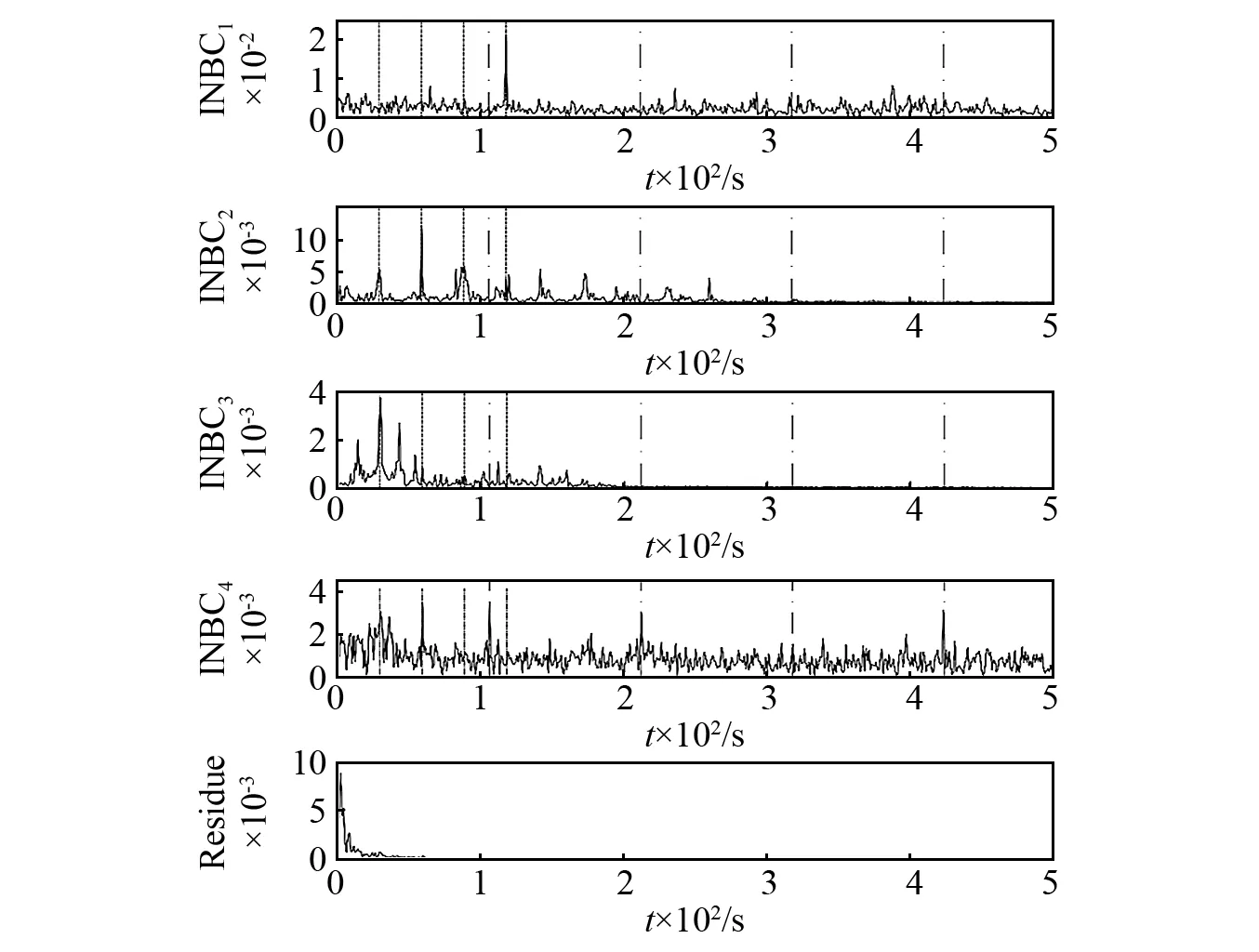
图10 FE202信号的CE-ASNBD的分解结果包络图Fig.10 Envelope diagram of the decomposition result of CE-ASNBD of FE202 signal

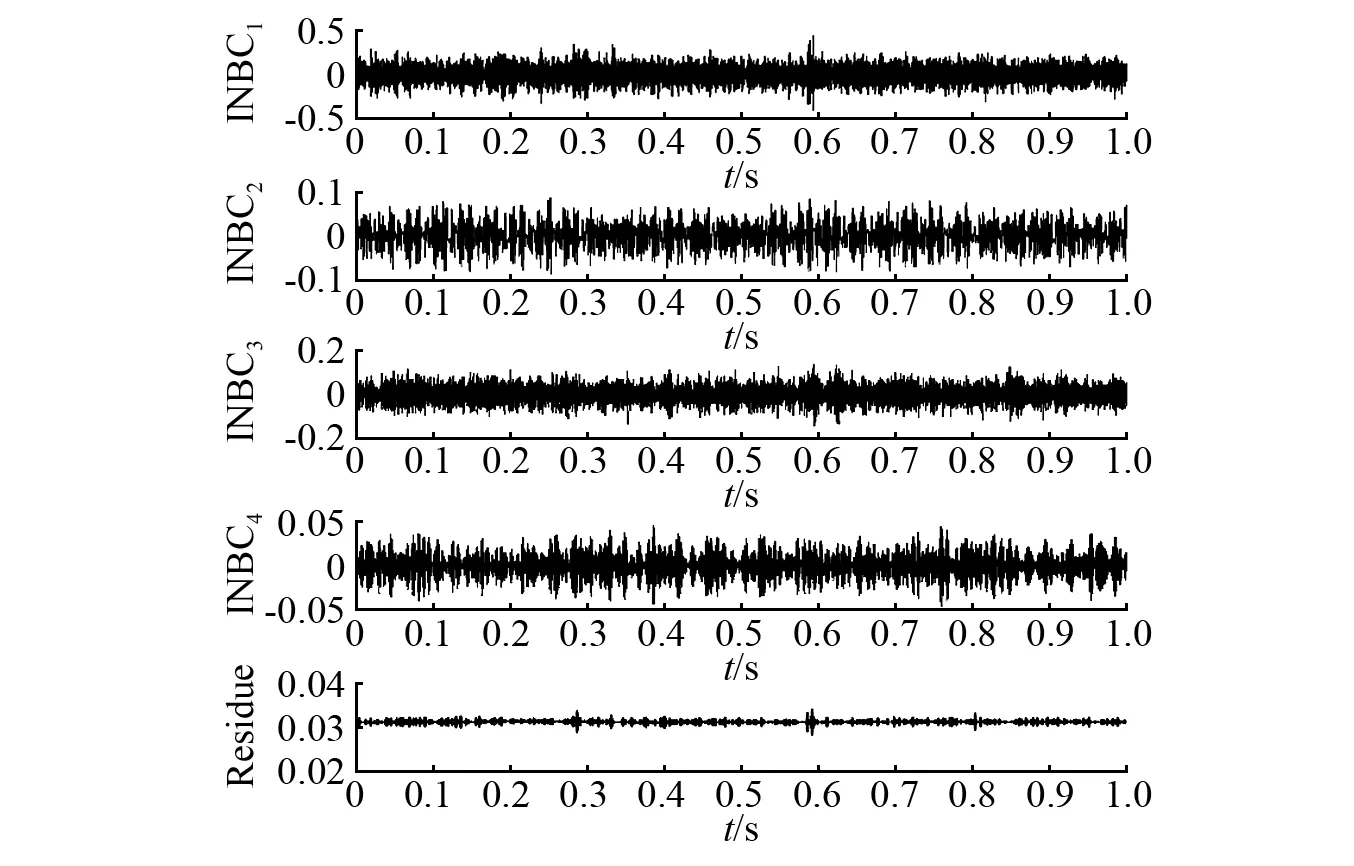
图11 FE202信号的ASNBD的分解结果Fig.11 ASNBD decomposition of FE202 signal

在采用CEEMD方法进行分解，如图13和图14，产生了大量的IMF分量。除了需要进行确认和辨别以外，包络图显示的旋转频率fr(fr，2fr，3fr，4fr)比较清晰，但BPFO谐波分量近乎完全缺失。

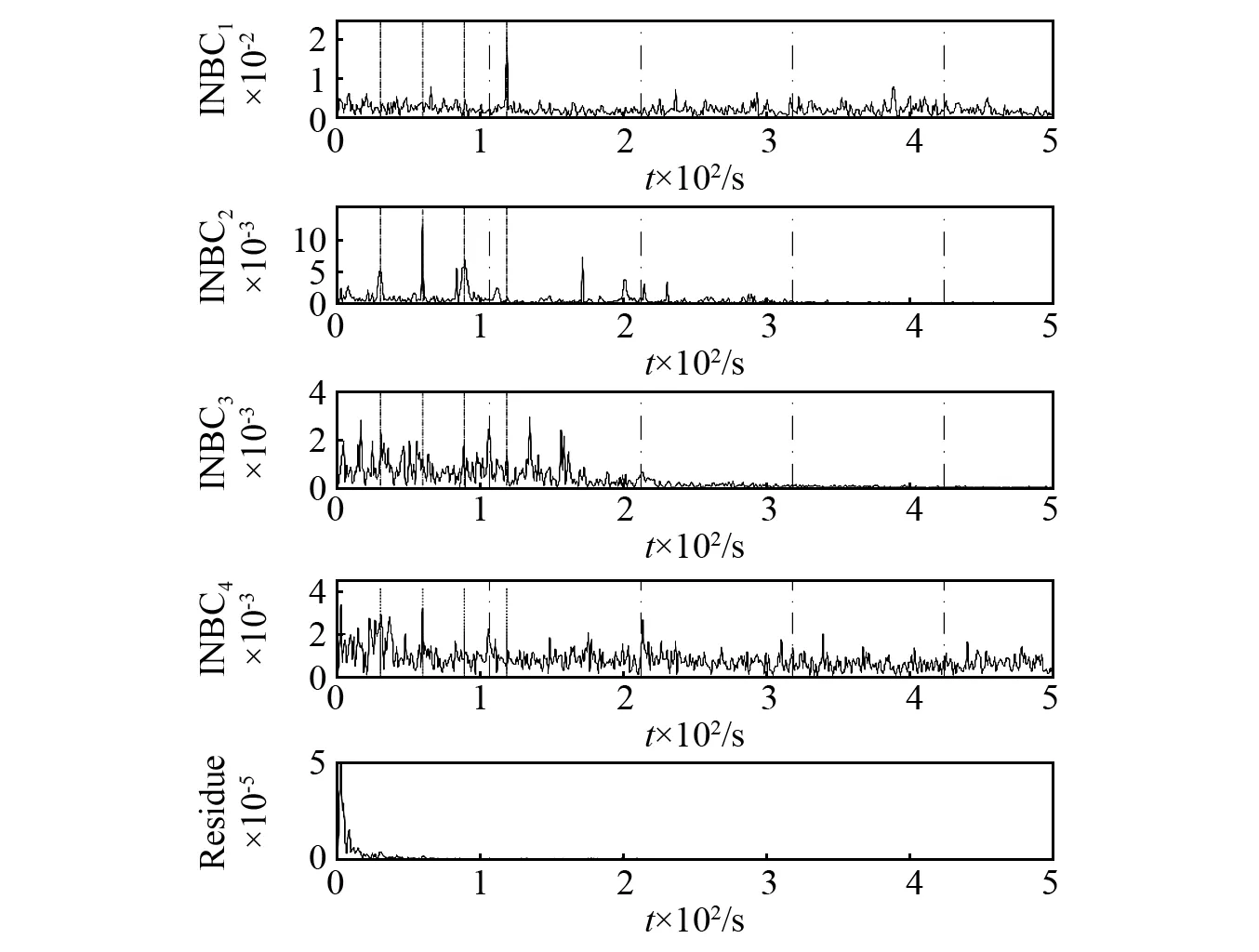
图12 FE202信号的ASNBD的分解结果包络图Fig.12 Envelope diagram of decomposition result of ASNBD of FE202 signal

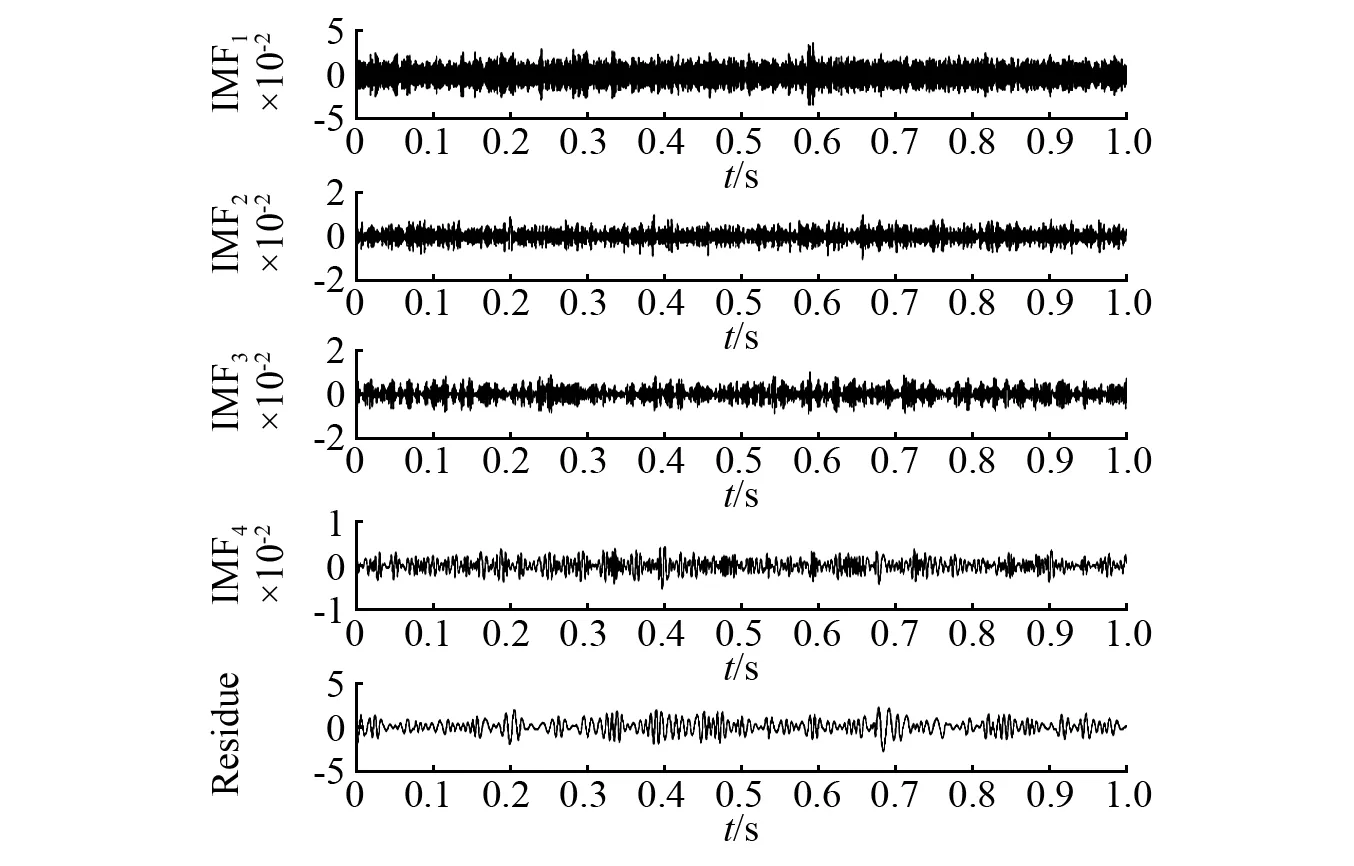
图13 FE202信号的CEEMD的分解结果Fig.13 Decomposition result of CEEMD of FE202 signal

图14 FE202信号的CEEMD的分解结果包络图Fig.14 Envelope diagram of the decomposition result of CEEMD of FE202 signal

上述分析结果表明，CE-ASNBD的性能优于ASNBD和CEEMD，用于非平稳信号。

4 结 论

ASNBD方法是一种新的自适应分解方法，可以用于非平稳、非线性信号的处理。为得到信号的最稀疏解，论文使用CE方法解决ASNBD方法中的优化问题。相对CEEMD方法和原本的ASNBD方法，CE-ASNBD方法具有以下优点：

(1)相对CEEMD方法，由于无须处理极值点，ASNBD方法分解出来的分量能有效抑制模态混淆，具有更好的准确性。

(2)相对原有的ASNBD方法，CE-ASNBD能更准确地得到全局优化值且具有较好的鲁棒性，因此CE-ASNBD方法分解得到的分量更接近真实值，且具有更好的抗噪声性能。

(3)仿真分析结果表明，相对ASNBD方法和CEEMD方法，CE-ASNBD方法分解出来的分量有更好的准确性和正交性，能更好的抑制模态混淆。

论文最后将CE-ASNBD方法应用于滚动轴承故障振动信号的故障诊断，对其做包络谱分析后提取了信号的故障特征频率成分，有效实现了滚动轴承的故障诊断，证明了该方法用于机械故障诊断的有效性。

值得一提的是，ASNBD方法刚被提出，在算法的多分辨率特性、计算效率、收敛性、优化算法的改进和奇异局部算子的选取等方面还需要进一步的研究。随着这些问题的深入研究，ASNBD方法拥有广阔的应用前景。