基于双树复小波的遥测振动信号多尺度噪声调节随机共振分析
刘 学, 孙 翱, 李 冬
(中国人民解放军91550部队,辽宁 大连 116023)
遥测振动信号是由安装在被试飞行器内的振动加速度或位移、温度、压力等传感器采集的反映系统运行状态的时间序列。受飞行器本身振动、飞行环境、电磁环境和传输条件等因素的影响,各结构部位的振动会相互影响、调制和叠加,振动的传输路径复杂多变,采集的遥测振动信号往往夹杂着大量的高频、低频和冲击噪声、各阶次的谐波分量,频谱成分异常复杂,且相关性耦合程度高,呈现较强的非线性和非平稳性[1]。
目前时频分析可以提供时间域与频率域的联合分布的多尺度信息,是当前非平稳信号分析的主要研究方向,很多自适应分解结合多尺度特征信息的分析方法相继被提出,如多尺度熵[2]、多尺度频带能量[3]、多尺度包络谱[4]等,虽然通过多尺度分析可以获得信号在不同尺度上的状态信息,但带内噪声对状态特征的影响并没有减弱。另外,目前的多尺度特征信息提取方法只是在不同尺度上分别研究分形维数、信息熵、能量、包络谱等特征信息,缺乏对多尺度信息联合应用,故不能揭示多尺度信息之间的内在联系。另外,自适应分解方法如经验模态分解(Empirical Mode Decomposition, EMD)、局部均值分解(Local Mean Decomposition, LMD)、局部特征尺度分解(Local Characteristic Scale Decomposition, LCD)等,其本身固有的模态混叠、端点效应以及伪分量等问题都会制约信号多尺度分解的效果。经Hilbert-Huang变换得到的瞬时时频谱虽然具有较好的时频分辨性和聚集性,但遥测振动信号频域成分异常复杂以及大量噪声的存在使得自适应分解方法产生严重的模态混叠现象,会造成混叠的时频分布覆盖整个时频平面,难以解读。
随机共振是一种利用噪声来增强信号的非线性信号增强方法,通过调节优化噪声类型和水平来驱动随机共振。但是在实际系统中的噪声强度很可能已经超过共振区域,由于受绝热近似理论和线性响应理论限制,随机共振理论的研究主要集中在小参数模型中,为了增强方法的实用性,国内外许多学者对大参数随机共振理论和方法进行了深入研究,可分为两类,频率转换和参数调节。频率转换类方法主要有频率调制技术,频率重采样技术和移频变尺度技术等[5-6]。但该类方法只能在频域进行,输出信号时域分辨率会降低。参数调节类方法采用尺度归一化、Woods-Saxon势阱等技术[7],虽然能够避免时域畸变问题,但是该类需要调节优化系统参数,复杂度较高,在微弱信号淹没在不同尺度噪声中的情况下性能很差。由于缺乏对信号中多尺度信息的综合考虑,对特征提取会产生较大影响。
针对上述问题,本文采用多尺度与非线性分析相结合的方法,实现优势互补,提出一种基于双数复小波的多尺度噪声调节随机共振分析方法,通过多尺度分析找准特征尺度带,然后采用非线性分析方法提取反映设备状态信息的敏感的状态特征。仿真和实测数据实验结果验证了该方法可以有效地对遥测振动信号进行分析。
1 参数调节随机共振方法
参数调节随机共振方法的双稳模型为[8]
(1)
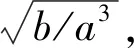
2 DTCWT多尺度噪声调节随机共振方法
系统状态异常通常表现得不是十分明显,反映在振动信号中则是十分微弱,为了进一步突出信号内在的非平稳和的非线性特性,还需对微弱状态信息进行增强,本研究基于以下3个结论展开:
(1)文献[11]研究表明带限噪声通过随机共振系统之后也呈洛伦兹分布;
(2)文献[9-10]通过大量的研究对比分析得出1/f型噪声相比其它类型的噪声在诱发驱动分量的随机共振效应方面有明显的优势;
(3)1/f型噪声可以通过正交离散小波变换(Discrete Wavelet Transform, DWT)获得[12]。
因此本文在参数调节随机共振方法的基础上,结合多尺度分析方法,将噪声类型转换为带限噪声,根据遥测振动信号噪声分布特点:信号中的驱动分量只存在于特定尺度上,而噪声在不同尺度均有分布,为了获得更好的随机共振效果,把各尺度噪声谱均调节成为近似1/f型,根据洛伦兹分布的特点,在频域上,多尺度噪声的能量将向驱动频率集中,残余噪声对故障特征频率也不构成干扰,进而可以提高系统的输出信噪比和处理色噪声问题。
2.1 双树复小波变换(DTCWT)
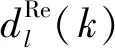
(2)
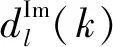
(3)
小波系数长度随着分解的层数而减半,为了得到与原始信号等长的分解结果,采用如下的小波系数单支重构算法
(4)
式中:m与n表示双树实部与虚部滤波器的长度。
2.2 双树复小波多尺度噪声调节方法
采用DTCWT作为多尺度噪声调节方法,充分利用其平移不变性、和良好的抗频带混叠和完全重构性等优良特性去构造频谱为1/f型噪声,DWT分解信号得到的小波系数dJ(k)是不相关的,其方差可表示为
var(dl(k))=δ2(2l)β
(5)
式中:σ2是与方差成比例的正常数;β是噪声的有色程度。白噪声的β=0, 1/f型噪声β=1。基于DTCWT多尺度噪声调节方法的具体步骤:
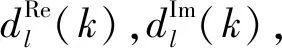
fs/2J+1≤fd≤fs/2J
(6)
(2)多尺度噪声调节:把多尺度信息调节为近似频谱为1/f型,根据式(4),调节方法为
(7)
(8)
式中:α=log2σ2为多尺度噪声调节中的调节参数,通过式(7)和(8)使得小波系数和尺度系数的方差满足式(5),即符合为1/f频谱形式
(9)
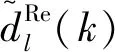
(10)
式(10)即本文提出的基于双树复小波多尺度噪声调节随机共振模型,该模型本质上也是参数调节类随机共振方法,区别在于新模型充分考虑了信号的多尺度噪声信息,将各尺度噪声谱均调节成为近似1/f型,且使得包含驱动频率的调节后的小波系数具有最大方差,而其余低频尺度的方差相对较小,根据洛伦兹分布的特点,在频域上,多尺度噪声的能量将集中向驱动频率集中。
2.3 樽海鞘群算法优化非线性随机共振
在获取多尺度信息时,受强非线性噪声的影响,一般很难将驱动信号从原信号中分离出来,在没有先验信息的情况下,驱动频率fd是未知的,因此最大分解层数J和多尺度噪声调节中的调节参数α很难确定,为了达到最优的随机共振效果,需保证小波系数中驱动力与噪声的强度比值在多尺度调节前后一致,针对这一问题,本文采用樽海鞘群算法去优化非线性随机共振。
2.3.1 樽海鞘群算法(SSA)
根据文献[14]提出的NFL理论,每种智能算法在解决不同的优化问题时的表现不尽相同,也就是说,不存在完全适用于所有优化问题的智能优化算法。经典的智能优化算法,如遗传算法、模拟退火算法等经常会存在后期收敛速度过慢,陷入局部极值的问题,此外,不同的智能优化算法所需控制的参数个数不同,控制参数过多不但会严重影响计算速度、稳定性,也大大提升了算法控制的复杂度。
最近文献[15]提出一种樽海鞘群算法(Salp Swarm Algorithm, SSA),算法模拟了深海中樽海鞘的群体行为,采用新的群体更新机制,每次迭代中,将群体进行排序,每个个体都紧紧跟随自己的前一个个体进行移动,而不是所有个体都只朝着最优值移动,这种模式大大的减少了陷入局部极值的情况。此外,SSA的控制参数少,在优化过程中仅需控制1个收敛因子,个体的运动与更新是根据观测空间的边界值进行控制的,降低了算法的控制难度,具有更快的收敛速度和较高的稳定性。文献[15]通过多个基准测试函数和工程应用验证了该算法性能。
(1)种群初始化
设捕食空间是一个N×D维的欧式空间,其中N为樽海鞘群的规模,D为空间维数。空间中存在食物F=[F1,F2,…,FD]T,樽海鞘的位置可以表示为Xn=[Xn1,Xn2,…,XnD]T(n=1,2,…,N)。搜索空间的上界表示为ub=[ub1,ub2,…,ubD],下界为lb=[lb1,lb2,…,lbD]。随机初始化种群:
XN×D=rand(N,D)×(ub-lb)+lb
(11)
(2)领导者位置更新
领导者负责在环境中搜索食物,引导整个群体的移动,因此领导者的位置更新要有很强的随机性,更新遵循公式(12):
(12)
式中:c2与c3都是[0,1]之间的随机数,作用是增强领导者移动的随机性,加强全局搜索能力与个体的多样性,c1这为收敛因子,它平衡算法在迭代过程中的探索与开发能力。当收敛因子大于1时,算法进行全局探索,迭代因子小于1时,算法开始对局部进行开发,得到精确的估计值。为了令算法在前一半的迭代中进行全局搜索,后一半的迭代中进行精确开发,SSA所取的收敛因子c1的表达式为
c1=2e-(4l/lmax)2
(13)
式中:l为当前迭代次数;lmax为最大迭代次数。
(3)追随者位置更新
SSA中,追随者不存在随机运动,而是呈链状顺次跟随移动,运动方式符合牛顿运动定律,因此追随者的运动距离R的表达式为
(14)
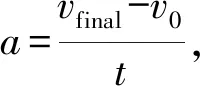
(15)
2.3.2 适应度函数选取
为了在先验信息未知的情况下使得驱动力、噪声和非线性系统达到平衡从而诱发驱动分量的随机共振现象,自适应选取最大分解层数J和多尺度噪声调节中的调节参数α,需要设计一个较好的优化指标,系统输出信噪比(Signal to Noise Ratio, SNR)是最直接的衡量指标,但实际情况下,由于驱动频率和噪声水平未知,该指标很难准确计算。功率谱峭度(Power Spectral Kurtosis, PSK)可以衡量频谱整体的尖锐度,其值随着信号信噪比的降低而减小,且谱峰越多、干扰谱峰的幅值越大,PSK值越小,因此,它与SNR在表征信号增强效果上具有相同的衡量意义,计算公式为
(16)
fitness=ρ×PSK
(17)
3 基于DTCWT的遥测振动信号多尺度噪声调节随机共振分析步骤
(1)首先对采集到的遥测振动信号进行零漂修正和趋势项消除;
(2)采用Hilbert变换提取振动信号包络;
(3)以式(17)作为适应度函数,采用SSA算法优化双树复小波的截止分解层数J和多尺度噪声调节中的调节参数α;
(4)采用2.2节的双树复小波多尺度噪声调节方法将不同尺度噪声频谱均调节为近似1/f型,重构信号;
(5)最后将重构信号输入到所提的随机共振系统模型,即式(10)中,得到增强后的驱动信号,对输出信号进行频谱分析,根据频谱中的最强频率,判断其是否接近于特征频率,进而得出分析结论。
4 仿真和实测信号分析
4.1 仿真信号分析
设置仿真实验,对经典的参数调节随机共振方法、基于DWT多尺度噪声调节随机共振方法和基于双树复小波多尺度噪声调节随机共振方法的性能进行对比测试。构造一个共振带中包含两个瞬态故障信息的振动仿真信号
x(t)=e-ζ[t-q1(t)/f1]sin(2πfrt)+ e-ζ[t-q1(t)/f2]sin(2πfrt)+n(t)
(18)
式中:fr为系统共振频率;f1和f2为故障特征频率;ζ为阻尼比;qi(t)=[t,fi](i=1,2);n(t)为高斯白噪声。
参数设置如下:fr=1 kHz,f1=100 Hz,f2=150 Hz,ζ=200 000,采样频率fs=12 kHz,仿真信号的信噪比SNR为-15 dB,仿真条件设置为观测范围为上界ub=[Jm,α=50],Jm由式(6)确定,下界lb=[J=1,α=1]的长方体空间,最大迭代次数50次,算法种群规模100。
仿真原始振动信号如图1所示,受瞬态故障低频信号的调制,波形表现为周期的衰减脉冲,从其频谱可以看出其共振频率为1 000 Hz,图2为通过Hilbert变换提取加噪后的信号包络,可以看出时域的脉冲特性和频域的共振带都被噪声所淹没,十分微弱,包络信号和其频谱中的瞬态故障频率完全被噪声覆盖,难以解读。
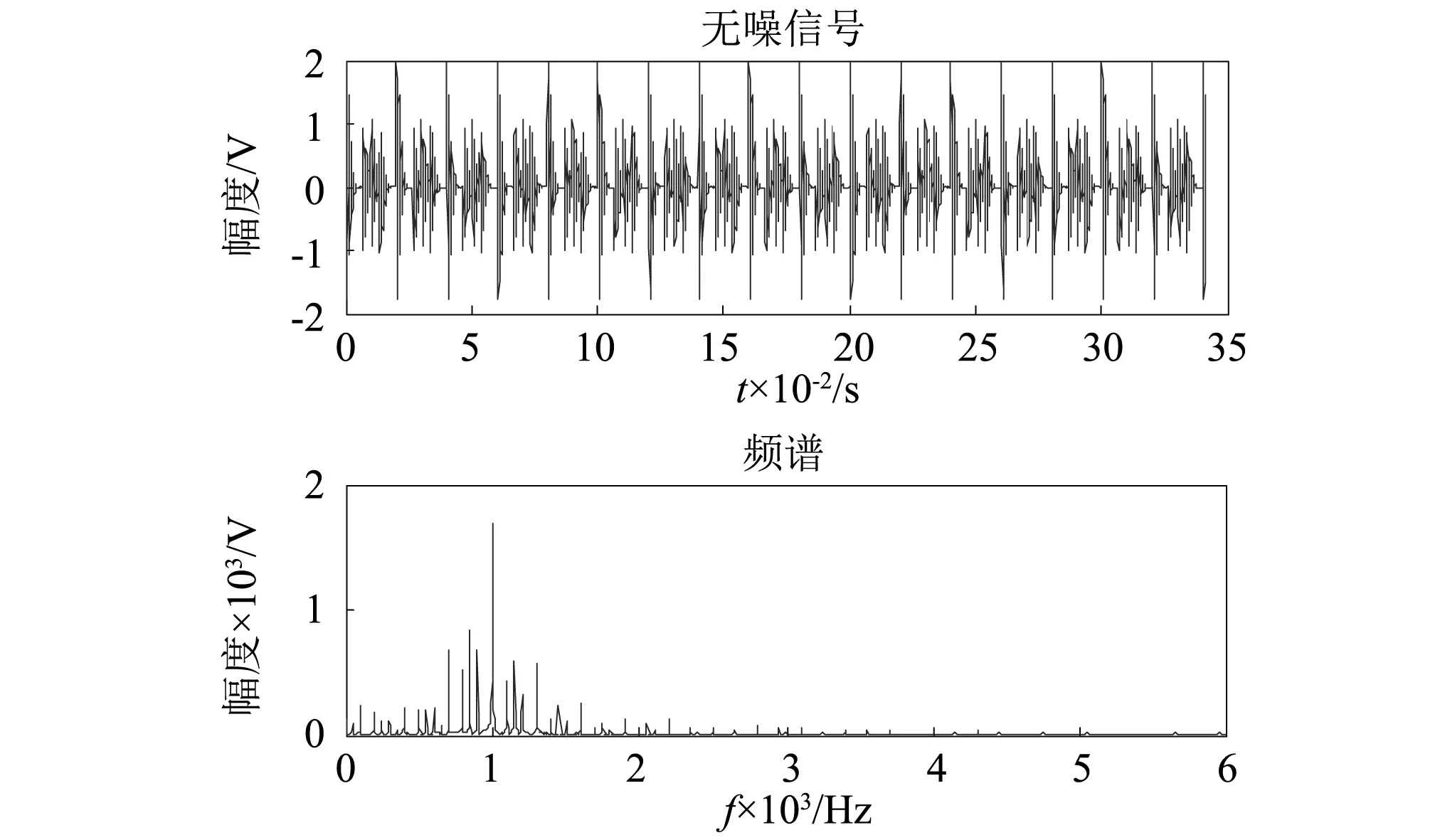
图1 无噪仿真信号及其频谱Fig.1 Waveform and spectrum of non-noise signal
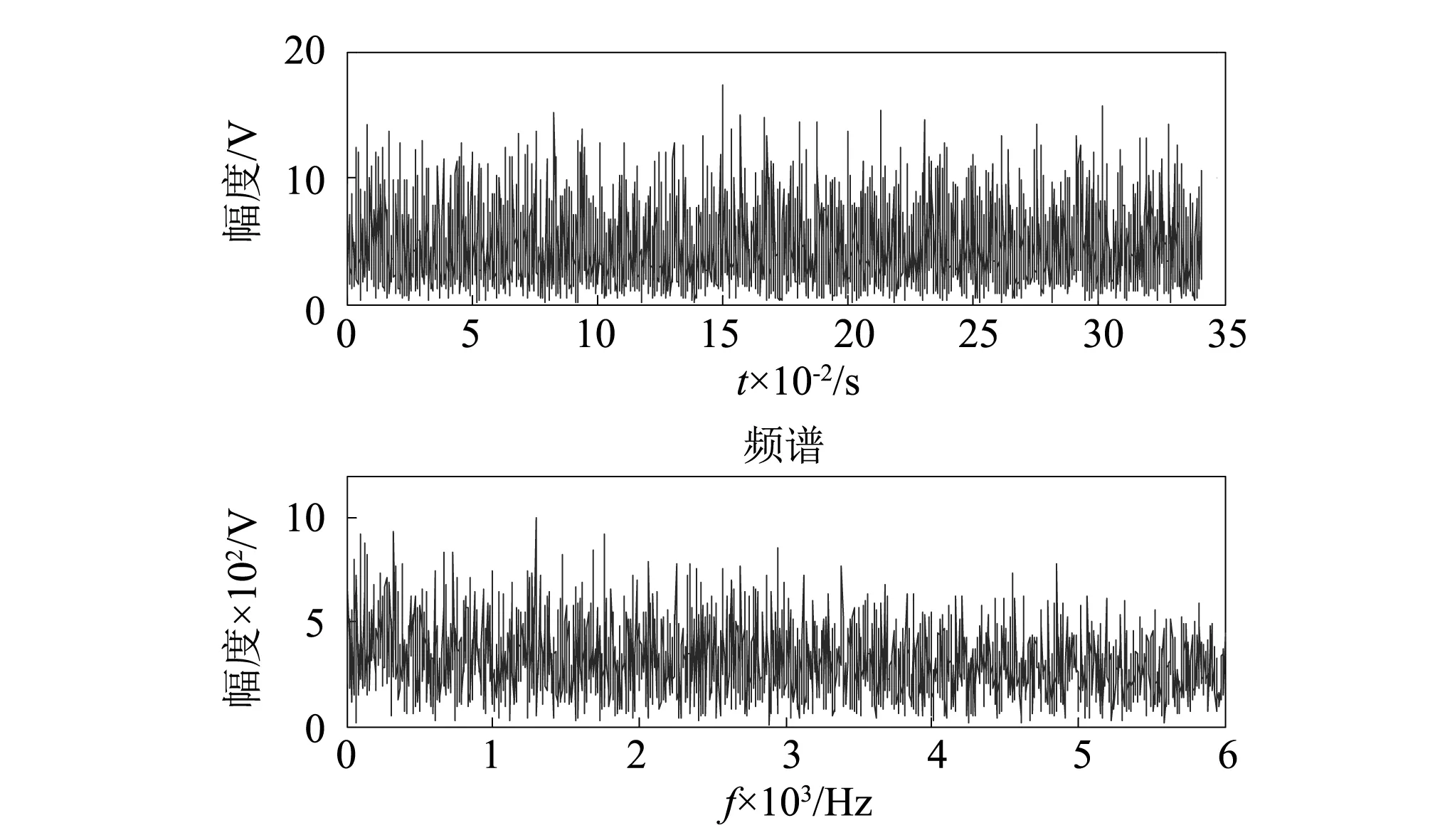
图2 含噪仿真信号包络及其频谱Fig.2 envelope and spectrum of the of noised signal
图3为经典的参数调节随机共振方法分析该包络信号的输出结果,比例因子,从图中可以看出,虽然该方法可以对信号的瞬态故障信息进行增强,但受到低频尺度噪声的影响,系统输出信号的频谱较为混乱,低频尺度噪声频率和故障频率相互叠加形成干扰,很难准确提取。
图4为基于DWT多尺度噪声调节随机共振方法系统的输出结果,最大分解层数J=6和调节参数α=16.2,从输出波形图就可以看到信号中存在周期成分,输出信噪比为-3.26 dB,两个故障特征频率100和150 Hz从输出信号频谱中较好地体现出来,解决了传统参数调节随机共振方法受低频尺度噪声干扰的问题。但DWT受制于频带混叠、平移改变等自身缺陷,在变换的过程中易引入干扰频率61.8和225.6 Hz,影响故障频率提取的准确性。
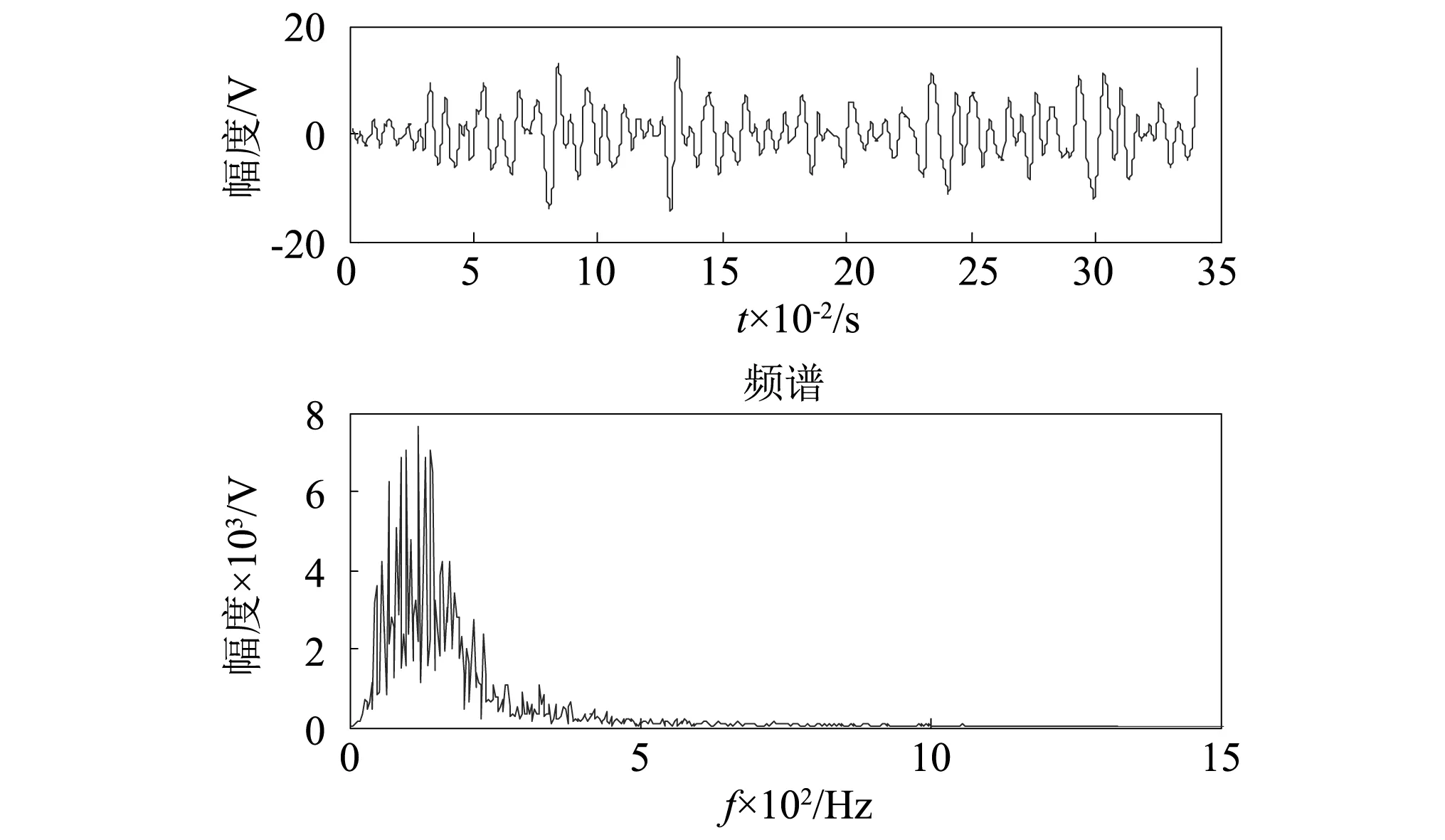
图3 参数调节随机共振系统输出Fig.3 Output signal of the parameter tuning stochastic resonance system
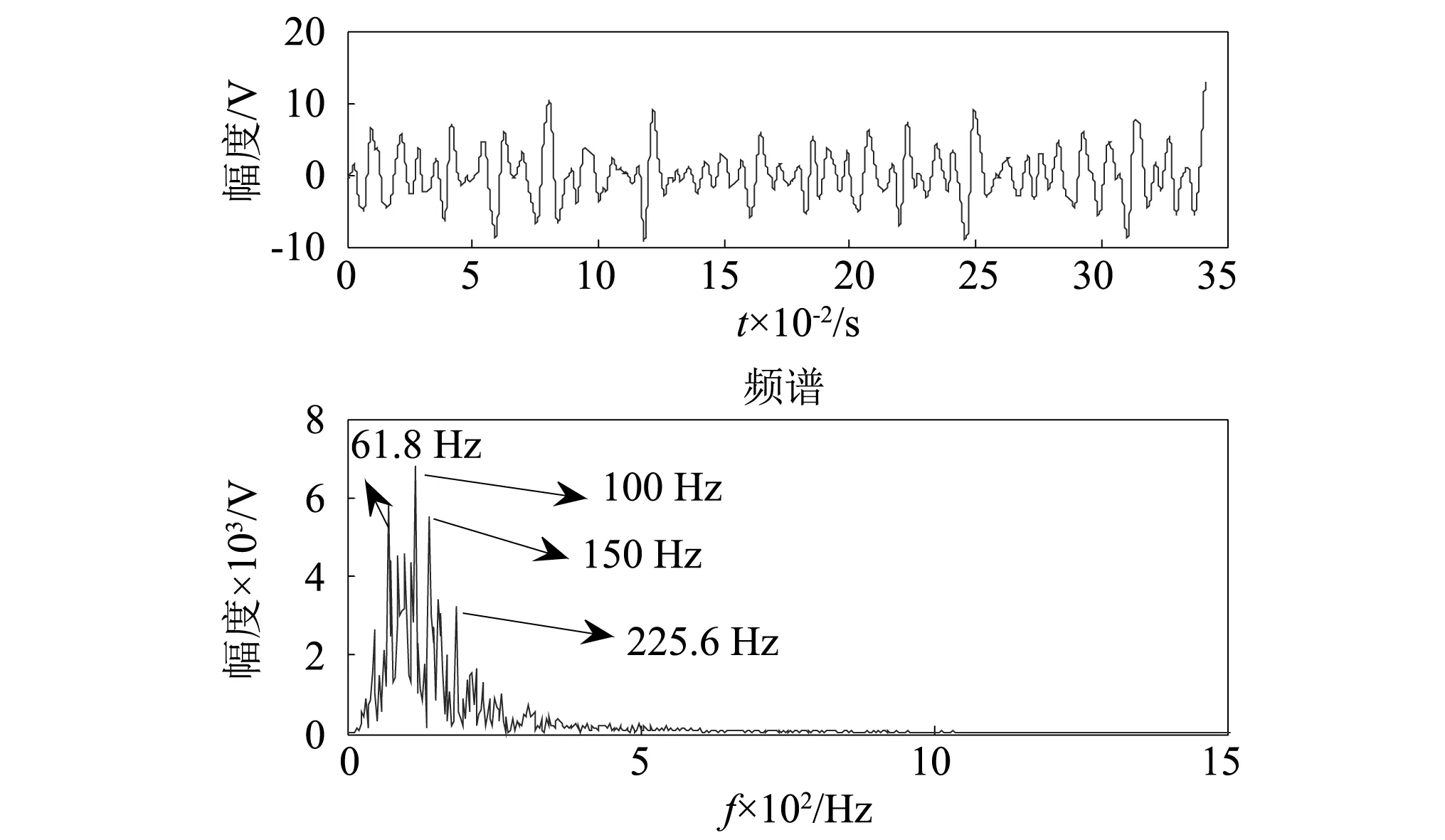
图4 基于DWT多尺度噪声调节随机共振系统输出Fig.4 Output signal of the multi-scale noise tuning stochastic resonance system based on DWT
SSA的迭代过程如图5所示,可见SSA迭代7次就很快搜寻到输出信号适应度的全局最大值432.74,得到的最优参数为J=6,α=18.4,图6为6层DTCWT分解,从图7基于DTCWT多尺度噪声调节随机共振方法系统的输出结果可以看出,故障特征频率在波形图和频谱中都占主导,输出信噪比为-0.83 dB,无干扰频率,从信噪比提升效果和故障频率提取的准确性两方面均优于其余两种方法。

图5 SSA迭代过程曲线Fig.5 Curve of the SSA iteration process
4.2 实测信号分析
采用某次飞行试验采集得到遥测振动信号对基于双树复小波多尺度噪声调节随机共振方法的性能进行检验,采样频率为5.12 kHz,SSA算法的观测范围为上界、下界、最大迭代次数和种群规模的设置与仿真实验相同,实测信号分析结果如下所示。
实测遥测振动信号如图8所示,时域的脉冲特性和频域的共振带都被噪声所淹没,无法进行分析,图9为基于DWT多尺度噪声调节随机共振方法系统的输出结果,采用SSA优化得到的最大分解层数J=7和调节参数α=33.7,从输出频谱图可以看到3个较为明显故障特征频率,分别为15.7 Hz,23.5 Hz和36.2 Hz,经与振动台试验结果对比分析得出,15.7 Hz为虚假频率成分,为DWT变换引入的干扰频率,剔除虚假频率计算输出信噪比为-4.28 dB。
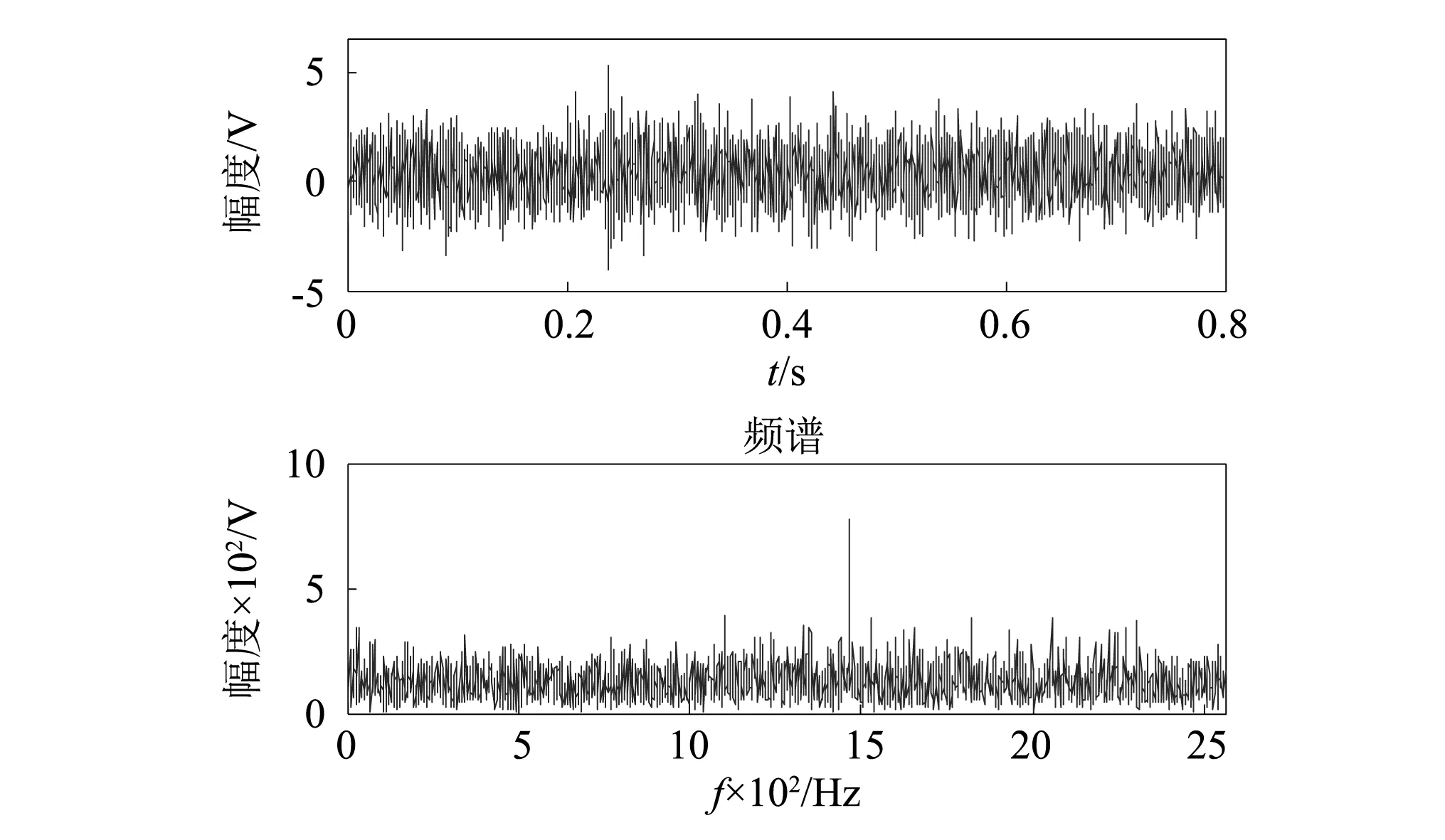
图8 实测遥测振动信号及其频谱Fig.8 Waveform and spectrum of telemetry vibration signal
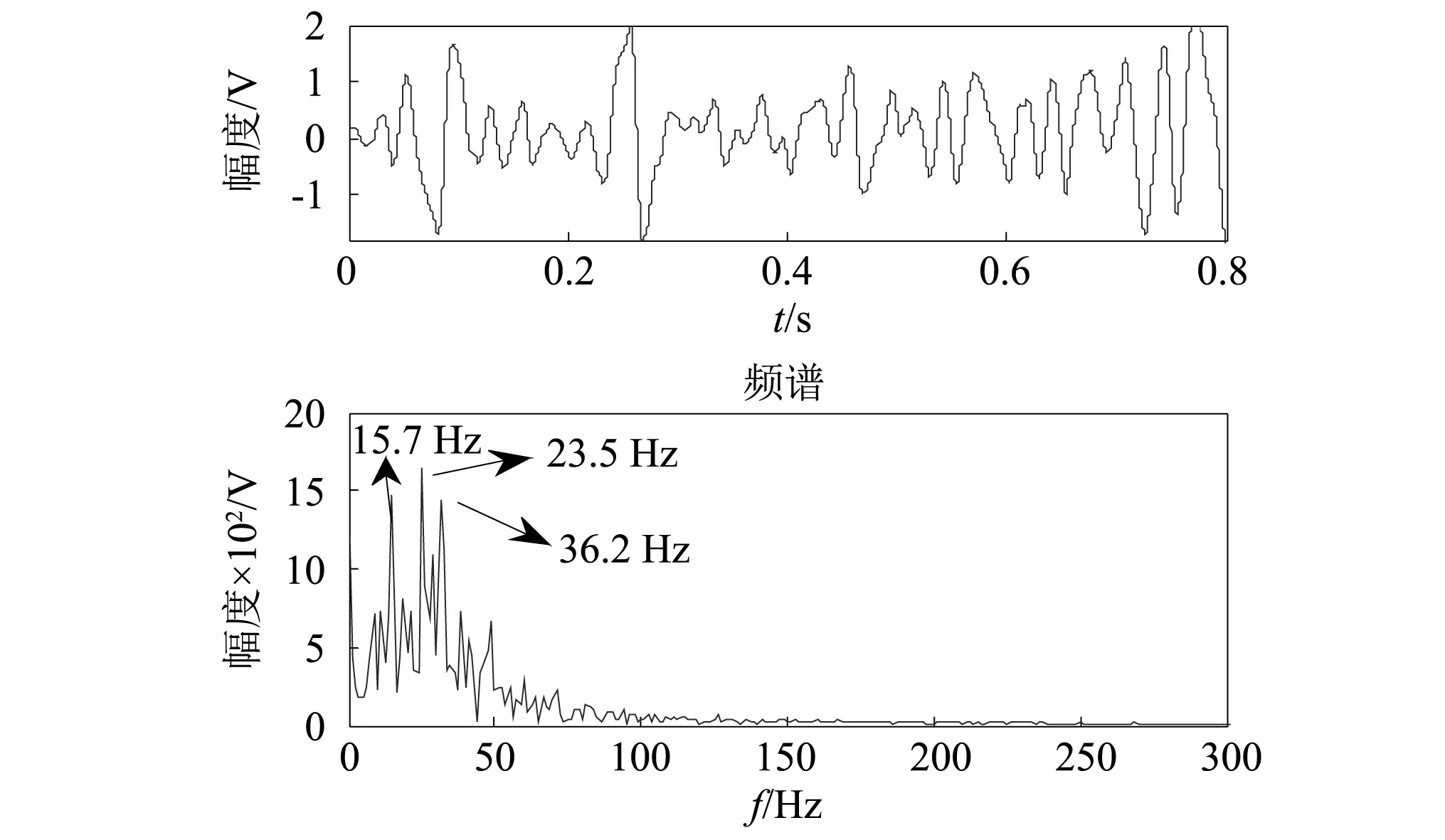
图9 基于DWT多尺度噪声调节随机共振系统输出Fig.9 Output signal of the multi-scale noise tuning stochastic resonance system based on DWT
基于DTCWT多尺度噪声调节随机共振方法的SSA需进行11次迭代搜寻到输出信号适应度的全局最大值511.2,得到的最优参数为J=7,α=35.2,图10为7层DTCWT分解结果图,从图11系统的输出结果可以看出,无干扰频率,输出信噪比为-1.66 dB,通过对实测信号分析表明,新方法从信噪比提升效果和故障频率提取的准确性两方面均优于其余两种方法。
新方法根据遥测振动信号噪声噪声在驱动信号包络谱的不同的尺度上均有分布的特点,采用DTCWT替代DWT把噪声类型和转换为带限噪声,把各尺度噪声谱均调节成为近似1/f型,避免了DWT因频带混叠、平移改变等缺陷,在变换过程中易引入干扰频率、驱动频率发生改变等问题,在频域上将多尺度噪声的能量向驱动频率集中,达到了对信号的瞬态故障信息进行增强的效果,因此性能更优。
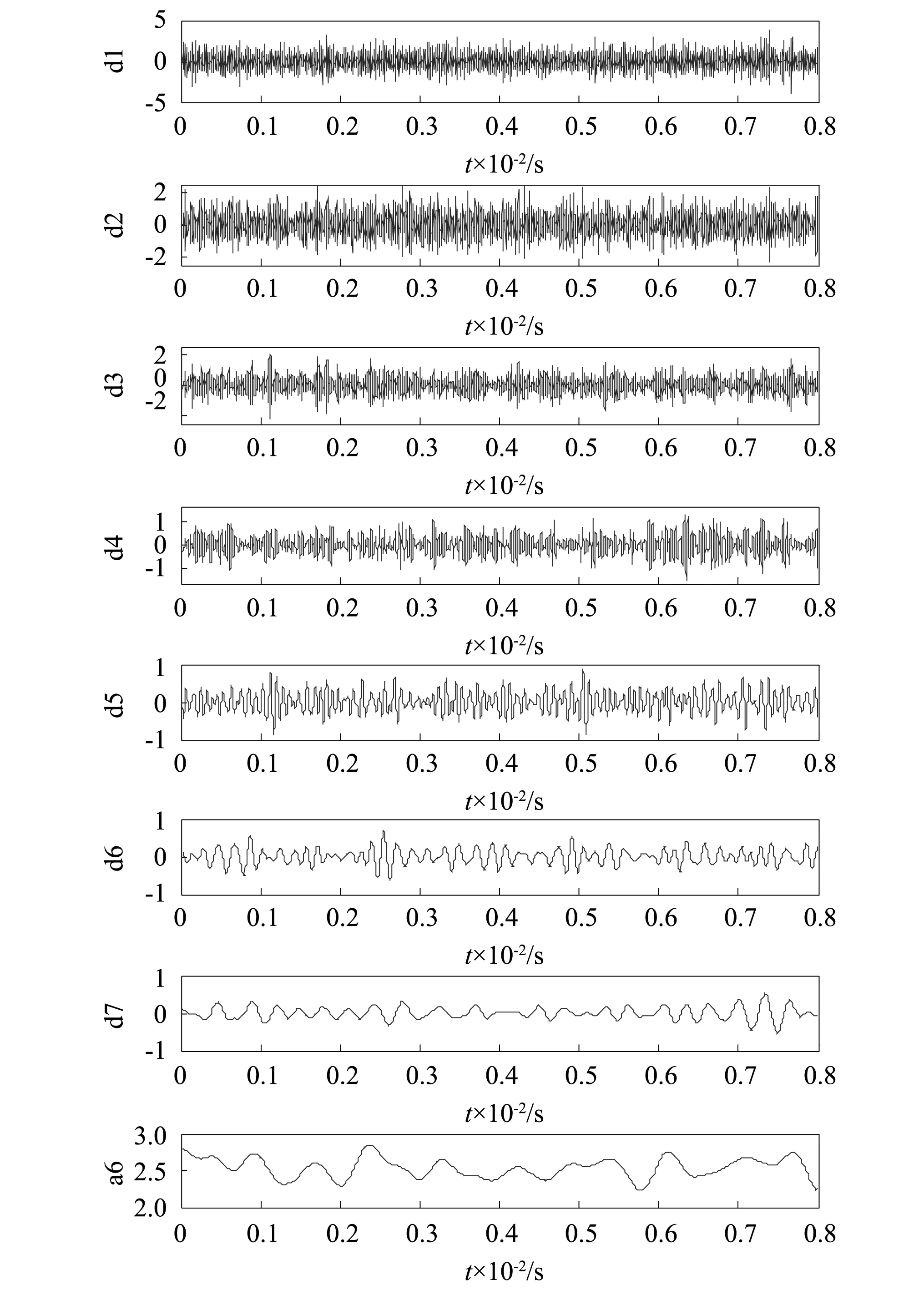
图10 7层DTCWT多尺度分解Fig.10 7 layers multi-scale decomposition of DTCWT
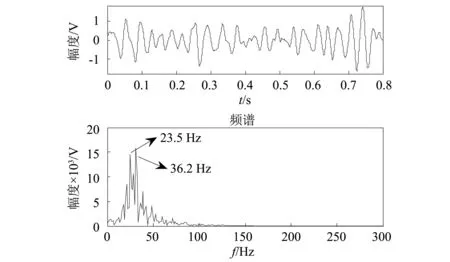
图11 基于DTCWT多尺度噪声调节随机共振系统输出Fig.11 Output signal of the multi-scale noise tuning stochastic resonance system based on DTCWT
5 结 论
提出了一种基于双树复小波多尺度噪声调节的随机共振方法,利用白噪声和带限噪声通过非线性随机共振系统后呈现洛伦兹分布这一特点,在先验信息未知的情况下,采用SSA进行自适应参数优化,通过对信号多尺度噪声类型和水平进行重新分配,将不同尺度上的噪声谱均调节为近似1/f型,进而使得噪声能量通过随机共振系统向驱动频率集中,达到提高系统的输出信噪比和处理色噪声问题,仿真和实测信号实验结果表明新方法的效果优于传统参数调节随机共振方法和基于DWT多尺度噪声调节的随机共振方法。

