基于轨迹段DBSCAN的船舶轨迹聚类算法

江玉玲, 熊振南, 唐基宏

(集美大学 a. 诚毅学院； b. 航海学院, 厦门 361021)

随着海上经济的发展，海洋运输已成为国内外货物运输的最重要方式之一，越来越多的船舶投入到海洋运输当中，沿海以及港口附近的船舶密度越来越大，船舶交通状况越来越复杂，这给船舶交管部门的管理带来很大的麻烦。船舶自动识别系统(Automatic Identification System， AIS)是获取船舶运动信息数据的重要手段。特别是国际海事组织(International Maritime Organization， IMO)通过的国际海上人命安全公约(International Convention for Safety of Life at Sea,SOLAS)修正案要求：所有300 t以上的国际航行船舶、500 t以内的非国际航行船舶以及所有客船，都必须强制安装AIS设备[1]，这使船舶监管部门可获取船舶数据。从AIS提取的船舶大数据中分析船舶的运动轨迹，对其进行聚类研究，从而得出船舶运动的规律以及进一步发现、分析船舶的异常行为，为海事安全监管和决策提供支持服务。

对运动物标的轨迹聚类，即将轨迹划分成不同的、具有相似运动规律的对象组成的子集。目前，国内外学者对轨迹聚类进行一系列的研究。吐尔逊等[2]采用DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法对模拟农业机械作业轨迹进行分析，对农机作业状态进行聚类分类研究，分析农机作业班次的有效作业轨迹、空行转移轨迹和停歇轨迹，得出农机利用率。周培培等[3]先基于速度的最小描述长度准则把轨迹简化成有序线段，再利用DBSCAN算法把线段分成不同的类，从而检测时空异常轨迹。陈锦阳等[4]利用特征点概念将轨迹分成轨迹子段，提出一种改进的轨迹子段距离度量方法，计算轨迹子段之间的相似度，用CTIHD聚类算法进行轨迹聚类。曹妍妍等[5]提出利用改进的Hausdorff距离进行轨迹相似度度量，然后采用谱聚类方法对距离矩阵进行聚类，从而得出符合实际的聚类结果。综上，这些专家学者在对轨迹聚类上都取得一定的成效，但是轨迹聚类应用于船舶AIS数据上的研究较少。本文针对Hausdorff距离可能存在的不足进行分析，结合船舶AIS数据的特点，提出一种利用船位转向角和航速变化量作为信息度量对船舶轨迹进行分段，把Hausdorff距离与离散Frechet距离结合作为轨迹相似度度量，基于轨迹段DBSCAN算法对运动轨迹进行分类，进一步获取船舶运动的典型轨迹，从而为研究船舶的异常行为打下基础。

1 船舶轨迹聚类的总体流程

基于船舶AIS数据实现轨迹聚类的总体流程见图1。

图1 基于AIS数据的轨迹聚类流程

2 AIS数据预处理

获取的AIS数据解码后存入数据库，首先要对数据进行预处理和清洗，这样才能得到有效的AIS数据。预处理的主要工作是清除信息表中呼号为0的数据；清除不同船舶但水上移动通信业务标识(Maritime Mobile Service Identification, MMSI)相同的数据；清除明显错误的数据，比如船位、速度或航向超过合理值的AIS数据。

3 轨迹聚类的实现分段

3.1 轨迹聚类方法研究

目前，国内外对船舶轨迹的聚类研究主要有两种方法。[6]

1) 把船舶的轨迹当作整体进行研究，这种方法可发现轨迹中的关键点，缺点是研究轨迹的开销大，而且会因为丢掉一些具有相似运动特征的轨迹子段[7-8]而失去一些重要信息，而这些重要信息对研究船舶轨迹至关重要。

2) 将船舶轨迹进行分段，分别对分段后的轨迹子段进行聚类研究，将相似的轨迹子段归类为簇,在此基础上再甄别异常的轨迹子段,从而有效地发现船舶的异常行为,为后期研究异常船舶轨迹打下基础。这种方法的缺点是无法保证船舶轨迹的完整性，但能具体研究轨迹子段的特征，以保证轨迹运动的重要信息不丢失，而且综合各轨迹子段后也能得到相对完整的整条轨迹[9-10]。

本文采用轨迹分段法进行轨迹聚类研究。

3.2 轨迹分段

对船舶轨迹进行分段处理，有保证原始轨迹信息的完整性和尽量保证数据的简洁性两个要求，即要求得到的子轨迹数量尽可能少，从而减少开销。

船舶运动轨迹示例见图2。船舶沿着P1—P8的实线运动。如果把P1点到P8点的所有点都采集下来当作船舶轨迹的关键点，保证了船舶原始轨迹的完整性，但是采样点多，计算复杂；如果只采集P1点、P5点、P8点3个点作为关键点，确实保证了采集点数量的简洁，但沿着P1—P5—P8的细虚线的船舶轨迹与原始轨迹对比，却丢失了原始轨迹的特征，不能保证运动轨迹的完整性：因而我们选择P1点、P3点、P5点、P7点作为采集的关键点，这样它们形成的轨迹P1—P3—P5—P7既能还原原始轨迹的特征，又具有一定的简洁性。

本文主要采用采集分段轨迹的特征点，船位转向角信息度量和船位航速信息度量两种方法。

3.2.1 船位转向角信息度量

船位转向角信息度量是通过设置特定船位的船舶转向角的阈值来实现的。船舶轨迹转向角指相邻几个船位所连接的两个船舶子轨迹段的航迹向之差。在给定距离D0范围内，P3—P4轨迹段和P4—P5轨迹段是船舶轨迹的两个子轨迹段见图3。这两个轨迹段之间的航迹向之差，也就是转向角为θ，将θ与设定的转向角阈值θmax进行对比，如果θ≥θmax则将P4点选为关键点，如果θ<θmax则继续采样，如此循环，直到遍历所有的点。

图2 船舶运动轨迹示例

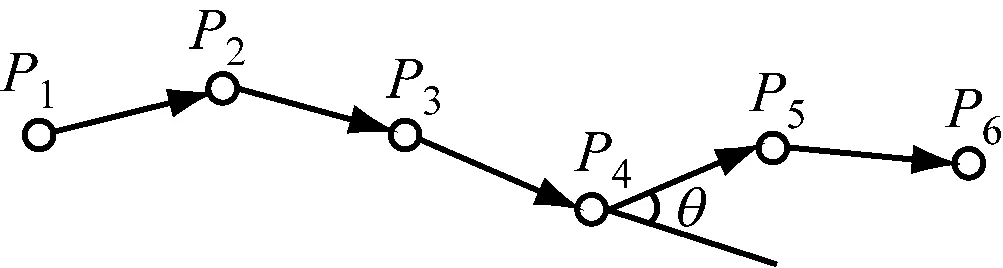
图3 船舶轨迹转向角

3.2.2 船位航速信息度量

轨迹设定一个给定的距离(dmin,dmax)，若在P3点的邻域距离(dmin,dmax)内，任意点与P3点的速度差的绝对值≥设定的速度阈值vmax，则不管P3点的转向角多大，都选定P3点为关键点，该点被称为变速点。

通过转向角与航速变化率来确定船舶轨迹的关键点，连接两个相邻的关键点，他们之间的连线就构成了船舶的轨迹子段。

3.3 轨迹相似度度量

度量轨迹间的相似性是实现轨迹聚类的基础，AIS数据中包含着丰富的船舶运动信息，如船位、航向、航速等，在轨迹相似性度量中要充分考虑这些信息。本文的轨迹子段包含船位转向角信息和船位航速信息，这能够提高聚类的准确度和分析效果。由船位转向角信息和船位航速信息确定的特征点组成船舶的分段轨迹。船舶的分段轨迹由一系列的特征点根据时间的先后顺序组成，其表达式为

TRi={Pi1,Pi2,…,Pij, …,Pin}

(1)

基于距离的相似度度量法有很多[7]，包括欧氏距离、Minkowski距离、余弦距离和Hausdorff距离等。最常用到的序列相似性度量的方法是Hausdorff距离：两条轨迹的距离越大，则轨迹间的相似度越低；反之，相似度就高。Hausdorff距离通常用来度量离散点集间的毗邻度，而船舶的运动轨迹被认为是矢量空间中有序的序列点集，考虑到两个序列即使有很小的Hausdorff距离，也并不能表示他们的相似度高，而且如果船舶运动轨迹点丢失，或者存在一个小的异常轨迹点，就会引起非常大的距离变化。针对这些问题，本文采用离散Frechet距离作为判别曲线间相似性的度量。

离散Frechet距离起源于人-狗距离模型，以函数的形式定义人-狗行进的两条曲线间的最小距离，将人与狗所行走的曲线抽象分别抽象为两个有序点串，从序列整体全局到局部细节逐级进行度量分析，避免Hausdorff距离分析只从点数据集合距离上判断各子目标相近程度的缺陷，整体态势上越接近，相似性越高[11]。

根据参考文献[12]，两者之间的离散Frechet距离表示为

(2)

式(2)中：假定{p1,p2,…,pn}为曲线P上的采样点，{q1,q2, …,qm}为曲线Q上的采样点；C={C1,C2, …,CK}为两曲线P、Q采样点连接的耦合距离集合；CR=(pi,qj)为欧氏距离，r=1,2, …,k,i∈{1,2, …,n},j∈{1,2, …,m}。

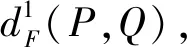
3.4 轨迹段聚类

轨迹聚类的方法有很多，本文采用基于密度的聚类方法。[13-14]传统的DBSCAN算法是最典型的密度聚类算法，他的对象主要是点，通过对比参考文献[9]、文献[10]、文献[15]、文献[16]发现，利用DBSCAN也可对轨迹段进行聚类，其研究方法与基于点的DBSCAN的聚类方法类似。其算法的主要思想是：将所有的轨迹段标记为未聚类的，读取轨迹段，通过ε和minLns判断该轨迹段是否是核心轨迹段。如果是，则该核心轨迹段的ε邻域形成一个新簇C并用该核心轨迹段标记。然后这个簇通过ε邻域的核心轨迹段不断向外扩展，直到簇不再增长为止。基于DBSCAN的轨迹段聚类法的相关定义如下：

定义1Li邻域的公式化定义为

Nε(Li)={Lj∈D|Ddist(Li,Lj)≤ε}

(3)

式(3)中：ε为轨迹段的密度半径；minLns为轨迹段的密度阈值；D为给定的轨迹子段数据空间；Li、Lj为轨迹子段。Li、Lj∈D,Li的邻域由所有与其空间距离不超过ε的轨迹子段构成。

定义2 对于Li∈D，如果Li的邻域满足

|Nε(Li)|≤minLns

(4)

则Li为核心轨迹段。

定义3 在数据空间D内，如果满足

Li∈Nε(Lj)

(5)

|Nε(Lj)|≤minLns

(6)

则Li到Lj是直接密度可达。

式(5)为轨迹子段Li在轨迹子段Lj的ε邻域范围，式(6)为Lj是核心轨迹段。

定义4 在数据空间D内，如果存在L1,L2,L3, …,Li, …,Ln(Li∈D,1≤i≤n),使得所有的Li+1从Li出发都是关于ε和minLns是直接密度可达的，则称Ln从L1出发是密度可达的。

定义5 存在一任意轨迹段Lk，Li、Lj、Lk∈D， 当Li和Lj都满足从Lk出发关于ε和minLns是密度可达，则称Li到Lj是关于ε和minLns是密度相连的。[17]

基于DBSCAN的轨迹段聚类算法流程见图4。

图4 基于DBSCAN的轨迹段聚类算法流程图

通过上述过程，直至遍历完所有的轨迹段对象，最终类C确定下来，DBSCAN算法示意见图5。在计算轨迹段核心对象时，将半径设为ε，密度阈值为minLns的外包椭圆作为搜索区域来获取，椭圆区域内包含的点为最终的类。

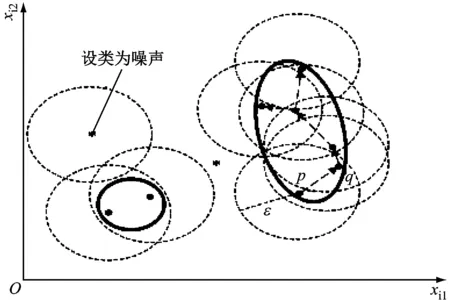
图5 DBSCAN算法示意

4 试验结果

本文以天津港获取的船舶AIS信息为研究对象对船舶轨迹进行聚类。选取天津港2016年8月1日—2016年8月3日的AIS数据，经过筛选和数据处理，显示出3 d船舶进出天津港轨迹见图6。3条航道从上到下分别是天津港主航道、大沽沙航道、大港航道，3 d的聚类轨迹分布在这3条航道上，总共198条船舶轨迹，轨迹某些段会重合，将3 d的船舶运动轨迹进行轨迹分段，获得951条轨迹子段。再利用轨迹段的DBSCAN算法对轨迹子段进行聚类计算，基于密度的DBSCAN算法对ε和minLns参数值的选定非常敏感[18]，试验需要反复进行。经过多番筛选，当ε=0.002 n mile，密度阈值minLns=3 时，聚类结果比较理想。

图6 3 d AIS船舶轨迹

为比较算法的优劣，对Hausdorff距离结合离散Frechet距离作为轨迹相似度度量的改进的DBSCAN算法与传统的Hausdorff距离作为相似度度量的DBSCAN算法进行比较，结果见表1。

表1 两种算法对比结果

由表1可知：基于离散Frechet距离作为轨迹相似度度量的改进的DBSCAN算法在运行时间上多于传统的DBSCAN算法，这是因为改进的DBSCAN算法需要利用船位转向角和航速变化量作为信息度量对船舶轨迹进行分段，相似性度量也较复杂，增加了计算的复杂度，但是该算法考虑船位转向角和航速变化量，并且能从多方面计算轨迹相似度，容易发现隐蔽的轨迹群，在分类结果和准确度方面优于传统的DBSCAN 算法。

试验再获取4 d、5 d的AIS船舶数据，利用改进的轨迹分段和轨迹段聚类算法对数据进行处理，得出轨迹分段后的轨迹子段数和聚类算法过程所用的时间。3 d、4 d、5 d的AIS船舶数据进行聚类算法的数据比较见表2。数据比较主要测试在执行聚类算法过程中，随着数据量的增加，其算法的执行效率。从试验结果来看，采用轨迹段DBSCAN算法，能较好地对船舶轨迹进行聚类，但此算法对ε和minLns参数值的选定比较敏感。而且由表2可知：随着数据量的增加，聚类过程所用时间基本成倍增加，所以在后期的研究中，需要关注在数据量增加的时候，如何改进聚类过程，节约聚类开销。

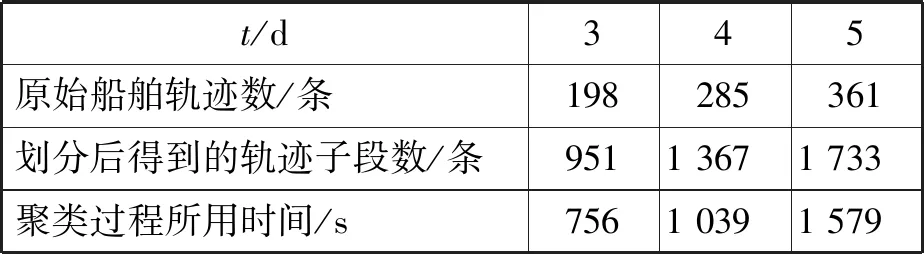
表2 3组AIS数据比较结果

为验证试验结果的可信度，从聚类后的船舶轨迹中求取船舶的典型轨迹。船舶的典型轨迹指的是将聚类后的各簇中的轨迹子段对应的船位、船舶速度、航向求平均值，每簇得到一条典型的轨迹子段，并将各轨迹子段按时间先后顺序相连得出的轨迹。取3 d的AIS船舶数据进行聚类，然后求其典型轨迹见图7，分别得出天津港主航道、大沽沙航道、大港航道的3条典型轨迹。图7中用3条点线表示提取出的典型轨迹，将船舶的典型轨迹与天津港3条航道设置相对比可知：船舶典型轨迹基本沿着航道的设置，由此可推断，试验结果可信，有一定的参考价值。

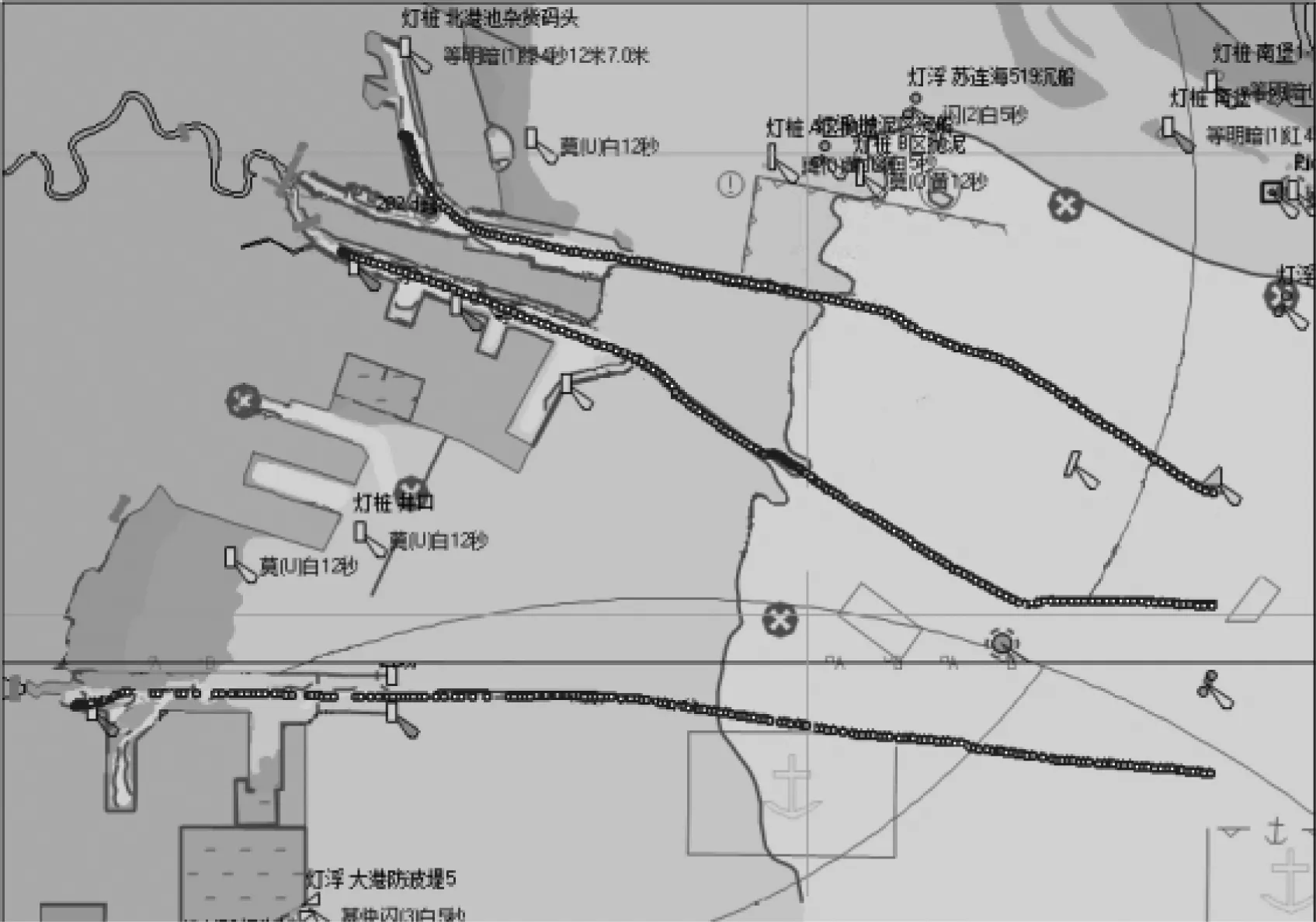
图7 船舶运动典型轨迹

5 结束语

本文基于船舶AIS数据，先对船舶轨迹进行分段，利用改进的轨迹段DBSCAN算法对轨迹子段进行聚类，对比改进的DBSCAN算法与传统算法的聚类结果，并得出船舶运动的典型轨迹。从对比试验结果看，改进的DBSCAN算法在聚类结果和聚类准确率上有所提高，并且船舶的典型轨迹能够按照天津港的航道设置。可将此试验数据作为参考，为进一步研究挖掘船舶异常轨迹打下基础。但从4 d、5 d聚类所需的时间看，随着分段轨迹数的增多，聚类所需时间成倍增加，怎样提高聚类效率也是后期研究的方向。