基于语义的船舶行为动态推理机制

文元桥, 张义萌, 黄 亮, 周春辉a,,c, 肖长诗,d, 张 帆,d

(武汉理工大学 a.国家水运安全工程技术研究中心； b.航运学院；c.智能交通系统研究中心； d.内河航运技术湖北省重点实验室，湖北 武汉 430063)

在复杂、开放的水上交通环境中准确地识别并预测动态、不确定的船舶行为是宏观、微观行为和异常行为分析的重点，其需要揭示船舶行为的行为模式和内在演化机制。在水上交通大数据中挖掘船舶的行为模式需要有效地组织水上交通态势信息，并清晰、完整地表达船舶行为的各个要素间的联系，发现船舶行为规律；揭示船舶行为的内在演化机制需要根据动态的信息发现各行为要素间的约束关系和影响程度，以在不确定信息中挖掘隐藏的船舶行为，并动态预测船舶行为。

在船舶行为相关研究中，刘敬贤等[1]定义港口内的汇入、汇出、穿越、掉头等船舶行为的概念。朱飞祥等[2]将港口水域划分为地理网格，并统计分析地理单元格上的船舶行为。甄荣[3]使用k-means聚类算法和贝叶斯分类器识别异常船舶行为。马文耀等[4]使用一致性检测识别船舶变速和转向异常行为。但目前国内的研究大多借用经典算法进行船舶行为分析，很少考虑船舶行为信息中要素与要素间的联系，因此难以形成背景信息与行为信息的交互机制，导致不能揭示船舶行为的内在演化模式并准确识别、预测船舶行为。

船舶行为要素与要素间的联系实际上是信息的语义描述及信息语义之间的关联关系，是构成语义网络的基础。语义网络是一种对某个领域中的概念和概念间关系建立明确、规范的形式化表达的模型，本体则是建立语义网络的建模工具[5]，而船舶行为语义网络是船舶的动作、行动以及对其所处交通态势的反应的语义描述与属性关系的集合。在近几年的研究[6-8]中，使用语义模型挖掘船舶行为已取得较好的成果。但使用语义网络自身的逻辑推理识别船舶行为难以处理船舶行为的动态性和不确定性。贝叶斯网络在给出不确定信息的推理结论方面应用十分广泛[9]，但其应用大多是静态贝叶斯网络推理，动态贝叶斯网络应用较少，面向海事领域的船舶行为动态概率推理研究更显缺乏。

1 问题描述与建模

为形成系统、清晰的船舶行为模型，揭示船舶行为的内在机理，挖掘隐藏的船舶行为，需要建立一种基于语义的船舶行为动态推理机制。从船舶的动态特性出发，以船舶轨迹为行为线索，构建船舶行为模型见图1。

图1 船舶行为模型

船舶轨迹实质上是时间序列下的位置点，考虑外界环境(包括基础设施、地理地形、气象水文等)的影响时，每个时刻的位置点都具有多维度的各种状态S(如航向、航速)；每种维度的连续位置点以及多种维度的多个位置点构成的不同层次的子轨迹段，分别表现为不同的船舶行为B(如加速)；多个不同层次的船舶行为以及状态可推理出事件E(如抵港)。每个时刻的状态、行为和事件互相耦合、互相影响，形成该时刻的船舶行为集合X，其表现为船舶行为规律约束的三维空间集合。某个时刻的船舶行为模型为

F(S(γ),B(γ),E(γ),σ)

(1)

式(1)中：γ={γ1,γ2,…,γn}为影响船舶行为的外界环境，如地点等，外界环境一般在一段时间内比较稳定，因此可作为船舶行为的参数。S={S1,S2,…,Sn}表示状态的集合，B、E类似。σ={σ1,σ2,…,σn}为状态、行为、事件间的相关函数集合。

船舶行为是随时间动态变化的，因此，需要引入时间序列t={t1,t2,…,tn}，在时间序列下的船舶行为模型为

G(Xt(γ),σ,δ)

(2)

式(2)中：Xt=St∪Bt∪Et为在时间序列t下的船舶行为集合，各个时刻的X表示的三维空间集合是随时间不断变化的；δ={δ1,δ2,…,δn}为船舶行为变迁函数集合，表示船舶行为在时间片间的变迁情况。

状态是最容易从原始数据中获得的，称为观测行为，而行为、事件为需要对船舶行为模型求解的隐藏行为。对模型的求解过程实际上是历史和当前时刻的状态已知时，在三维空间集合X内通过σ和δ等函数关系求当前时刻行为和事件的分布律，即

(3)

P(Et)=f2(S1:t,B1:t)=

(4)

使用语义模型清晰、完整表达出船舶行为的各个要素与要素间联系，得到行为模型F，并形成易于处理、易于表达的规范形式；使用动态贝叶斯网络基于语义模型深入挖掘隐藏的船舶行为，推理模型中的行为和事件，识别并预测动态船舶行为发生的概率，即构建在时间序列下的船舶行为模型G并求解P(Bt)和P(Et)。推理得到的行为概率可语义模型交互，形成动态的自然语言表达。

2 船舶行为语义模型

语义模型为某时刻的船舶行为模型，其对各船舶行为概念进行形式化表达，在非结构、无语义的原始数据中提取结构化的语义信息，构建以船舶行为为核心的语义网络(见图2)。

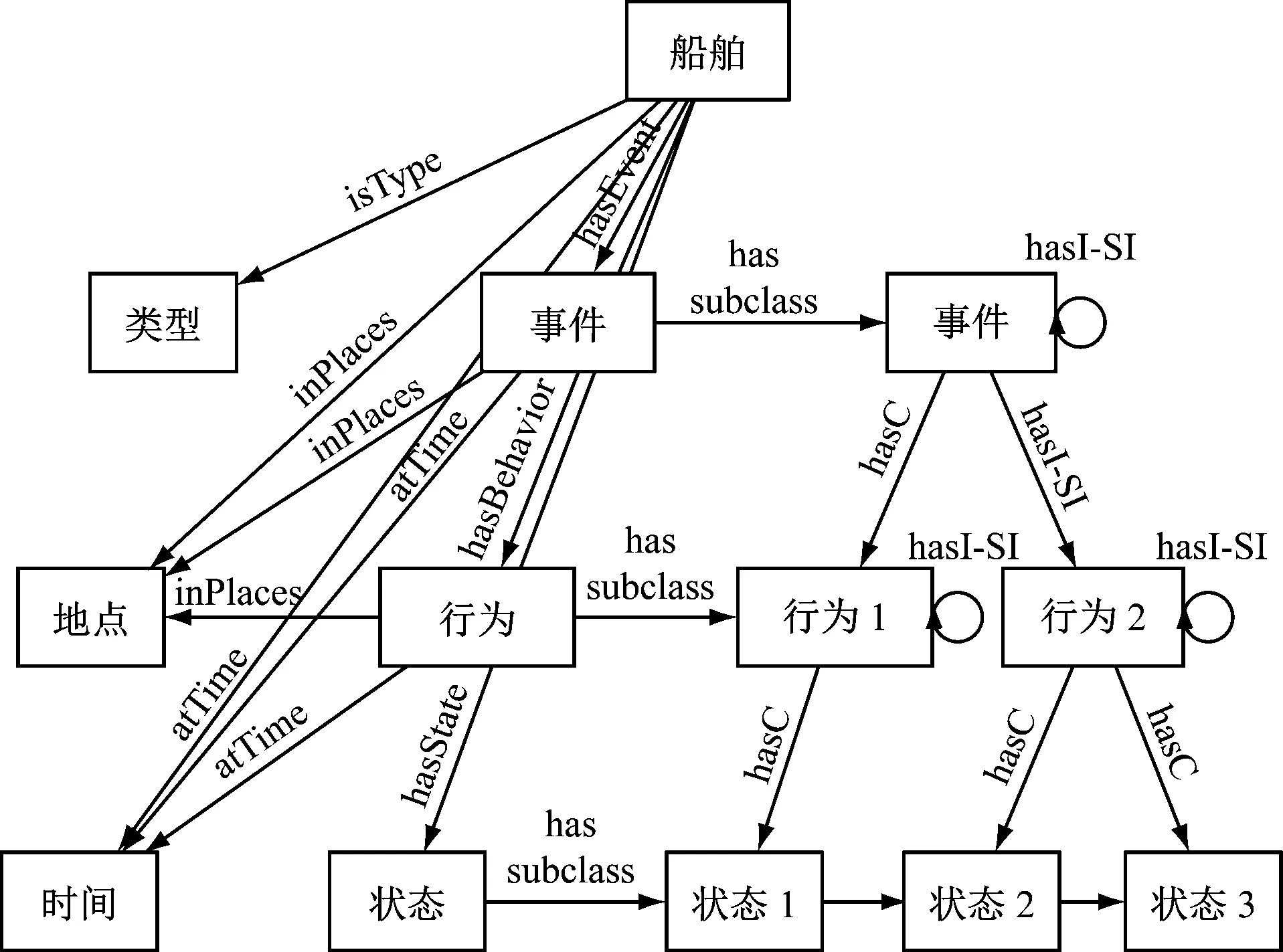
图2 船舶行为语义网络模型

语义网络可以形式化表达为一个三元组：

SN={C,R,I}

(5)

式(5)中：SN为语义网络；C={C1,C2,…,Cn}为类，他表示对象的集合，包含船舶行为集合X和外界环境γ；R={R1,R2,…,Rn}为关系的集合，表示类之间的相互作用，包含相关函数和变迁函数δ；Ii为本体的实例，也就是具体的对象。具体而言，C={V,P,T,Tp,S,B,E}，其中：V、P、T、Tp分别为船舶(Vessels)、地点(Place)、时间(Time)和类型(Type)，S、B、E即上述提及的状态(State)、行为(Behavior)、事件(Event)，此3类为核心类。

语义模型中关系集合包括对象属性(Object Property)和数据类型属性(Data Type Property)。数据类型属性为类或个体的数据描述或数据限制，如船舶A速度为10 kn，高速船舶船速最低为15 kn等。对象属性包含以下类间的关系：

1) Vessels类与atTime、hasBehavior、hasEvent、inPlaces、isType其他类的属性关系等。

2) Behavior类和Event类与Time类的atTime属性关系，动态贝叶斯网络推理后的结果以开始时间和结束时间在语义网络中存储，以便于查询、调用和表达。

3) State类、Behavior类、Event类之间的hasCharacteristics(简记为hasC)和hasInter-SliceInfluenceto(简记为hasI-SI)属性关系，hasCharacteristics属性关系为某时间片内的节点间关系，hasInter-SliceInfluenceto为相邻时间片的节点间关系，分别对应船舶行为模型中的相关函数和变迁函数δ。

语义模型中类的实例(Instances)为类的实际对象，如船舶的实例渡船江城4号(JiangCheng4Hao，MMSI:413932547)等。

3 船舶行为动态贝叶斯网络模型

3.1 动态贝叶斯网络定义

动态贝叶斯网络的初始网络和转移网络见图3。

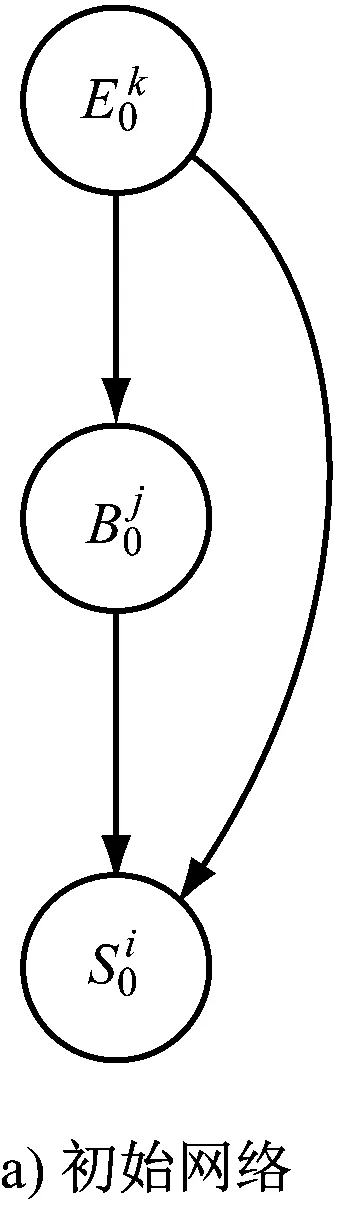
图3 动态贝叶斯网络的初始网络和转移网络

1) 在t=0时间片，将语义网络转化为初始网络，并定义初始时刻的概率分布P(X0)。其基本思想是将语义网络中属于状态、行为、事件的子类对应贝叶斯网络中的节点，节点对应随机变量Xi，其概率值为P(Xi)；子类的实例对应随机变量Xi的取值，本文中的取值都是离散的；子类间的属性关系对应节点间的有向弧，表明节点间的直接影响，并具有相应的条件概率。在初始网络内的所有节点的联合概率可表示为

(6)

式(6)中：Pa(Xi)为任意Xi节点(i=1,2,…,n)的所有父节点。若Xi没有父节点，则Xi为根节点，P(Xi|Pa(Xi))=P(Xi)表示其先验概率。

2) 在t>0时间片的节点可能受以前时间片内节点的影响，另外可由上一时间片节点的概率预测下一时间片节点的概率，所以需要定义转移网络。假设动态贝叶斯网络符合一阶马尔可夫过程，则转移网络为包含两个相邻时间片的贝叶斯网络。时间片间仅有行为或事件节点间的影响，可定义Zt为t时间片贝叶斯网络中的所有行为节点(Bt)和事件节点(Et)，则第t个时间片的Zt在之前所有时间片下的条件分布为

P(Zt|Z0:t-1)=P(Zt|Zt-1)=

(7)

P(St|Z0:t-1,S0:t-1)=P(St|Zt)

(8)

由初始网络和转移网络可将动态贝叶斯网络展开到第T个时间片。从第0个时间片到第T个时间片的联合概率分布为

P(X1:T)=P(Z0)·P(S0)×

(9)

3.2 参数学习

初始网络中的条件概率和转移网络中的转移矩阵分别对应船舶行为模型中的相关函数σ和变迁函数δ，两者都为动态贝叶斯网络中的参数θ，需要在推理前给出。本文使用最大似然估计法进行参数学习。动态贝叶斯网络中的节点都为离散型随机变量，设其分布律为

P{X=x}=p(x;θ),x=x(1),x(2),…

(10)

式(10)中：θ=(θ1,θ2,…,θm)T为未知参数。(X1,X2,…,Xn)T为来自总体X的样本，则样本的联合分布律称为似然函数，记为L(θ)，即

(11)

之后，选取使似然函数达到最大的参数值作为未知参数θ的估计值，即求似然方程：

(12)

3.3 动态推理

(13)

贝叶斯公式

(14)

由式(14)和贝叶斯网络的条件独立性假设可得

(15)

4 实例计算与结果分析

为对上述模型进行验证，选取所有船舶共有的靠离泊行为为例进行实例分析。具体验证过程如下：

4.1 基础数据处理

使用的数据来自于船舶自动识别系统(Automatic Identification System，AIS)和谷歌地球，AIS数据为长江渡船江城4号于2014年1月1日某航次数据，地理数据为武汉关码头区域数据。对AIS数据进行抽取和清洗等预处理后，仅需要对轨迹数据和地理数据做简单的判断即可得到状态信息，如加减速状态仅需要判断AIS数据中的速度是否增加等。判断转向状态时航向差Δcog(cog为船舶对地航向)计算为

(16)

4.2 靠离泊语义网络建模

语义网络见图4(图中部分概念后的英文为语义概念简称，同时省略图2中已有的属性关系)，其中：转向行为(Turning)由前5个轨迹点的转向状态(turn1-5)推理；变速行为(SpeedChange)与转向行为类似；停泊行为(Berth)由在港内/外(inside/outside)和速度是否为0(speed=0)推理；驶入/驶出行为(Enter/Leave)由相邻两点是否在区域内的状态判断；抵港/离泊事件(Arrival/Departure)由变速行为和是否在码头区域内推理；横驶事件(AcrossRiver)由离泊进行预测，指离开码头区域后渡船横渡长江的行为，其没有证据支持判断，只能由渡船的行为模式为依据，根据离泊和其本身预测，因此可检验模型的预测能力。

4.3 动态贝叶斯网络构建与参数学习

语义网络与贝叶斯网络都是图结构模型，其中：语义网络中的类可转换为贝叶斯网络中的节点;类下的实例可以转换为节点下的变量;类间的属性关系可以转换为节点间的依赖关系[10]，且只需对状态、行为、事件3层需要动态推理的核心类进行转换。由语义网络得到的靠离泊动态贝叶斯网络见图5(各节点简记为英文首字母)。

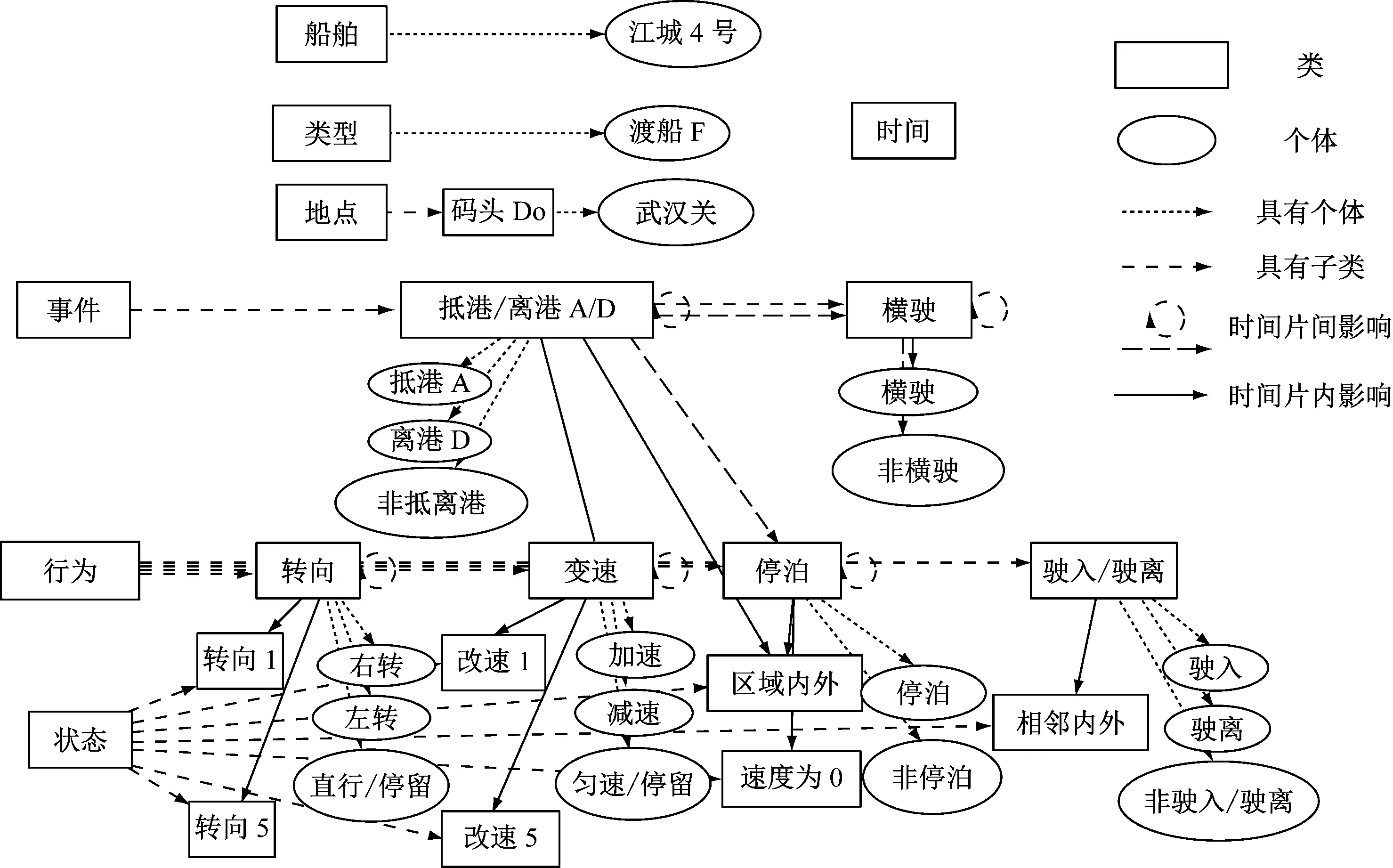
图4 靠离泊语义网络

得到网络结构后对该渡船2014年1月的AIS数据(约27万条)标注，作为参数学习样本。使用最大似然估计的方法进行参数学习，得到概率见表1～表3(部分概率表省略)。

图5 靠离泊动态贝叶斯网络

表1 边缘概率

表2 时间片内条件概率

4.4 推理并预测船舶行为

已知网络结构和参数后，结合由数据得到的状态节点概率，即可动态推理船舶行为和事件发生的概率，江城4号靠离泊轨迹见图6a，推理结果见图6b～6d。由于停泊时各行为的概率变化很小，图6省略了部分停泊时间片的推理结果。

由图6可知：抵港、离港和停泊都与事实相符，且船舶在抵港时减速左转，离港时加速，符合良好船艺。模型不会像逻辑推理一样将可能发生的行为误判为没有发生，而是赋予该行为准确的发生概率。时间片间的转移矩阵使得行为的判断不仅依赖于当前时间片内的证据，还考虑历史行为的影响，因此，当前时间片内的证据不准确时不会出现行为误判。

推理结果中加粗线段(停泊和横驶)为明显进行了行为预测的部分，其中：在抵港将要结束时(11≤TS<16)停泊被预测出将要发生；而横驶初始概率即为其边缘概率，之后其发生的概率受历史时间片中离泊和其自身发生的概率影响，在离泊发生后(49≤TS<53)其发生的概率逐渐增大，尤其是在离泊概率降低时(TS=52)，横驶概率达到最大，表示其将要发生。但由于没有证据支持，在离泊结束后(TS≥53)横驶逐渐趋向于其本身的边缘概率。由于预测行为不是由证据直接推理所得，而且有实际发生的行为的限制，其概率较小，因此能够与实际发生的行为相互区分。

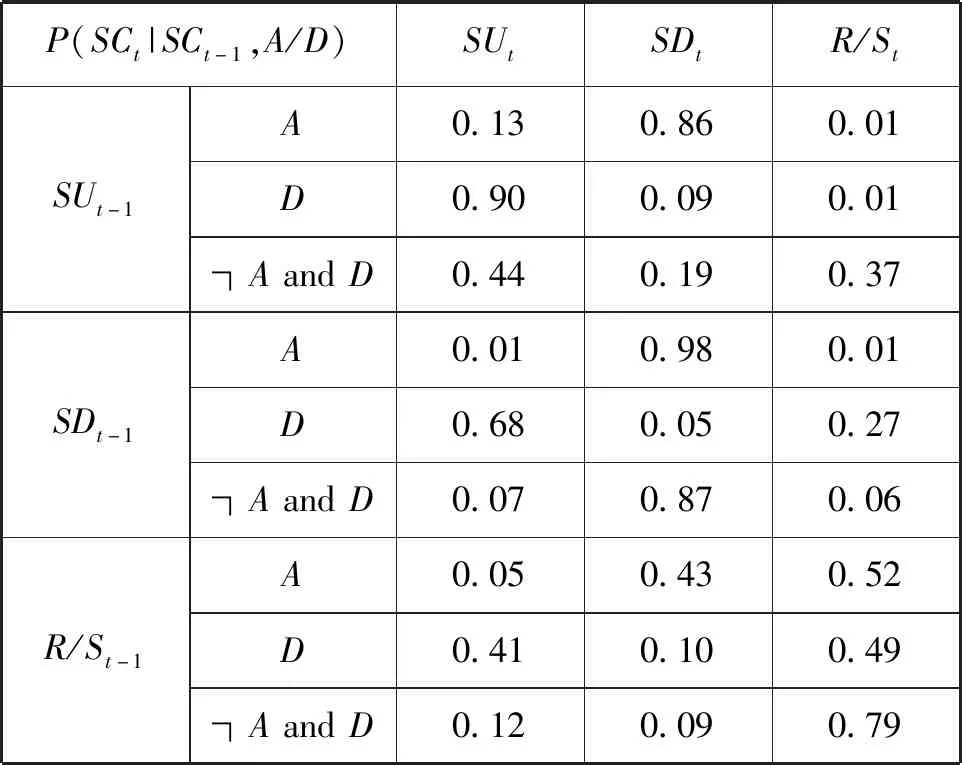
表3 时间片间转移矩阵

推理结果既可用概率曲线形式描述，也可映射到语义网络中，以方便船舶行为的语义化表达和进一步的共享、查询等应用。当行为将要发生或已经发生时进行简单的语义组织即可形成如下语义表达：

a) 江城4号靠离泊轨迹图

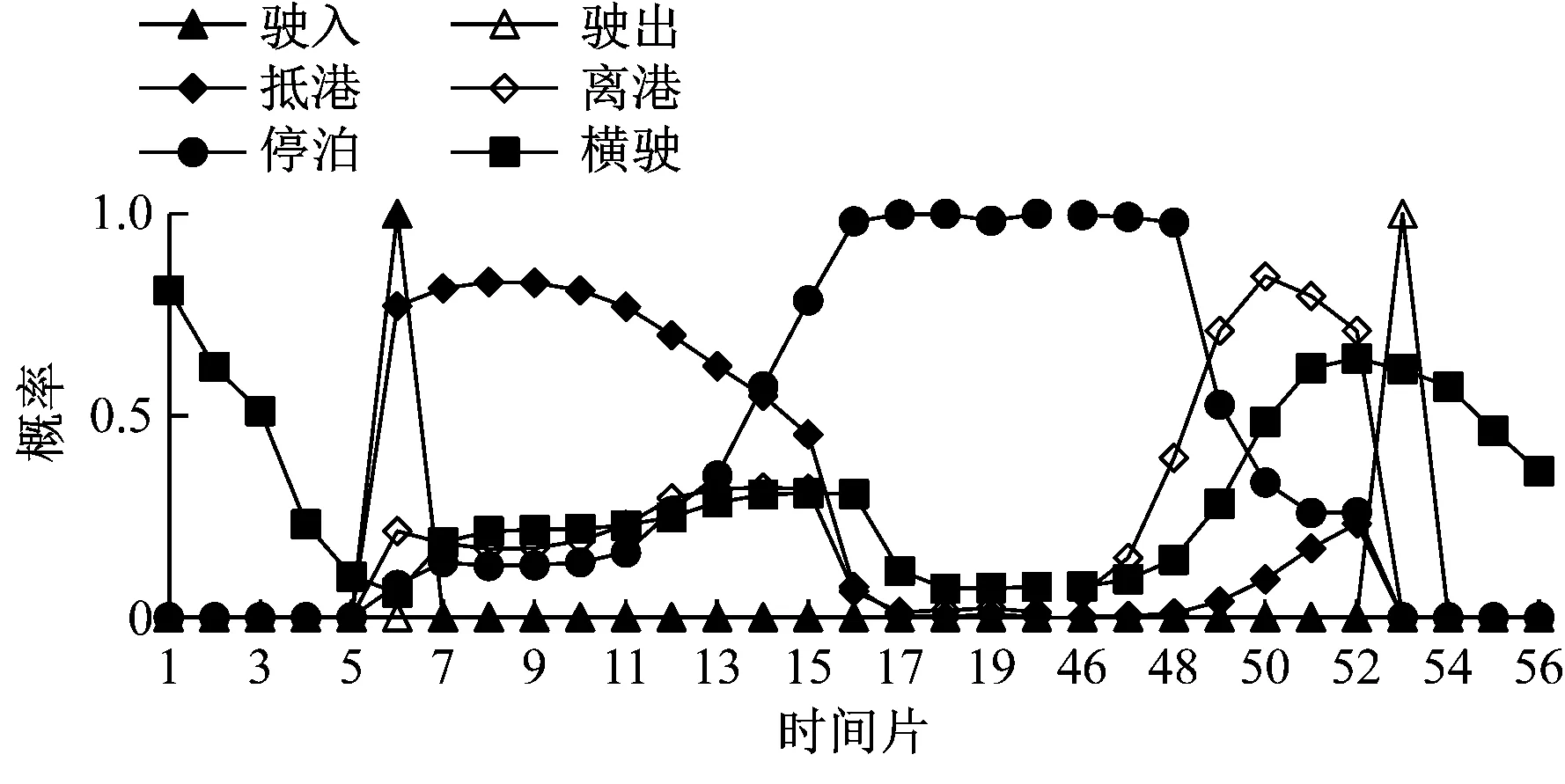
b) 部分行为推理结果

c) 转向行为推理结果

d) 变速行为推理结果

1) JiangCheng4Hao (ferry) hasEvent Arrival in WuHanGuan (dock) BeginTime at 2014/1/1T07:01:35+8:00。

2) JiangCheng4Hao (ferry) hasBehavior Berth in WuHanGuan (dock) BeginTime at 2014/1/1T07:03:46+8:00。

3) JiangCheng4Hao (ferry) will hasEvent AcrossRiver in WuHanGuan (dock) at 2014/1/1T07:12:06+8:00。

5 结束语

面向智能航海应用，利用语义模型与动态贝叶斯网络建立一种船舶行为动态推理机制，典型的船舶靠离泊模型证明所提出的方法能准确地识别并预测动态船舶行为。推理结果可提供给船舶交通服务(Vessel Traffic Service, VTS)操作员、引航员、船员及智能船舶等明确、精准的动态船舶行为信息；具有标准化结构的语义信息便于应用到智能船舶系统中，可使智能船舶动态感知并预测周围船舶的行为，及时规避风险，避免紧迫局面；推理结果可表达为高层次语义信息，压缩大量信息价值低的数据，易于存储、查询和共享。

本文没有考虑水文气象等自然环境对船舶行为的影响，以后将研究气象水文影响下的船舶行为语义模型。外界环境不一定是稳态的，船舶行为的网络结构也可能随时间变化而变化，因此需要建立变结构、变参数的船舶行为模型。