连续施工水域船舶航线规划
刘 毅, 谢新连, 何 傲, 辛剑英
(1.大连海事大学 综合运输研究所, 辽宁 大连 116026;2.东南大学 交通学院,南京 211189)
所谓连续施工水域,是指假设在施工水域中的施工点分布比较密集,且在距离施工点附近一定范围内的水域将会受到施工作业的影响。各个施工点的影响范围相互交织,形成一个带状或网状的连续施工影响区域。海上施工水域是海上交通事故的高发区域,由于在施工水域中环境复杂多变,船舶在施工水域的航线规划难度也极大。特殊水域中的船舶航线规划的发展进程将在很大程度上决定现代无人驾驶技术的发展水平。早在现代智能无人船出现之前,路径规划就已在工业机械手领域中得到广泛的应用,并且有大量的研究。[1-7]传统的船舶航线规划是指在静态和动态障碍物并存的环境中,寻找一条从已知起点到终点的满足一定评价标准的航行路径,使得船舶在航行过程中能够安全可靠地避开所有的障碍物。[3]常见的路径规划方法有动态规划法、最速下降法、最优控制法、启发式搜索法、神经网络法、模拟退火法和遗传算法等。由于每种路径规划算法都存在一些缺陷,所以,实际应用的方法大多数是基本路径规划算法的改进算法,或者融合数种基本路径规划算法的算法。[8]
目前,既有对飞行器航行路径规划的研究,也有对无人船和机器人的路径规划方面的研究,他们研究的问题主要集中在普通或正常环境下各种交通工具的路径的规划。然而在特殊环境下的路径规划研究则较为罕见。而且,船舶的路径规划和航线设计有其自身的特殊性,船舶在水中的操纵性能和陆上的交通工具或机器人也有较大差异,因此不能直接使用其他交通工具的路径规划方法。船舶在海上航行时事故频发的主要区域就是海上的施工区域,海上施工种类繁多,对其附近船舶的影响各不相同,为保障船舶能够顺利通过施工水域,有必要对施工水域的船舶航线规划进行相关的研究。
1 连续施工水域航线规划问题描述
船舶在海上和江上航行有时会经过一些施工水域,并且在有的水域中同时包含多个水面和水下施工地点,当在同一片施工水域中包含多个施工点时,船舶在航行时就会变得复杂和危险。例如,当建设跨海大桥时,会在海面形成一个链条状的施工影响区域见图1。如果没有绕开施工水域的捷径,船舶只能够经过施工水域。

图1 连续施工水域环境示意
在连续施工水域环境中如图1所示,用五角星点pi代表施工水域中分布着的施工点,用施工点附近的虚线圆圈Si代表施工点的影响的区域范围,各施工点产生的施工影响区域相互交织,连接形成一个长长的带状影响区域,如何在此施工水域中寻找出一条满足安全性和经济性要求的航线,以保证船舶顺利通过施工水域,是一个需要解决的实际问题。
2 连续施工水域航线规划数学模型
一般的施工水域的航线规划是给船舶设计出一条能够避开所有施工危险区域的最短航线。因此,在这种情况下只需要建立单目标的数学模型,其优化目标只有一个,即是航线的总距离最短。当施工水域是比较密集的连续带条形时,施工水域航线规划的数学模型将会是一个多目标规划的数学模型,一个目标是使规划的路径航线最短,另一个目标是航行风险值最小。这两个目标在连续施工水域的航线规划中是相互对立的,两个目标是不能同时得到满足的,因为航线最短的路径会穿过施工水域,而风险最小的安全航线是绕过施工水域,但绕过施工水域在实际情况中是无法实现的。因此,对连续施工水域中的船舶航线规划需要建立特殊的数学模型来达到航线规划的目的。
在进行以上分析以后,为在连续施工水域中寻找出一条满足航行安全要求的可行航线。为此,建立航线规划数学模型。
(1)
(2)
s.t.∀θPj∈(1,…,k)≤φmax
(3)
RPj∈(1,…,k)≥λL
(4)
D≥Dmin
(5)
模型解释:式(1)为模型的第1个目标方程,表示规划的航线尽可能短。式(2)为模型的第2个目标方程,表示求整条航线的危险度尽可能小,等价于航线安全度尽可能高。L为在施工水域中由起点S到终点T的一条曲线,即施工水域中的一条航线,可以把L分解成n个小段,第i个小段可由微分单元ds表示,假设在施工水域中任意位置(x,y)处的危险度服从函数关系z(x,y),则沿着规划好的航线进行曲线积分,就可得到整条航线的危险度值。式(3)为船舶在pj节点处的转向角必须小于航线设计航速下船舶的最大安全转向角φmax,在一般情况下φmax≤90°。式(4)为在pj节点处船舶进行转向时,航道必须满足船舶最小转弯半径的要求,其中:L为船舶的长度,m;λ为航道在不同设计航速下所取的最小转弯半径与船长的比值。式(5)为规划航线与危险区域的最小距离的约束,其中:D为航线某处与危险区域的最小距离,m;Dmin为船舶与危险区域的最小安全距离,m。
3 连续施工水域中的风险模型
上述主要对连续施工水域的船舶航线规划建立数学模型,在数学模型中涉及施工水域的风险模型,以下主要介绍如何为各个施工点建立一个合适的风险模型,这也是解决连续施工水域船舶航线规划的关键。在连续施工水域中距离施工点附近的一定范围内的水域将会受到施工作业的影响,而且距离施工点距离越近,施工作业对船舶航行的影响越大,发生各种海上交通事故的概率也就越大。
因此,假设在施工水域中存在一个施工点qi(xi,yi),在其附近存在任意一点pj(x,y)。在pj处受到施工点qi施工作业的影响的函数由zi(x,y)来表示,使用旋转椭球体模型来表示施工水域中施工点对周围产生的影响,则zi(x,y)的表达式为
(6)
式(6)中:ci值代表qi处的施工点的施工作业所产生影响的最大辐射范围,当任意点pj(x,y)的所在位置与施工点qi的欧氏距离>ci时,施工作业对点pj不再产生任何影响。当施工水域中的点pj与施工点qi的位置相同时zi(x,y)取得极大值为1时,其物理意义表示当前规划的船舶航线正好穿过施工点,因此发生交通事故的概率为1。
由于在施工水域中分布着若干个施工点,因此,施工水域中的任意一点pj处的风险度值为施工水域中所有施工点对其产生的施工影响的总和,用Zj(x,y)来表示在施工水域中的任意一点pj所受到的所有施工点对其产生影响的总和,则Zj(x,y)的表达式为
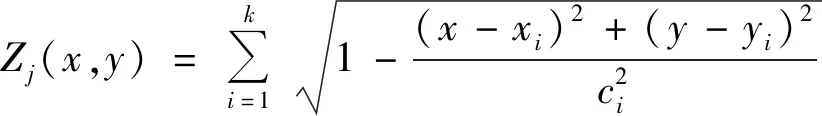
(7)
式(7)中:k为施工水域中分布着的施工点的个数。现在称函数Zj(x,y)为连续施工水域中任一点pj处的船舶航线规划的风险模型。船舶经过连续施工水域时承受的风险见图2。

图2 风险模型示意
施工水域分布着10个海上施工作业点如图2所示,每个施工作业点的影响范围都是半径为c的圆型区域,各个区域之间相互交织形成一条连续的施工作业影响带。在施工作业影响带中,各个施工点处为施工影响带上的风险极大值点。
4 连续施工水域中的船舶航线规划的求解
在完成连续施工水域的航线规划的风险模型构造的基础上,需要在施工水域中寻找出一条既满足船舶航行安全要求,又满足航线总距离尽可能短的最优航线作为船舶通过施工水域的航线。为给在连续施工水域环境下的船舶规划航线,首先需要在施工水域中建立航线网络,然后再在航线网络中寻找到一条最优航线解。
在构建连续施工水域的船舶航线网络时,先考虑连续施工水域航线规划数学模型的约束条件式(6),即在施工点附近半径为Dmin的水域为不可航行区,本文Dmin的值取10,施工点的影响范围c取20。根据模型构造出的连续施工水域环境下的船舶航线规划路网见图3。

图3 连续施工水域路网示意


最后再综合评价各条航线。为更好地体现多目标优化模型中各个目标方程的作用,设计航线综合评价模型的表达式为
minZ=Z1×(1+λ×Z2)
(8)
式(8)中:λ为修正系数,调整λ的值以符合各种施工水域不同的实际情况,以得到更加合理的规划结果,本文中λ取值为0.05。由综合评价模型计算得到的各条航线的最终评价结果见表2。

表1 各条航线的路径长度和风险度值

表2 各条航线的最终评价结果
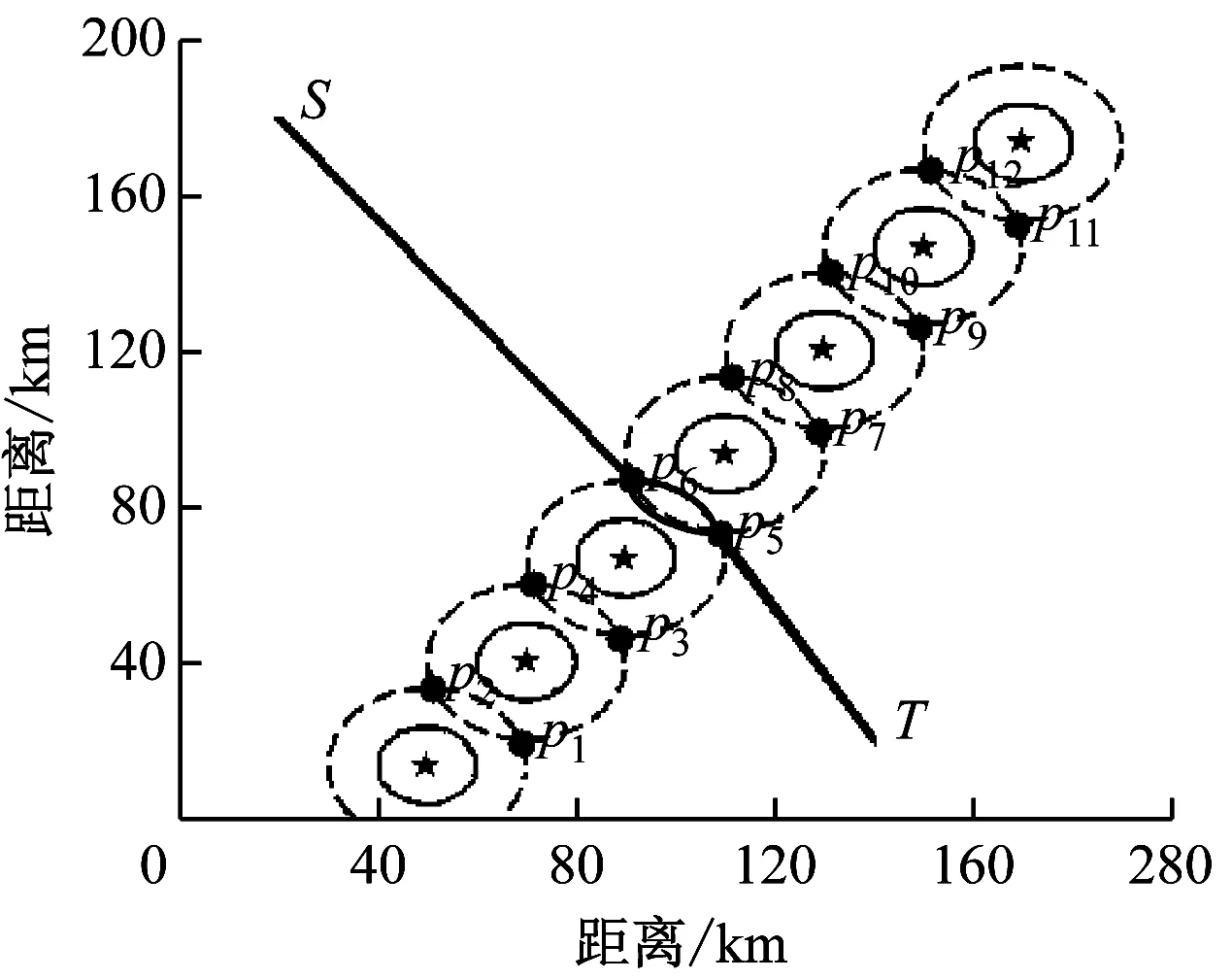
图4 连续施工水域结果示意
如图4中所示的航线包含两条路径,其路径总距离和风险值都相同,船舶驾驶员可根据自己的驾驶习惯选择其中一条航线作为船舶通过连续施工水域的航线。
5 结束语
主要研究船舶穿行连续施工水域的航线规划问题,为解决船舶在连续施工水域中的航线规划问题建立一个非线性多目标的数学模型。另一方面为量化船舶在施工水域中受到各个施工点的影响,建立船舶在施工水域的风险解析模型。在求解建立的航线规划的数学模型时,首先在施工水域中构造满足航行安全基本要求的航线网络,然后分别计算各条航线的航线总长度和航线的通航风险度值,最后通过建立的航线评价数学模型最终得到通过连续施工水域的最优航线。

