九轴陀螺仪在AGV自主导航中的应用设计

(青岛科技大学 信息与科学技术学院，山东 青岛 266061)

0 引言

自动引导车辆AGV(automated guided vehicles)是指装备有电磁或光学等自动引导装置，能够沿规定的导引路径行驶，具有安全保护以及各种移栽功能的运输车[1]。

目前比较常见的AGV导航方式有激光导航、电磁导航、坐标导航和光学导航等。从使用效果来看，激光导航和光学导航对环境要求过高；电磁导航需要对路面安装金属线，并且导航路面难以更改或者扩展；坐标导航则路面安装定位块较复杂，工作量大而且定位不准确。本文以九轴陀螺仪进行导航，对周围环境要求较低，导航路径灵活，而且导航精度较高，后期维护成本也较低，是一种较为理想的导航方式[2]。

本课题为九轴陀螺仪在AGV自主导航中的应用设计，是一种全方位移动平台控制系统，通过对单台或两平台同步移动柔性连接、通过无线控制使2台AGV移动平台协同运动，使其灵活应用在空间有限、机动性要求高的场合。在每台AGV小车上面安装MPU9250九轴陀螺仪(3轴加速度计、3轴陀螺仪、3轴磁力计)，系统采集九轴陀螺仪数据，通过卡尔曼滤波进行数据融合输出融合后的航向角，然后AGV行驶过程中应用该导航角通过PID控制算法进行控制实际行驶方向，从而引导小车朝着目的地方向行驶[3]。

1 应用场景

本设计为在动车车体装配车间使用，系统使用两个AGV小车共同完成动车车体在车间的移动。AGV小车使用麦克纳姆轮，正常工作时，从车接受主车发出的指令，两者协调同步运行。两个AGV小车导航行走的现场平面如图1所示(默认为30m×15m)，AGV导航车的平时停车位置点与目标位置点如图1已标出。

图1中以UL为停车点，TB为目标点为例进行研究。首先需要确定AGV从UL到TB初始航向角，即X、Y轴的偏角或者地理坐标的夹角。然后通过卡尔曼滤波对航向角进行融合，行驶过程中再通过PID算法不断控制运动角度，直到最终到达TB。其他停车位置到目的位置的研究过程类似。应用场地的坐标始终以UL为坐标原点，向东为X轴，向北为Y轴，分别以UL、UM、UR、DL、DM、DR为出发原点，以TA、TB为目标点，计算各种出发点、目标点组合，出发时的初始航向角。本设计默认X=30 m，X1=15 m，X2=7 m，Y1=7.5 m，Y=23 m。

图1 AGV导航控制示意图

AGV小车装有麦克纳姆轮，即每个轮子在没有任何转角的情况下，通过控制每一个轮子的速度和方向实现3自由度的全方位移动。AGV小车车顶安装反射板，停车板上方安装激光扫描仪，激光扫描仪通过对反射板的扫描判断小车是否到达停车板附近。目标位置点TA和TB处有停车板，停车板设计为长方形，中轴线平行于TA和TB连线，正好容小车停下。AGV小车配有遥控器，当小车到达停车板附近时小车会发出警报，此时需要小车的操作人员通过遥控器指挥小车停到停车板上面。

2 坐标系与姿态角

本课题用到车体坐标系、场地坐标系和地理坐标系。因车体坐标系是随时变动的，故需要依靠不变的地理坐标系确定航向角，因此需要将车体坐标系转换到地理坐标系，再进行相关角度计算[4]。

2.1 车体坐标系

如图2所示。取平面图中小车的实际停放位置中心为坐标原点O，OXb轴的正向指向AGV小车的前方，OYb轴的正向指向AGV小车的右侧，OZb轴的正向指向天，建立车体坐标系。

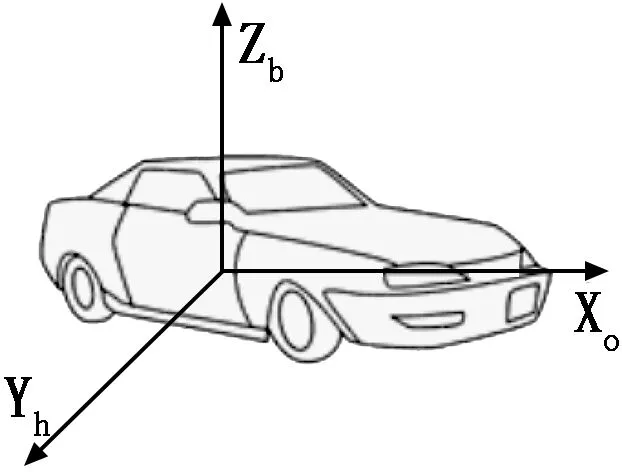
图2 车体坐标系图

2.2 地理坐标系

如图3所示。取小车的实际停放位置为坐标原点O，OXn轴的正向指地球的东方，OYn轴的正向指向地球的北方，OZn轴的正向指向天，建立地理坐标系。

图3 地理坐标系图

2.3 场地坐标系

以场地的右方作为X轴，下方为Y轴进行定义，用于计算场地的导航角。场地坐标系与地理坐标系之间的夹角为α。

2.4 坐标变换矩阵

本课题是将车体坐标系OXbYbZb变换到地理坐标系OXnYnZn[5]，再对九轴数据进行卡尔曼滤波处理，最后得到融合后的航向角。

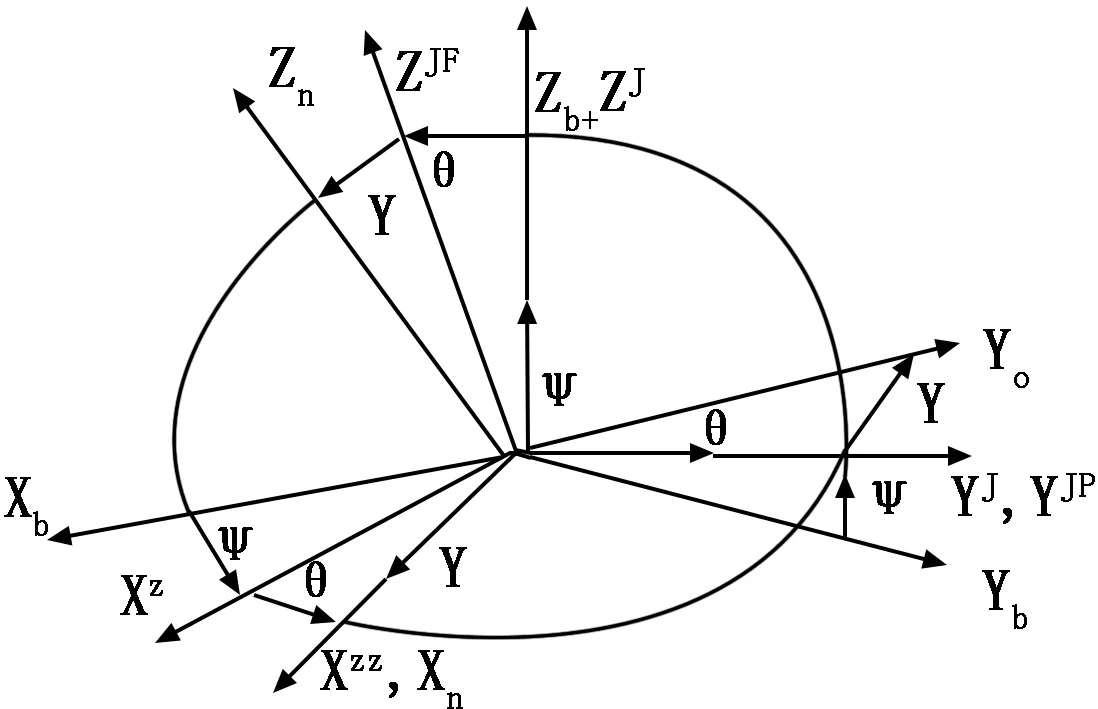
图4 车体坐标系与地理坐标系变换图

如图4所示，车体坐标系分别绕Z轴旋转Ψ度、绕Y轴旋转θ度、绕X轴旋转γ度，最后与地理坐标系重合。公式1即车体坐标系到地理坐标系的坐标变换矩阵，如下所示：

C=C1·C2·C3=

(1)

3 卡尔曼滤波与数据融合

本文首先用卡尔曼滤波对磁力计和加速度计的测量角度进行滤波，然后对磁力计和加速度计的输出角度进行融合得到融合后的航向角[7-9]。

3.1 卡尔曼滤波模型建立

本文认为磁力计、加速度计的角度变化都符合线性关系，故在卡尔曼滤波中建立状态方程和量测方程。

(2)

(3)

将AGV状态方程转换为加速度计相关量的方程，如公式4所示。将AGV的测量方程转换为磁力计相关量的方程，如公式5所示。

(4)

(5)

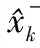
3.2 数据融合

卡尔曼滤波是用递推的形式，对未来某一时刻状态进行估计。本文以加速度计的航向角作为测量值，加速度计的航向角作为预测值，然后根据前一时刻的预测值和测量值来估计当前时刻系统的最优值。

本文首先通过计算得到加速度计的航向角，然后通过卡尔曼滤波模型公式计算航向角的测量值和下一时刻的预测值，把磁力计测量的角度数据和加速度计计算的角度数据作为卡尔曼滤波的输入，通过卡尔曼滤波5个公式计算得到融合后的航向角。

首先根据系统上一次得来的最优值计算出当前的估计值和协方差。

γk=Aγk-1+Bφk-1

(6)

(7)

再根据协方差大小计算出卡尔曼增益的大小。

(8)

最后根据当前估计值和测量值计算出当前最优值和误差协方差。

ω=γk+Kk(yk-Hγk)

(9)

(10)

4 PID控制算法

由于AGV使用采样式控制，不能连续不断的输出信号，故不能连续控制，所以本课题使用数字PID控制算法，即在模拟PID算法基础上，将微分和积分项进行离散化处理。

4.1 PID控制算法

PID控制器为一阶控制器，设定值与输出值之间的差值组成系统偏差，将系统偏差与比例系数P、积分系数I和微分系数D通过一阶线性关系构成控制量，控制被控对象[10]。将输入角度与输出行驶角度做差得到e(k)作为PID的输入，小车的输出为实际运行角度θ(k)。

图5 PID控制原理图

在实际应用中，需要通过大量实验来确定PID三个参数[12]。其控制规律为：

(11)

其中:θ(k)是k时刻的航向角；Kp为比例系数；TI为积分常数；TD为微分常数；θ0为初始角度。

4.2 数字PID控制算法

数字PID算法有两种离散化的方法，分别是位置式和增量式，由于增量式的计算较简单，故本课题选用增量式PID算法[11-12]。也就是把采样周期设为T，采样序号设为k，那么离散化的kT就可以近似替代连续采样T。用和的形式替代积分形式，用增量式替代微分式，就可以获得离散化的数字PID公式(12)和公式(13)。

(12)

Δθk=θk-θk-1=

Aek+Bek-1+Cek-2

(13)

其中：θk代表计算机第k次采样时的输出；ek代表第k次采样时输入数据的偏差值；KI代表积分系统，KI=KpT/TI；KD代表微分系数，KD=KPTD/T。

卡尔曼滤波输出的融合后的航向角作为数字PID算法中的输入值，每隔一个时间周期都要重新计算从小车当前位置到目标位置的航向角，作为小车下一次行驶的输入航向角，此输入航向角与融合以后的航向角进行对比，从而进行PID调节。

5 实际应用

5.1 系统编程流程

AGV导航前期，首先使用九轴陀螺仪的磁力计测量出工作场地与地理坐标系的夹角α，车体停放的位置姿态与工作场地平行；根据图1所示的几何尺寸，使用场地坐标计算出发地点到目标地点的夹角β，并与α结合形成初始的车体导航角；在出发地点，通过麦克纳姆轮转动小车的车头，使车头朝向目标点。

启动AGV车体向目标点出发。在行驶过程中，通过九轴陀螺仪的磁力计读取γ角数据，通过九轴陀螺仪的加速度计计算在采样周期内车体移动的夹角φ，其计算如公式14所示。

(14)

其中：k-1时刻的坐标是(X1,Y1),k时刻的坐标值为(X2,Y2)。

将它们作为卡尔曼滤波的输入，通过卡尔曼滤波进行数据融合输出融合后的航向角，AGV按照融合后的航向角控制行驶，同时通过PID算法调整AGV的行驶方向，使其更准确的朝着目标点行驶。

当小车到达停车板附近时，AGV小车会发出警报，此时需要小车操作人员用遥控器手动控制小车移动到停车板上。此时小车需要按照初始出发时的角度调整落位。

全方位移动平台可以通过遥控器选择单车或者两车系统。在理想状态下，当两移动平台协同运动时，从车受控地与主车保持相同的姿态。

5.2 场地航向角计算

实际应用中，只考虑X轴和Y轴，不考虑Z轴。场地如图1所示，当停车点和目的地距离默认时，如果AGV小车从停车点UL(0,0)到目标点TB(23,7.5)移动，那么需要先把车体坐标与场地坐标结合转换到地理坐标系中，场地坐标的出发航向角为18.06°。小车出发后通过卡尔曼滤波把九轴陀螺仪磁力计测量的角度数据和根据加速度计计算的角度数据滤波融合后的输出控制航向角，然后通过PID积分控制算法不断地修正AGV小车运动过程中的运行角度，直到到达TB为止。其他停车点到目标点的移动过程类似。

AGV小车的导航图如图1所示，以UL为原点建立坐标系，使车体坐标系与地理坐标系原点重合。AGV小车从各出发点到目标点的初始航向角的关系如表1所示。

5.3 系统应用步骤

当AGV小车行驶的场地如图1所示，而且停车点与目标点的距离是默认距离时，将小车从停车点UL(0，0)通过自主导航的形式到达目标点TB(23,7.5)，行驶过程如下：

1)AGV小车出发之前，将车体坐标系转换到地理坐标系使两者重合，计算出小车从出发点到目标点的角度，本课题中的该角度为18.06°，计算场地坐标系与地理坐标系之间的夹角，本课题中假设场地坐标系与地理坐标系完全重合，即夹角为0°。将二者进行相加，得到的角度为小车的初始航向角。

2)通过麦克纳姆轮原地调转AGV小车的车头，转动角度为初始航向角，本课题中为18.06°。

3)小车出发后，通过四元数法进行三轴陀螺仪和三轴磁力计角度的融合(此时没有去除噪声)。

4)将三轴磁力计和三轴陀螺仪融合后的角度与三轴加速度计的航向角作为卡尔曼滤波的输入值，对角度进行卡尔曼滤波处理，将系统中与信号无关的噪声干扰去除，然后将两个角度进行融合，得到融合后的航向角。首先进行时间的更新，确定先验估计值和误差协方差预估计矩阵，然后再进行测量更新，最后确定小车的卡尔曼滤波增益、最优估计和误差协方差矩阵，时间更新与测量更新交替进行，直到小车到达目标点为止。

5)小车行驶过程中，实时的计算小车的当前位置与目标位置的航向角，通过数字PID控制算法进行控制，使小车更准确的进行自主导航。

6)当小车行驶至目标点附近时，目标点附近的激光扫描仪会发出警报声，此时需要操作人员使用遥控器控制小车准确的停到目标点的停车板上面。

5.4 系统仿真

用Matlab将AGV从停车点UL到目标点TB点进行仿真，其中停车点与目标点的长度使用默认距离的十倍，真实轨迹代表从停车点到目标点直线行驶，路径使用黑色标记；观测轨迹为小车没有进行卡尔曼滤波之前的行驶轨迹，路径用蓝色标记；滤波轨迹为小车进行卡尔曼滤波之后的行驶轨迹，路径用红色标记。从图6中可以看出AGV小车的理想轨迹是从停车点到目标点直线行驶，但是实际行驶过程中小车并不能如此理想的从停车点到达目标点，从图中可以看出小车在没有滤波的情况下行驶过程毫无章法可言，忽上忽下而且偏离理想轨道的距离较远，最高达到40米，行驶路径过长而且复杂，而通过卡尔曼滤波之后的小车行驶过程中都是紧紧围绕理想轨迹周围运动，偏离理想轨迹的距离基本控制在10米以内，由此可以看出AGV通过卡尔曼滤波之后小车运行轨迹的精确度有了明显的提高，行驶距离更短，导航过程更加精确，由此可以证明卡尔曼滤波在AGV小车的自主导航过程中是起到一定作用的。

AGV小车在图7的行驶过程中，对其误差进行仿真，图中理想轨迹与普通轨迹之间的误差叫做滤波前误差，用绿色点表示，而滤波后误差指滤波轨迹与理想轨迹之间的误差，用红色点表示，从图中可以看出，滤波前小车从停车点到目标点行驶过程中的误差较大，而且误差大小很不稳定，波动幅度达到30左右，而滤波后的误差相对滤波前而言比较平稳，除了小车刚启动时误差较大，波动幅度达到13左右，后续行驶过程中误差相比较稳定，波动幅度控制在5以下，由图中两个颜色的折线图可以看出滤波前后小车行驶过程中的误差有了明显的提升，小车行驶过程更加稳定，导航过程更加精准，更加验证了卡尔曼滤波对小车自主导航过程中起到了重要的作用。

表1 单变量下AGV小车的航向角

图6 系统仿真图

图7 系统误差图

6 结论

AGV小车运行过程中，使用卡尔曼滤波和数字PID控制算法，使小车行驶过程更精准，停车点使用与人工控制相结合的方式，可以使小车停车更精确。本课题对AGV小车在不定长导航图的初始导航角度进行研究，可以根据研究结果，确定所有类似导航场景中的初始航向角。该设计通过编程实现，很好地完成了系统的导航功能，数据融合效果良好。