Parseval K-框架的一些等式与不等式

傅元康, 朱玉灿

(福州大学数学与计算机科学学院, 福建 福州 350108)

0 引言

Hilbert空间中的框架的概念, 最早是在1952年文献[1]中研究非调和Fourier级数时引入的. Hilbert空间中的框架作为标准正交基的一种推广, 在很多领域中发挥着重要作用, 比如: 压缩感知[2]、 信号采样[3]等. 更多关于Hilbert空间中的框架介绍可参见文献[4].

2012年, 文献[5]在研究关于有界线性算子K的原子系统时引入了K-框架的概念. 随后，文献[6]引入了ParsevalK-框架的概念. 当前, 诸多学者已经得到了一些关于K-框架的研究结果, 详见文献[6-10].

2006年, 文献[11]证明了在不需要噪声相位或其估计的情况下也可实现对信号的重构. 而在计算重构的有效算法时, 文献[12]提出了一个Parseval框架的等式与不等式. 在随后的几年中, 该结果被相关学者进行了推广[8, 13]. 本研究把该结果推广到ParsevalK-框架上, 并对ParsevalK-框架的上指标和下指标的性质进行讨论.

1 预备知识

定义1[4]设序列{fi}i∈N⊂H, 若存在正数A和B满足

则称序列{fi}i∈N为H的框架, 其中A和B分别称为框架的下界和上界. 如果上述不等式的右边成立, 则称序列{fi}i∈N为H的Bessel序列, 并且可定义有界线性算子T如下：

称T为Bessel序列{fi}i∈N的合成算子.T的共轭算子T*为

T*:H→l2,T*f={〈f,fi〉}i∈N(f∈H)

称T*为Bessel序列{fi}i∈N的分析算子. 令S=TT*, 则

称S为Bessel序列{fi}i∈N的框架算子.

定义2[5]设K∈B(H), 序列{fi}i∈N⊂H, 若存在正数A和B满足

则称序列{fi}i∈N为H的K-框架, 其中A和B分别称为K-框架的下界和上界. 当K=I时,K-框架就是框架.

定义3[6]设K∈B(H), 序列{fi}i∈N⊂H, 若存在正数A满足

则称序列{fi}i∈N为H的紧K-框架. 特别地, 如果A=1, 则称序列{fi}i∈N为H的ParsevalK-框架.

定义4设K∈B(H)且K≠0, 若序列{fi}i∈N⊂H满足

则称序列{fi}i∈N为H的K-标准正交基.

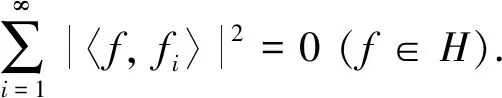
定义5[7]设K∈B(H), 序列{fi}i∈N为H的K-框架, 若存在H的Bessel序列{gi}i∈N满足

则称序列{gi}i∈N为{fi}i∈N的K-对偶Bessel序列.

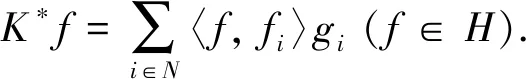
定义6[7]设K∈B(H), 若序列{fi}i∈N为H的K-框架, 则{fi}i∈N的自然K-对偶Bessel序列是其所有K-对偶Bessel序列中分析算子的范数最小的K-对偶Bessel序列.

引理1[4]若T∈B(H)且具有闭值域, 则

1) 存在唯一的T+∈B(H)满足

N(T+)=R(T)⊥，R(T+)=N⊥(T),TT+f=f(f∈R(T))

称T+为T的伪逆算子. 特别地, 如果T为可逆的有界线性算子, 则T+=T-1.

2)T+T为H上的正交投影算子,T+T(H)=N⊥(T).

引理2[14]若T∈B(H), 则

引理3[15]设A,B∈B(H), 则下列命题等价：

I)R(A)⊂R(B).

II) ∃λ≥0, 使得AA*≤λ2BB*.

III) ∃C∈B(H), 使得A=BC.

引理4若序列{fi}i∈N和{gi}i∈N为H的两个Bessel序列, 则对于任意J⊂N和任意f∈H, 有

证明 对于任意J⊂N和任意f∈H, 有

引理5设K∈B(H), 序列{fi}i∈N为H的ParsevalK-框架, 若K具有闭值域, 则

KK+fi=fi(i∈N)

证明 由于{fi}i∈N为H的ParsevalK-框架, 故不妨设{fi}i∈N的合成算子为T. 由定义3和引理3, 易知R(K)=R(T). 又由T的定义, 知fi∈R(T)(i∈N). 故由引理1的1), 有引理5成立.

引理6设K∈B(H), 序列{fi}i∈N为H的K-标准正交基, 若K具有闭值域, 则

①K+=K*.

② 〈K+fi,K+fj〉=δij(i,j∈N).

证明 ①由引理1的1)于K具有闭值域, 知K*具有闭值域. 故由引理2, 有N(K*)=R(K)⊥,R(K*)=N⊥(K). 根据引理1的1), 知若要证明K+=K*, 只需证明K=KK*K即可. 由于{K+fi}i∈N为{fi}i∈N的自然K-对偶Bessel序列(见文献[16]中的定理2.10), 则根据定义5可知对于∀f∈H, 有

对于∀j∈N， 取f=K*fj, 那么根据定义4和引理5可得

最后结合上述两个等式, 即可知对于∀f∈H, 有

② 由于K+=K*, 故根据定义 4和引理5, 知对于∀i,j∈N, 有

〈K+fi,K+fj〉=〈K*fi,K+fj〉=〈fi,KK+fj〉=〈fi,fj〉=δij

2 主要内容与结论

定理1设K∈B(H), 序列{fi}i∈N为H的ParsevalK-框架, 若K具有闭值域, 则对于任意J⊂N和任意f∈H, 有

证明 根据引理5, 知对于∀i∈N, ∀f∈H, 有

由于{K+fi}i∈N为{fi}i∈N的自然K-对偶Bessel序列(见文献[16]中的定理2.10), 故根据文献[8]的定理2.5, 分别令文献[8]的定理2.5中的{gj}j∈J和{fj}j∈J为： {fi}i∈N和{K+fi}i∈N, 即可得定理1.

注3当K=I时, 通过定理1, 可得到文献[12]中的定理3.2和命题4.1.

定义7设K∈B(H)且K≠0, 序列F={fi}i∈N为H的ParsevalK-框架, 若K具有闭值域, 则对于任意J⊂N和任意f∉N(K*), 令

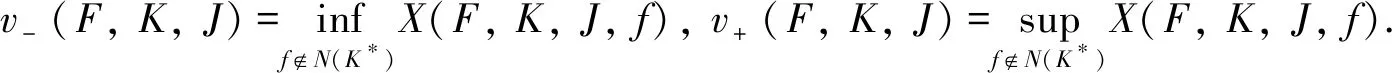
定理2设K∈B(H)且K≠0, 序列F={fi}i∈N为H的ParsevalK-框架, 若K具有闭值域, 则v-(F,K,J),v+(F,K,J)具有如下性质：

2)v-(F,K,J)=v-(F,K,Jc),v+(F,K,J)=v+(F,K,Jc).

3)v-(F,K, ∅)=v+(F,K, ∅)=1,v-(F,K,N)=v+(F,K,N)=1.

4) 若序列F={fi}i∈N为H的K-标准正交基, 则对于任意J⊂N, 有

v-(F,K,J)=v+(F,K,J)=1.

即v+(F,K,J)≤1.

2) 根据定理1易到.

3) 根据定义3和注2易得.

4) 由引理6, 知〈K+fi,K+fj〉=δij(i,j∈N). 故根据定义4, 知对于任意J⊂N和任意f∉N(K*), 有

故有v-(F,K,J)=v+(F,K,J)=1.

注4当K=I时, 通过定理2, 可得到文献[13]中的定理2.3.