一个构造等能量图族的方法

王洪波, 林 泓

(集美大学理学院， 福建 厦门 361021)

0 引言

设G=(V,E) 是顶点集为V={v1,v2, …,vn}而边集为E的简单图.G的邻接矩阵定义为A(G)=(aij)n×n， 其中aij=1， 若vi与vj相邻； 否则aij=0. 由于A(G)是实对称的， 故其特征值是实数[1]. 设λi1,λi2, …,λil是A(G)的全部互异特征值， 它们的代数重数分别为m1,m2, …,ml， 这里m1+m2+…+ml=n. 则A(G)的所有互异特征值连同它们的重数被称为G的谱.

定义G的能量为图的邻接矩阵的特征值的绝对值之和. 图的能量作为一类在化学中有重要应用的图指标， 已被许多学者所研究[2-3].

具有相同的谱的两个非同构图称为同谱图. 若两个非同构图有相同的能量， 则称它们为等能量的. 在许多的文献中都有等能量图的例子[4-7]， 本文将介绍一种构造等能量图的方法. 先给出若干正则图的联并图的谱， 它的谱是由正则图的谱(去掉每个正则图的第一个最大特征值)和一个由图G决定的辅助矩阵的特征值组成. 接着利用这个刻划给出了一个利用正则图的联并图构造等能量图的方法. 作为应用， 最后给出了一些等能量图的例子.

1 联并图

设G和H是两个图，G和H的并图G∪H定义为：V(G∪H)=V(G)∪V(H)，E(G∪H)=E(G)

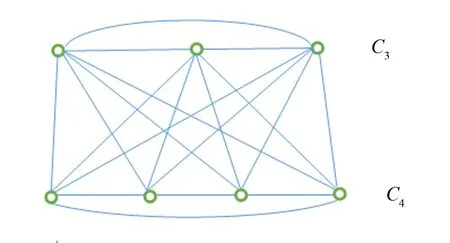
图1 联并图K2[C3, C4]Fig.1 Joined union graph K2[C3, C4]

∪E(H). 设G是顶点数为n的简单图，Gi=(Vi,Ei)，i=1, 2, …,n是任意n个简单图.G1,G2, …,Gn的联并图G[G1,G2, …,Gn]=(W,F) 定义为：

显然联并图G[G1,G2, …,Gn] 就是在G1,G2, …,Gn的并图上再添加一些新边： 若G中的顶点vi与vj相邻， 则将Gi的所有顶点与Gj的所有顶点相连.

例如， 在C3∪C4中将C3的所有顶点和C4的所有顶点相连就得到K2[C3,C4]， 如图1所示.

2 联并图的谱

定理1设G=(V,E) 是顶点数为n的简单图， 其邻接矩阵为A(G)=(aij)n×n， 而Gi=(Vi,Ei) (i=1, 2, …,n) 是顶点数为mi的ri-正则图， 其邻接矩阵的特征值为ri=λi1≥λi2≥…≥λimi. 则λij(i=1, 2, …,n;j=2, 3, …,mi) 及矩阵A*的特征值就是联并图G[G1,G2, …,Gn] 的全部特征值， 这里

证明 记H=G[G1,G2, …,Gn]. 则H的邻接矩阵具有如下的形式：

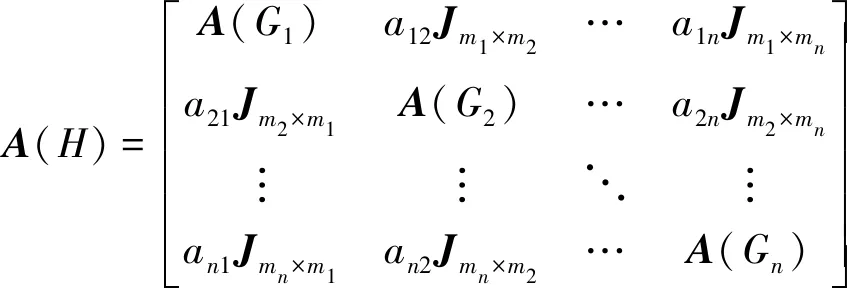
其中:A(Gi) 是Gi的邻接矩阵；Jmi×mj是mi×mj全1矩阵，i,j=1, 2, …,n.

对任意给定的i∈{1, 2, …,n}， 设ui1(mi维全1向量， 记为1mi),ui2, …,uimi为A(Gi) 的对应于λi1,λi2, …,λimi的mi个互相正交的特征向量.

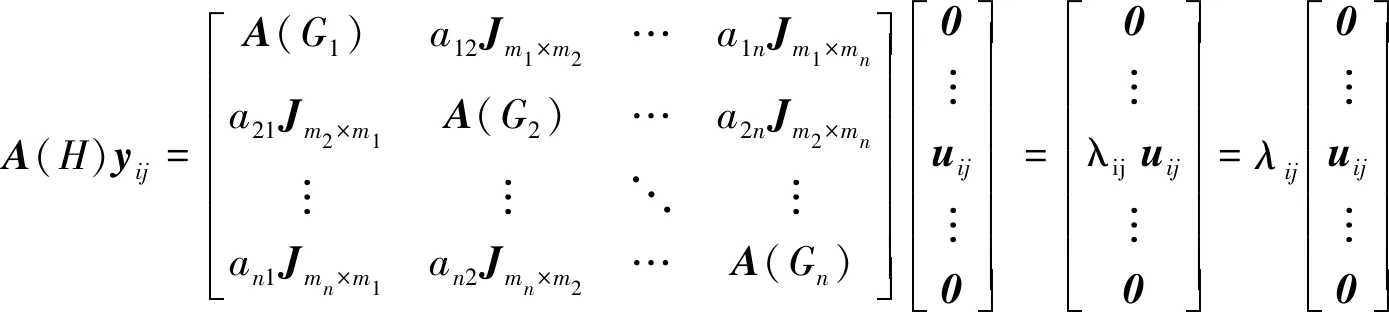
由此可知，z1,z2, …,zn满足方程组

因为z1,z2, …,zn不全为零. 故

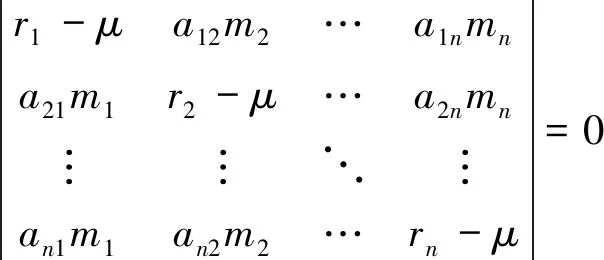
(1)

即μ是矩阵A*的特征值. 因为H的任意相异于λij(i=1, 2, …,n;j=2, 3, …,mi) 的特征值均满足(1). 故矩阵A*的特征值是H的所有异于λij(i=1, 2, …,n;j=2, 3, …,mi) 的特征值.

证毕.

3 等能量图

定理2设G=(V,E)是具有n个顶点的简单图， 对i=1, 2, …,n，Gi和Hi是顶点数为mi的ri-正则等能量图. 则

E(G[G1,G2, …,Gn])=E(G[H1,H2, …,Hn])

证明 设G的邻接矩阵为A(G)=(aij)n×n. 因为Gi和Hi有相同的顶点数mi和度数ri， 由定理1可知，G[G1,G2, …,Gn]和G[H1,H2, …,Hn]有相同的辅助矩阵

现假设A*的特征值的绝对值之和为M且对任意的正整数i(1≤i≤n)，A(Gi)的特征值为ri=λi1≥λi2≥…≥λimi，A(Hi) 的特征值为ri=μi1≥μi2≥…≥μimi. 则

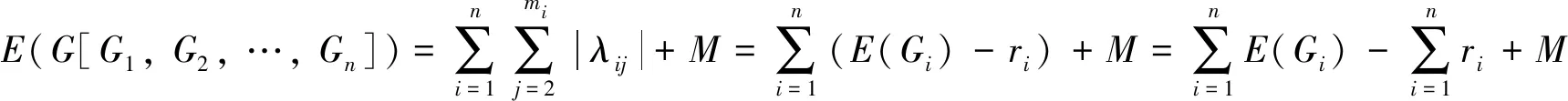
因为E(Gi)=E(Hi)(i=1, 2, …,n)， 所以

E(G[G1,G2, …,Gn])=E(G[H1,H2, …,Hn])

证毕.

4 例子

例1设G是一个图，L1(G)=L(G) 是G的线图， 用递归法可以定义

Lk(G)=L(Lk-1(G)),k≥2

Ramane等证明如下结论[4]:

设G1,G2是两个顶点数为n， 正则度为r≥3 的正则图， 则对任意k≥2，Lk(G1)，Lk(G2)具有相同的能量.

显然，Lk(G1)，Lk(G2)均是正则图， 且它们的顶点数和正则度均相同.

进一步地， Ramane， Gutman等证明如下结论[5]:

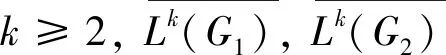
例如G[Lk(G1),Lk(G1), …,Lk(G1)]，G[Lk(G1),Lk(G1), …,Lk(G2)]， …，G[Lk(G1),Lk(G2), …,Lk(G2)]，G[Lk(G2),Lk(G2), …,Lk(G2)] 就是n+1个等能量图.

例2设Kp, p是顶点数为2p的完全二部图，P是Kp, p的完美匹配， 则Kp, p-P和Kp∪Kp都是顶点数为2p， 度为p-1 的正则图. 可以证明[6]:Kp, p-P和Kp∪Kp具有相同的能量4(p-1). 对任意一个顶点数为n的简单图G， 由定理2可知，G[Kp, p-P,Kp, p-P, …,Kp, p-P],G[Kp, p-P,Kp, p-P, …,Kp, p-P,Kp∪Kp], …,G[Kp, p-P,Kp∪Kp, …,Kp∪Kp],G[Kp∪Kp,Kp∪Kp, …,Kp∪Kp] 是n+1 个等能量图.