ANN模型对自热式固定床气化的动态过程预测

黄元晨， 沈元兴， 沈 英

(福州大学机械工程及自动化学院， 福建 福州 350108)

0 引言

固定床生物质气化是一个不稳定的非线性过程， 对其建模的方法主要包括动力学模型、 平衡模型以及神经网络模型. 动力学模型利用数学动力学方式描述气化过程的动力学机制， 考虑各种化学反应以及反应中的相变， 一定程度上提升了对气化机理的认知[1]. 但是气化反应过程复杂， 动力学模型无法全面考虑所有可能的化学反应， 同时对反应系数和动力学常数计算未必准确， 不适合气化炉在线过程控制[1]. 依据气化过程的质量和热平衡构成的模型称为平衡模型， 平衡模型基于化学反应， 综合考虑气化过程的吉布斯自由能最小化和热力学第二定律[2]. 其优点在于不受气化炉的类型和结构的影响， 适用于特定运行参数下气化炉性能的预测， 同时模型易于实现快速收敛. 但是只能预测特定的气化过程， 无法解决实际生产过程中合成气动态变化的滞后性， 对气化过程实时预测不够准确. 人工神经网络(artificial neural network,ANN)能够解决气化预测滞后问题， 以及提升建模的效率. 近些年， ANN建模方法被广泛用于工业过程参数的预测和复杂条件下的过程控制[3].

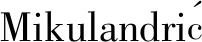
综合考虑气化炉顶部、 中部、 底部温度， 空气流速、 蒸气流速、 反应时间以及催化剂(生物炭)添加量为模型的输入， 通过大量实时采集的数据， 实现更加精准的合成气浓度动态过程预测. 目前大部分研究以气化的静态预测模型为主， 且预测效果欠佳. 本文在考虑多参数的情况下， 建立自热式固定床气化过程合成气动态神经网络模型来实现对气化过程更精准的预测， 从而对气化的操作参数进行优化和过程控制.

1 ANN模型与方法

随着人工智能技术的发展， 有超过100种神经网络模型， 常见的有BP神经网络、 RBF神经网络、 Hopfield神经网络以及Elman 神经网络. BP神经网络的计算过程包括正向传播和反向传播. 正向传播过程， 输入模式从输入层经隐藏层逐层处理， 并转向输出层， 每层神经元的状态只影响下一层神经元的状态[10]. 如果在输出层不能得到期望的输出， 则转入反向传播， 将误差信号沿原来的连接通路返回， 通过修改各神经元的权值， 使得误差信号最小. BP神经网络比其他网络结构简单、 计算量小、 适用性广， 适合工业农业生产模型的建立[11].

2 生物质气化BP神经网络模型建立

2.1 建模数据的筛选

建立气化过程的神经网络模型， 必须获得大量的原始试验数据. 气体传感器每分钟实时采集H2、 CO、 CH4和CO2四种气体的实时浓度， 同时气化炉顶部温度TC1、 中部温度TC2、 底部温度TC3三个温度传感器分别记录气化炉上、 中、 下三个位置的温度变化， 1 599组实验数据为建立模型提供了数据保障. 此外实验数据中被添加300组误差不超过5%的人工随机噪声， 以避免训练极小值. 为保证模型的准确性和泛化能力， 本次研究随机选择8批数据进行人工神经网络模型的训练， 剩余的两批数据(试验组3和8)用于可预测性验证[12]. 每组气化条件对应的设置如表1所示.

表1 气化试验条件设置

注： 上标“a”表示为该实验条件下的的峰值温度.

2.2 两种结构神经网络模型的建立

模型的输入包括7个变量， 分别为TC1、 TC2、 TC3、 空气流速、 蒸气流速、 反应时间以及生物炭添加量. 在这些输入的参数中， 空气流速、 蒸气流速和生物炭添加量在试验过程中是可控制的关键参数， 除此之外， TC1、 TC2、 TC3也是被实时采集的. 传统意义上气化炉温度都被当做模型的输出， 实际操作中发现气化炉的温度检测是比较容易实现的， 然而对气体成分实时检测和动态预测不仅难度大而且成本高， 此外温度是反映气化反应强度的重要指标， 因此也被作为模型的输入. 较少有文献提及ANN模型的最优隐藏层层数和最优隐藏层神经元个数， 因此本文分别对气化过程建立了两类神经网络结构： 一个是单隐藏层， 另一个是双隐藏层， 如图1所示， 并对其预测效果进行测试.

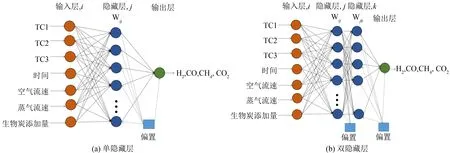
图1 两种结构BPANN模型结构示意图Fig.1 Schematic diagram of the two kinds of structured BP ANN model

为了优化隐藏层和输出层激活函数， 在隐藏层中使用Sigmoid函数(Tansig)与Logarithmic Sigmoid函数(Logsig)， 输出层的激活函数选用线性函数(Purelin)进行训练和测试. 神经网络模型输出层传递函数输出范围设置在-1到1之间， 其中β为常数.

(1)

2.3 神经网络模型的评价

用均方根误差(RMSE)、 相关系数(R2)和平均绝对百分误差(MAPE)分析方法来确定网络的训练和测试性能. 其中，N是样本数，Ti是目标(实际)值，Oi是输出(预测)值. RMSE值越小和R2值越大时， 说明ANN的预测结果具有很好的回归性. 在本研究中， ANN模型使用神经网络工具箱在MATLAB(R2014a， MathWorks)环境中进行训练(nntool).

(2)

3 生物质气化BP神经网络模型修正与预测

3.1 模型结构与参数的修正

如图2所示， 增加训练步数与神经元个数， 可有效减少训练误差MSE， 在两层隐藏层结构中尤为显著. 虽然一定程度的增加神经元个数和训练步数可以提高预测的准确性， 但是会带来计算时间上的增加. Del等[13]提出的“掣肘规则”可用来解释这一问题： 神经网络模型的结构设计， 应当和其对应的作用与适用场合相吻合， 如果可以满足预测要求， 简单的结构和适当的迭代次数可以减少训练时间.

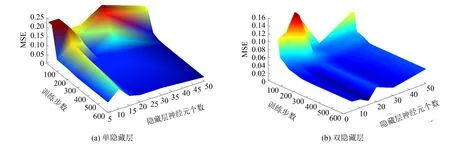
图2 两种ANN结构掣肘规则Fig.2 Ebow rule of the two kinds of ANN model

不同的隐藏层数与不同的神经元个数分别对合成气预测的BP神经网络模型如表2所示， 模型的总迭代次数为1 000次， 收敛误差为10-7. 隐藏层中采用Tansig函数的预测效果比Logsig函数的预测效果好， H2与CO适合采用单隐藏层的Tansig函数预测， CH4与CO2适合采用双隐藏层的Tansig函数预测.

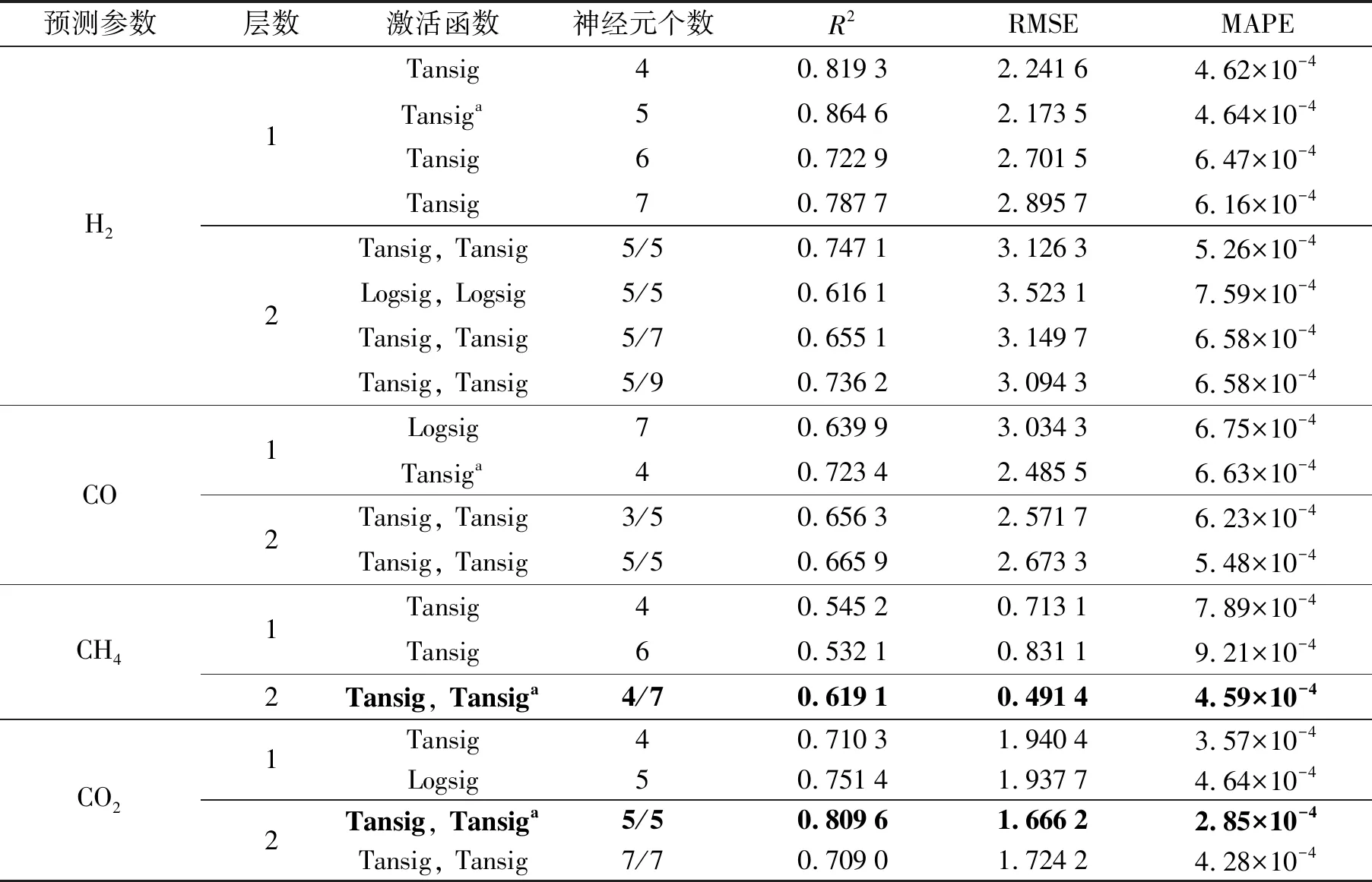
表2 四种气体的ANN的预测结果

注： 上标“a”表示对应用于预测气化性能的较优BP神经网络模型.

3.2 实验结果与预测结果的比较

由表2可知， Tansig函数作为激活函数的隐藏层对H2的预测效果较好， 相对于单隐藏层结构的预测结果， 双隐藏层结构的预测结果并没有明显的优势， 即便增加模型的隐藏层层数可能会提高模型的拟合度， 但是同样可能会导致模型出现“过度适应”， 从而恶化模型的预测能力. 神经元个数为5个的单隐藏层结构对H2的动态预测表现最好，R2可达到0.864 6， RMSE和MAPE值分别为2.173 5和4.64×10-4. 该模型对试验组3和8的预测结果如图3所示， 由图可以看出预测结果与实验结果的吻合度说明本方法对气化炉生成H2的动态建模是准确的. Pandey等[14]利用ANN模型对气化合成气热值预测时， 同样发现单隐藏层结构比双隐藏层表现更加优异.

图3 BP神经网络模型对气化合成气中H2浓度的预测结果Fig.3 Prediction of H2 concentration in syngas by BP ANN model

Tansig函数作为激活函数的隐藏层对CO的预测效果较好， 单隐藏层4个神经元的模型对CO的进行预测， 得到的R2为0.723 4， RMSE与MAPE值分别为2.485 5和6.63×10-4. 利用该模型对试验组3和8的预测结果如图4所示， 预测结果与实际结果较为吻合.

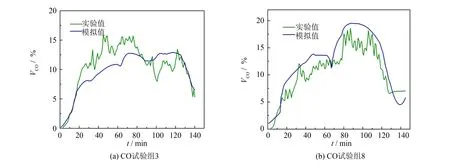
图4 BP神经网络模型对气化合成气中CO浓度的预测结果Fig.4 Prediction of CO concentration in syngas by BP ANN model

由表2加黑部分可知， Tansig函数作为激活函数的隐藏层对CH4和CO2的预测效果较好， 且相对于单隐藏层结构的预测结果而言， 采用双隐藏层结构的预测结果明显更优. 该模型对试验组3和8的预测结果如图5～6所示， 预测结果与实际结果较为吻合.

图5 BP神经网络模型对气化合成气中CH4浓度的预测结果Fig.5 Prediction of CH4 concentration in syngas by BP ANN model

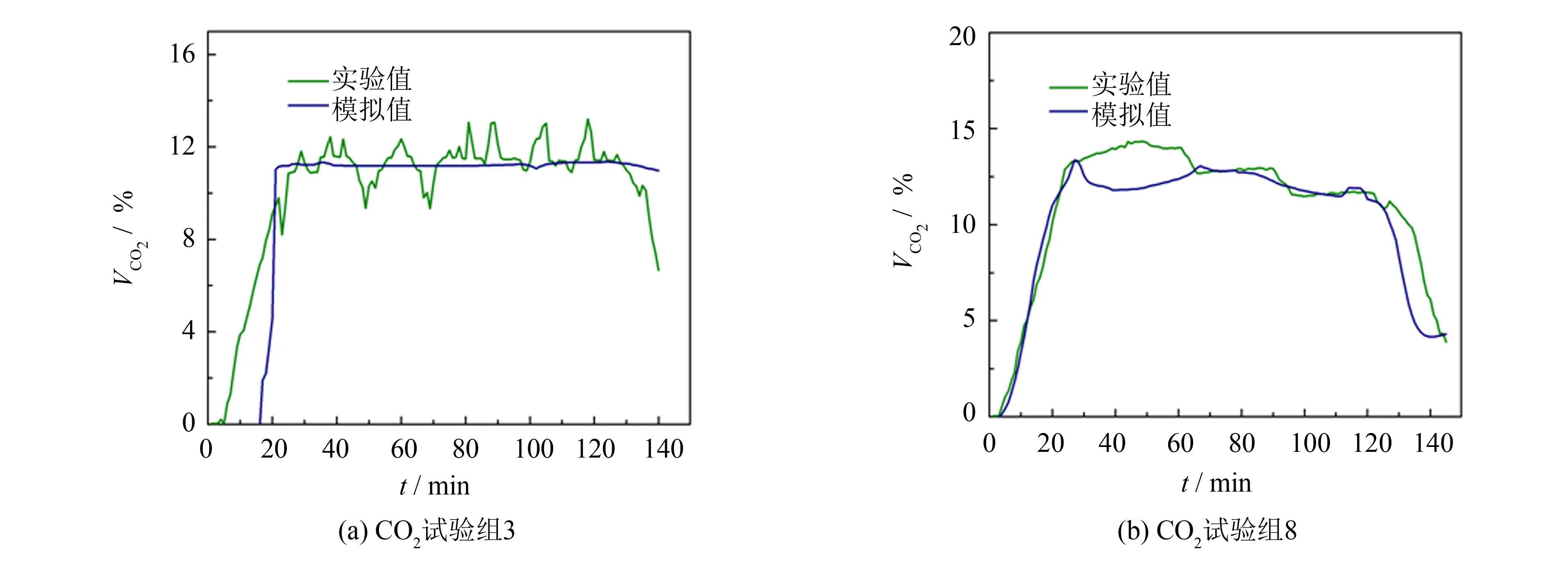
图6 BP神经网络模型对气化合成气中CO2浓度的预测结果Fig.6 Prediction of CO2 concentration in syngas by BP ANN model

4 结语

1) 构建生物质气化的动态过程BP神经网络模型， 可以实现对生物质气化全过程的动态实时预测， 相较于传统的神经网络模型的静态平均值预测， 动态预测模型更加具有连续性和实际运用价值.

2) 本模型考虑的输入量包括气化炉的顶部温度、 中部温度、 底部温度、 空气流速、 蒸气流速、 反应时间以及生物炭添加量， 模型综合考虑的气化影响因素较为全面； 同时1 599组气化数据用来训练模型， 保证了四种主要气体浓度预测模型的准确性和泛化能力， 其中氢气的预测R2可达到0.864 6.

3) 综合考虑“掣肘规则”， 优化模型的最佳迭代步数、 隐藏层层数以及隐藏层神经元个数， 在满足模型训练收敛要求的情况下减少了模型的复杂程度与训练时间.