边界层厚度可变的柔性关节空间机器人两级滑模控制

杨 淼， 陈 力

(福州大学机械工程及自动化学院， 福建省高端装备协同创新中心， 福建 福州 350108)

0 引言

关节在承担空间机器人系统各部件的物理连接、 力矩输出与传递等任务中举足轻重. 传统方法是将其简化为刚性关节， 但实际其内部的谐波装置会使关节产生柔性振动， 从而产生弹性变形势能. 柔性振动带来的问题是， 当关节处电机转子转过一定角度时， 由于弹性力的作用， 关节铰的转动角度与电机转角的大小不一致， 从而导致系统关节转角误差. 目前对关节柔性[1]的研究主要存在跟踪精度低、 收敛速度缓慢、 稳定性不足以及系统不确定性带来的跟踪误差等问题， 为此众多学者展开了深入的研究.

文[2]基于扩展卡尔曼滤波器设计了一种自适应控制方法， 但控制精度不高. 文[3]提出一种递阶控制方法， 将逐步逆向设计与模糊自适应系统相结合， 有效消除了系统不确定性. 陈志勇等[4]在原先模型基础上引入柔性补偿器， 并利用奇异摄动法为关节柔性较大的空间机器人系统进行鲁棒控制. 文[5]同样利用奇异摄动法， 将快变子系统的关节弹性力控制方法与慢变子系统的位置/力控制方法进行组合， 但是该方法的计算较为复杂. 除此之外， 文[6]利用干扰观测器来有效削弱系统抖振， 文[7]在滑模控制的基础上加入模糊控制方法解决系统的振荡问题. 谢立敏等[8]还提出一种轨迹跟踪的鲁棒反步控制方法， 运用速度滤波器来避免对系统速度信号的测量， 从而提高控制精度.

综上所述， 本研究以载体位姿受控的平面两杆柔性关节空间机器人为模型， 主要解决系统跟踪精度低、 收敛速度慢以及稳定性不足的问题, 并提出两级滑模控制方法. 同时， 引入边界层厚度可以调节饱和函数来减轻系统振荡. 最后利用Matlab仿真实验对以上方法进行了验证.

1 柔性关节空间机器人的模型建立

将作平面运动的平面两杆柔性关节空间机器人系统简化为如图1所示的模型.B0为该空间机器人的漂浮基基座，B1、B2则为依次连接在基座上的两个空间机械臂，O1、O2则分别为两个机械臂的柔性关节.

建立下图所示的平动的惯性坐标系(O-XY)及各分体Bi(i= 0, 1, 2)的坐标系(Oixiyi)，Oi(i=1, 2)为联结Bi-1与Bi的转动铰中心.q0为载体基座坐标系相对于惯性坐标系的转角，qi(i=1, 2)为第i根机械臂的实际关节转角，θi(i=1, 2)为第i个驱动电机转子关节处的实际驱动转角.

根据文[9]的假设， 将柔性关节描述为如图2所示的简化模型， 机械臂与安装在其关节处的驱动电机转子之间的柔性联接可简化为一刚度系数为k的线性扭转弹簧. 可以看出， 由于弹簧弹性力的作用， 使驱动电机转子转动角度θi的大小与机械臂关节铰的转动角度qi未能一致， 从而带来转角误差σi.

图1 柔性关节空间机器人 Fig.1 Flexible-joint space robot

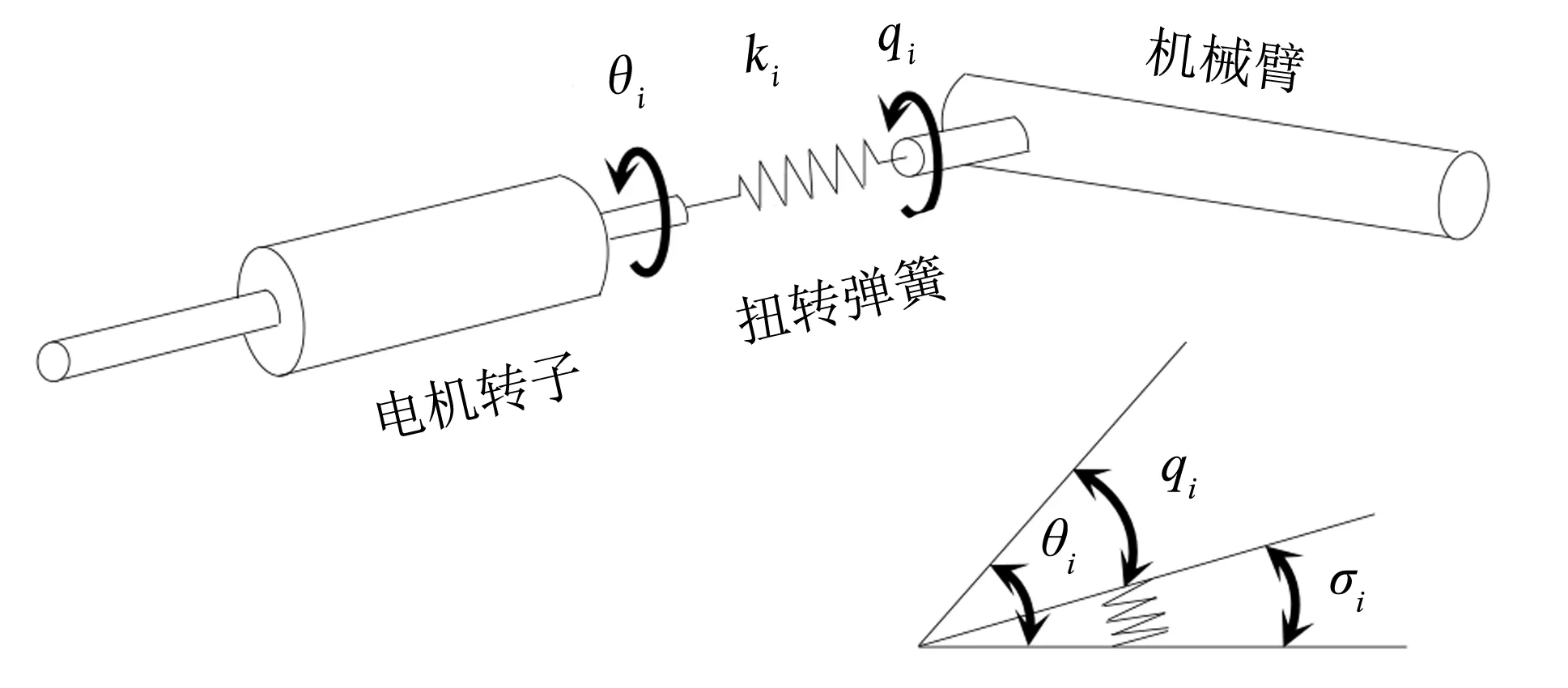
图2 柔性关节的简化线性弹簧模型Fig.2 Simplified linear spring model for flexible joints

由动量守恒定律， 并结合Lagrange方程可推出上述系统的动力学方程：

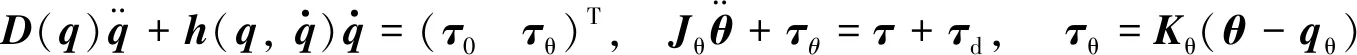
(1)

2 基于奇异摄动理论的系统分解

2.1 快变子系统的控制器设计

基于上述动力学关系所建立的系统模型， 根据奇异摄动理论， 将上述刚柔混合系统分解为快变和慢变两个子系统， 其分别对应柔性运动部分和刚性运动部分， 因此， 系统的总控制方法可表示为

τ=τs+τf

(2)

其中:τs和τf分别为慢变子系统和快变子系统的控制方法.

定义正比例因子ε及正定对角矩阵K1， 它们与柔性关节的刚度系数矩阵Kθ满足如下关系：

(3)

令机械臂关节角qθ为慢变量， 表示关节柔性化弹簧的弹性力zθ=Kθ(θ-qθ)为快变量， 并根据式(3)， 可将上述系统动力学方程表示为如下的另一种形式：

(4)

首先提出基于速度差值反馈的快变子系统的控制方法：

(5)

式中：Kf=K2/ε,K2为正定、 对角参数阵.

由式(5)可见， 针对快变子系统设计了速度差值反馈控制方法. 该速度差值影响到系统的精度， 将其反馈回控制器， 然后通过对前面的参数系数矩阵Kf的调节来实现对该系统的控制.

将式(2)和式(5)代入式(4)后可得到如下快变子系统的动力学方程：

(6)

(7)

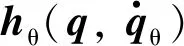
2.2 边界层厚度可变的两级滑模控制器设计

2.2.1构造两级滑模面

为漂浮基柔性关节机械臂系统设计了两级滑模面， 首先利用机械臂柔性关节转角及其角速度和驱动电机转角及其角速度设计了一级滑模面s1和s2， 然后在该滑模面的基础之上利用系数构造了第二级滑模面：

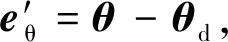
(8)

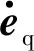
然后， 由第一级滑模面构造第二级滑模面

s=ms1+ns2

(9)

式中：m和n为大于0的常数；s∈R3为构造的第二级滑模面.

2.2.2设计滑模控制律

为提高系统收敛速度以及解决系统振荡问题， 利用幂次函数快速收敛的特性构造了趋近律， 然后又引入边界层厚度可变的饱和函数来消除振荡， 故将控制律设计为

(10)

引入如下边界层厚度可变的饱和函数：

(11)

该函数将控制部分分为两段， 在边界层外部采用阶跃变化的切换控制， 在边界层内部则采用连续的线性化控制. 式中： 参数β即为边界层厚度；β的大小则会直接影响系统的连续性、 稳定性以及控制精度.

该可变边界层[10]的控制策略在于可以通过调节边界层厚度的大小来实现两段函数的来回切换， 系统先达到较大的边界层， 当误差减小到一定值ek时， 切换到小边界层. 可变边界层的厚度表达式为

β=(1-ε)β1+εβ2

(12)

式中： 当|eq|>ek时，ε=1； 当|eq|≤ek时，ε=0. 另外， 设β2的最大值为β20. 为使误差减小得更快， 转速曲线更为平滑， 当|s|>β20时，β2=β20； 当|s|≤β20时，β2=β20exp(-at)， 其中a为速率调节系数.

对式(8)两边同时求导得

(13)

同时， 对式(9)两边求导并令其为零， 即

(14)

将式(13)代入式(14)， 并结合式(1)可得

所以移项解得

(15)

将式(15)代入式(10)解得控制力矩为

其中： 载体姿态控制力矩τ0为τ′的第一行； 慢变子系统控制力矩τs为τ′的第二行和第三行组成的列向量.

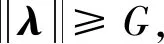
证明 选取李雅普诺夫函数如下， 并对其求导得：

(17)

将式(14)代入得：

再将式(16)代入式(18)得：

同理， 又有：

从而得：

(20)

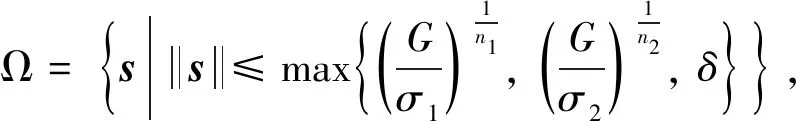
3 仿真与分析

为验证所设计的控制器的可行性和有效性， 以图1所示的平面两杆机械臂模型为例， 利用快变子控制律式(5)、 慢变子控制律式(16)以及总控制律式(2)进行了系统仿真.

选择系统惯性参数的真实值如下：m0=40 kg，m1=2m2=2 kg，l0=1.5 m，l1=l2=3 m； 中心惯量矩为：J0=34.17 kg·m2，J1=1.5 kg·m2，Jθ1=Jθ2=0.07 kg·m2； 扭转弹簧系数为：Kθ1=Kθ2=500 N·m/rad. 在控制器设计中选择待设计的正参数：λ1=λ2=30，λ=diag(10, 10, 10)； 滑模面系数为：m=30，n=0.3； 控制律系数为：σ1=20，σ2=18； 趋近律的幂次为：n1=10，n2=0.5； 其他参数取为：δ=0.005，ek=0.2，β1=0.5，β20=3，a=10.

假设电机侧扰动是由正常值干扰和两种频率周期性干扰组成的混合信号， 即：

选取基座姿态角、 关节角1和关节角2的期望轨迹分别为：

系统仿真时间为15 s， 仿真结果如图3～6所示.

为了说明该方法的优越性， 在同样系统模型、 相同的初始条件、 系统参数和外部干扰的情况下， 将本文提出的两级滑模控制方法与传统滑模控制方法进行比较. 图3表示两级滑模控制律下基座姿态角和两机械臂关节转角轨迹跟踪曲线图， 图4表示两种控制方法关节角误差对比图.

图3 关节轨迹跟踪曲线图 Fig.3 Joint trajectory tracking curve

图4 关节误差对比图Fig.4 Joint error contrast diagram

结合图3和图4可以看出， 在本研究所提出的两级滑模控制方法下， 基座姿态角与关节角能够在1～1.5 s快速收敛到期望轨迹， 而传统滑模需要4～5 s才能收敛， 所以两级滑模控制方法的收敛速度较传统滑模要更快； 另外， 从以上两图收敛后的轨迹来看， 两级滑模的实际轨迹能够与期望轨迹完全重合， 关节误差基本趋近于零， 而传统滑模的关节误差则有一定的偏差， 说明两级滑模控制方法的跟踪精度更高.

图5和图6分别为三关节的驱动力矩图以及两柔性关节驱动电机转子的转角图. 由图5可以看出， 输入力矩在2 s以内趋于稳定且变化幅度很小， 这与前面的轨迹跟踪图的效果吻合， 且输入力矩基本没有抖振， 充分说明了边界层饱和函数替代符号函数后达到了消除抖振的效果. 图6为驱动电机转子的转角图， 也是在2 s以内趋于正常状态， 且能在一定区域内保持稳定状态.

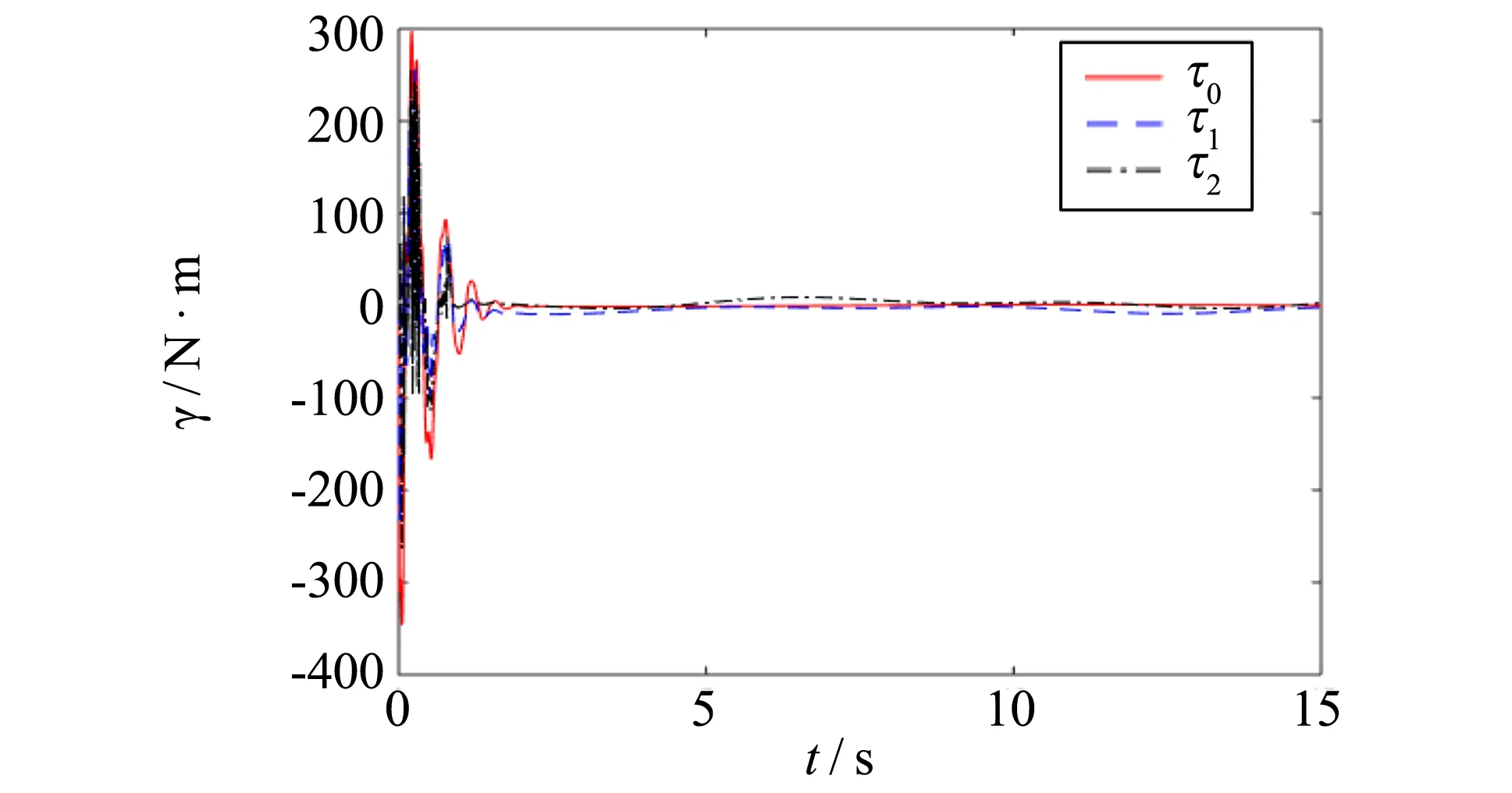
图5 关节驱动力矩图 Fig.5 Joint drive torque diagram

图6 驱动电机转子转角图Fig.6 Drive motor rotor angle diagram

4 结语

1) 根据分级滑模控制思想设计了两级滑模面， 提高了关节轨迹的跟踪精度. 另外， 在滑模控制项中引入了多幂次趋近律提高了关节轨迹跟踪的时间， 使各个关节能够快速收敛到期望轨迹.

2) 在滑模控制器设计中， 利用可变边界层的饱和函数替代符号函数， 有效消除了控制力拒的抖振， 实现了柔性关节机械臂的快速、 高精度的跟踪控制.