2019年高考数学立体几何专题解析

天津师范大学教育学部 (邮编：300387)

天津市第四十三中学 王利群 (邮编：300110)

1 引言

高中数学立体几何内容包括立体几何初步、空间向量与立体几何两部分，是高考数学的必考内容之一.总览《普通高中数学课程标准(2017年版)》(以下简称课程标准)和《2019年普通高等学校招生全国统一考试大纲的说明》(以下简称考试大纲)后发现，立体几何专题内容主线突出，以核心知识为重点、以基本图形为载体、着重考查空间中点、线、面的位置关系的判断和证明，以及空间角、几何体的表面积和体积等几何量的计算，突出体现了对数学学科核心素养——直观想象、逻辑推理、数学运算、数学抽象的考查[1].

对2019年13套高考数学试卷中立体几何试题进行全面分析和研究，力图准确把握其命题特点和趋势，以期对高中的数学教学和学习提供参考.

2 试题特点

2.1 题量、题型和分值相对稳定

总览13套试卷发现每套试题基本上以“一小题一大题”或“两小题一大题”的形式出现，分值稳定在17-22分之间，考查题型涉及选择题、填空题和解答题.其中，解答题以常见的空间几何体为载体，考查方式、方法相对固定，选择题或填空题需要学生想象并构建几何图形，考查画图能力，是对解答题的有效补充，使立体几何问题呈现重点突出、考査全面、形式多样、解法灵活等特点[2].值得一提的是，为了与《普通高中数学课程标准(2017年版)》(以下简称课程标准)的要求相吻合，2019年高考命题大幅度减弱对三视图这一题型的考查，除北京卷和浙江卷外，其余地区均未考查三视图.

2.2 考查内容集中，重点突出

高考立体几何试题考查内容集中，重点突出.考点多集中在空间几何体体积、距离、空间角、点、线、面位置关系的证明以及运用向量法研究空间基本图形的位置关系和度量关系等方面.

从题型来看，锥体、柱体、球体等空间几何体的体积、点到面的距离的计算是选择和填空题考查的重点；解答题一般有两至三问(天津卷和北京卷有三小问)，除上海卷外(线面夹角)，第一问均考查线面、面面平行或垂直的证明，通常考查学生运用综合几何法解决问题的能力.理科第二问注重对空间角，如线面角、二面角的考查，尤其是二面角的正弦值和余弦值，旨在考查学生运用向量法解决立体几何问题的能力，体会向量方法的作用；文科第二问一般求体积、面积和点到面的距离.此外，北京卷的第三问考查了探索性问题，探索使结论成立的条件，对学生空间想象能力和运用数学知识、方法，分析问题、解决问题的综合数学能力要求较高.

2.3 文、理科试题一致性较强

2019年13套高考数学立体几何试题中，除上海卷和浙江卷文、理不分科外，文、理科试题差异着重体现在解答题第二问上.对于文、理分科的试卷，除全国I卷之外，其他试卷中立体几何文、理科选择题与填空题均相同，个别试卷题号不同；除天津卷外，其他试卷的立体几何试题解答题题目和第一问均相同，且江苏卷文、理科解答题完全相同.这体现了新课改的理念，为逐步全面实施新课改，文、理不分科作铺垫.

3 试题举例分析

3.1 线、面平行或垂直关系

高考对点、线、面位置关系的考查重点是证明直线、平面平行或垂直关系，一般在解答题第一问中.解决这类问题的基本思想方法是转化，即将三维空间直线与平面、平面与平面的位置关系转化为二维直线与直线的位置关系.解题的关键是熟练掌握直线、平面平行或垂直的定义、判定定理和性质定理.图1是点、线、面位置关系的结构图，显示了空间直线、平面平行或垂直关系之间的转化.

图1 点、线、面位置关系结构图

例1 (北京卷·理12)已知l、m是平面α外的两条不同直线，给出以下三个论断：①l⊥m；②m//α；③l⊥α.以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：______．

解析三个命题中选出两个作为条件共有3种选法，即此题可能的答案有3种.利用直线、平面平行的垂直的性质定理和判定定理确定正确的组合.

若①②，则③.当l⊥m，m//α时，直线l与平面α的位置关系不一定是l⊥α，还可能斜交或平行.故命题不成立.

若①③，则②.由l⊥m及直线m在平面α外可知，有且只有一个平面β经过直线m且垂直于直线l，又因为l⊥α，所以α∥β，所以m//α.

若②③，则①.作经过m的平面β，设β∩α=n.由m//α可知m//n.又因为l⊥α，所以l⊥n，所以l⊥m.命题成立.

评析本题主要考查点、直线、平面的位置关系，学生需要熟练掌握直线和平面平行或垂直的判定定理和性质定理，从三种可能命题中找出正确的命题.

例2 (全国卷II·理7)设α、β为两个平面，则α∥β的充要条件是( )

A.α内有无数条直线与β平行

B.α内有两条相交直线与β平行

C.α，β平行于同一条直线

D.α，β垂直于同一平面

答案：B.

解析根据面面平行的判定定理(如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行)可知，A选项中的无数条直线可能不相交，所以A错，而C、D选项中的两个平面都可能相交，所以C、D错，因此A、C、D选项都不是α∥β的充分条件，B选项是α∥β的充要条件.

评析本题以逻辑用语的形式考查面面平行的性质定理和判定定理，需要学生熟练地掌握这些定理以及定理的逆定理.由于本题是一道选择题，所以可通过举反例快速解答.

3.2 空间几何体

此类型题一般出现在选择、填空题或文科解答题的第二问中，多考查内切、外接组合体的表面积和体积.这些组合体多是由图2中基本图形组合而成，例如棱锥的内切球、内切圆柱、棱锥或棱柱的外接球等.解题关键是要正确画出相应的几何图形，厘清各几何体之间的内在联系，通常将图形放在长方体、正方体或球中，利用其特性解题，主要考查学生直观想象和数学运算素养.

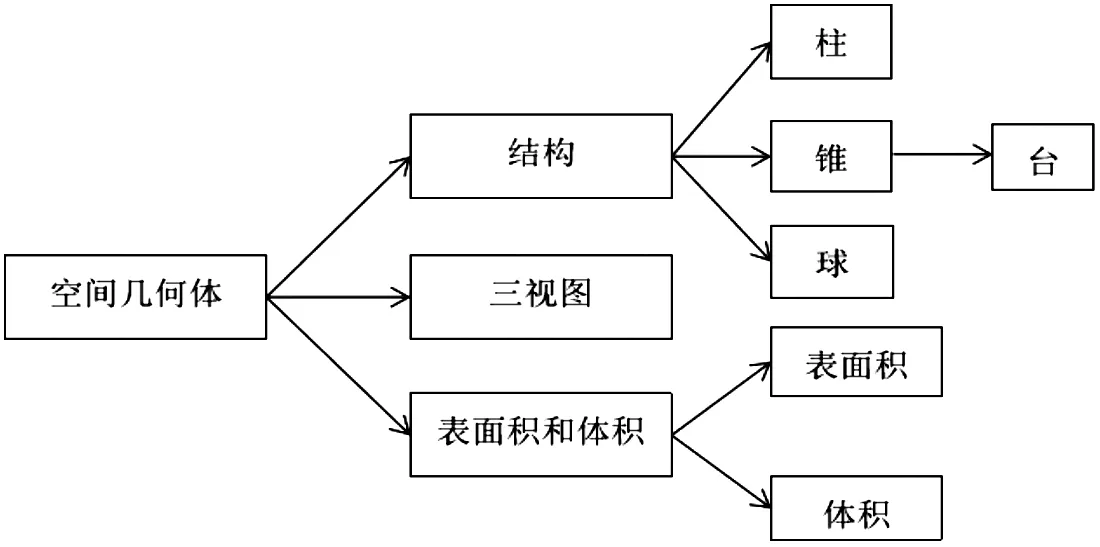
图2 空间几何体知识结构图

例3 (全国I卷·理12)已知正三棱椎P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E、F分别是PA、AB的中点，∠CEF=90°，则球O的体积为( )

图3

图4

解析方法1：先根据正三棱锥性质和已知条件证明正三棱锥三条棱两两垂直且相等(如图3)，将其视为正方体的一角，在正方体中再根据勾股定理求出球的半径，最后根据球的体积公式求出结果(如图4).

方法2：利用余弦定理求出三条侧棱的长，由已知可得三条侧棱两两垂直且相等，故球是以三条侧棱为棱的正方体的外接球，所以正方体的体对角线即为球的直径，根据球体积公式求出结果.

方法一：因为三棱锥P-ABC为正三棱锥，所以PB⊥AC，PC⊥AB.

又因为E、F分别是PA、AB的中点，所以EF//PB.

因为∠CEF=90°，所以PB⊥EC，又AC、EC⊂平面PAC，AC∩EC=C

所以PB⊥平面PAC.所以PB⊥PA，PB⊥PC.

又因为PB∩AB=B，PB、AB⊂平面PAB，所以PC⊥平面PAB.

所以PC⊥PA.

又因为PA=PB=PC，所以PA、PB、PC两两互相垂直且相等，可视为正方体一角.

方法二：如图3，设∠PAC=θ，PA=PB=PC=2x，EC=y，

以下解法同方法一.

评析本题是选择压轴题，主要考查学生空间想象能力和运算能力.学生可以利用综合几何法或余弦定理进行求解.解决此类题目主要有两种方法：一是将其放在长方体或正方体中，根据体对角线即为球的直径求解；二是确定球心的位置，根据球的性质求解.两种方法都需要准确理解空间几何体的定义，切实把握空间几何体的结构特征，根据已知条件，构建几何模型，在几何模型中求解.

3.3 空间角和距离

空间角问题主要包括异面直线所成角、线面所成角和二面角三种(结构较明确，不再附加结构图)，多出现在填空题和解答题中，学生可以选择向量法或综合几何法，利用化归思想将空间角转化为线线角求解.有关距离的计算多是求点到平面的距离，一般出现在理科选择或填空题，文科的解答题中.

例4 (浙江卷·8)设三棱锥V-ABC底面是正三角形，侧棱长均相等，P是棱VA上的点(不含端点)，记直线PB与直线AC所成角为α，直线PB与平面ABC所成角为β，二面角P-AC-B的平面角为γ，则( ).

A.β<γ，α<γB.β<α，β<γ

C.β<α，γ<αD.α<β，γ<β

答案：B.

图5

解析先要根据已知条件画出正三棱锥，再根据定义确定异面直线成角、线面成角、二面角的平面角(如图5)，最后根据空间几何体的性质、定理表示出各个角的正弦值，利用正弦函数的性质比较角的大小.

过点P作PD//AC交VC于D，则α=∠BPD.连接BD，因为三棱锥底面为正三角形，VA=VB=VC，所以V-ABC为正三棱锥，所以BD=PB.取PD的中点E，连接BE，过点E作EH⊥平面ABC于点H，连接BH.

过点P作PF⊥平面ABC于点F，连接BF，则β=∠PBF；

作PG⊥AC于点G，连接GF，则γ=∠PGF.

又因为PD//AC，E在PD上，EH⊥平面ABC于点H，PF⊥平面ABC于点F，

则sinα>sinβ.

所以α>β.

由对称性BP=CP，而CP>PG，

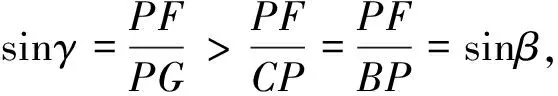
则α>β，γ>β.

评析这道题囊括了三种类型的空间角.解决此类问题难点有两个：一是准确地寻找空间角；二是构建空间角之间的关系.因此，学生首先要熟练掌握空间角的定义，根据已知作出线线角、线面角和二面角的平面角，然后构造直角三角形，根据三角函数的定义，用三边表示各个角的函数值，最后利用边的大小关系以及三角函数的性质确定角的大小关系.上述解题方法为通性通法，但比较费时，考虑到本题题型和题中几何体(正三棱锥)的特殊性，学生可选择其他方法和策略解题.例如利用极限思想，将P点无限逼近V点，再利用正三棱锥及三角函数的性质解题或或者采用特殊化的方法，如取棱VA的中点为P，通过具体计算确定选项.

3.4 立体几何中的向量方法

空间向量能够表示点、直线、平面等元素，建立空间向量和空间图形之间的联系可以将立体几何问题转化为空间向量问题，利用空间向量的运算加以解决.如图6所示，空间向量语言可以表述直线与直线、直线与平面、平面与平面的夹角、距离以及垂直与平行关系，因此可以利用向量方法证明直线、平面间垂直与平行的关系，解决点到直线、点到平面、相互平行的直线、相互平行的平面的距离问题以及简单夹角问题.

图6 空间向量与立体几何结构图

图7

图8

图9

例5 (全国卷III·理19)图7是由矩形ADEB，Rt△ABC和菱形BFGC，组成的一个平面图形，其中，AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连接DG，如图8.

(1)证明图8中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；

(2)求图8中二面角B-CG-AD的大小.

解析(1)由两条平行线确定一个平面，证明四点共面；由已知平面中的垂直关系证明面面垂直.(2)建立直角坐标系(如图9)，利用向量法求出两平面法向量夹角的余弦值，进而求出二面角的大小.

(1)由题意得AD//BE，CG//BE，所以AD//CG，即AD，CG确定一个平面，所以A，C，G，D四点共面.

由已知得AB⊥BE，AB⊥BC，所以AB⊥平面BCGE.又因为AB⊂平面ABC，所以平面ABC⊥平面BCGE.

(2)作EH⊥BC垂足为H.

因为EH⊂平面BCGE，平面ABC⊥平面BCGE，所以EH⊥平面ABC.

评析本题将平面图形翻折问题和立体几何相联系，有别于常规题目呈现方式，学生要知道平面图形翻折后各构成元素变与不变的关系，利用“不变性”解题. 解题方法和程序与常规题目并无差别：利用面面垂直性质证明两平面垂直，运用向量法求出二面角的余弦值，进而求出二面角大小.

4 启示

4.1 重视基本图形，提炼本质特征，发展直观想象素养

立体几何研究现实世界中物体的形状、大小和位置关系.对于学生来说，空间几何图形复杂、要素较多，难以发现它们之间的相互联系.因此，要以基本立体图形，比如长方体为载体，帮助学生认识和理解空间点、直线、平面的位置关系，抽象出定义，并通过直观感知，归纳空间中直线与平面平行或垂直的性质定理和判定定理[3].在教学过程中，可以充分利用实物、计算机软件等让学生观察基本立体图形，利用的生动性与形象性来直观清晰地描述与分析数学问题，实现抽象思维与形象思维之间的转换，将复杂的数学问题简单化.[4]以此建立数与形之间的联系，感知、领悟各种空间几何体的关系，提炼其本质特征，构建数学问题的直观模型，发展直观想象的数学素养.

4.2 突出内容主线，聚焦重点题型，把握内在逻辑联系

高考立体几何试题内容聚焦，重点突出.主要考点包括：直线、平面平行或垂直的证明；空间几何体表面积、体积、空间角、距离的度量计算；空间向量在立体几何中的应用等.教学应遵循从整体到局部、从具体到抽象的原则构建立体几何的研究路径.(1)从对空间几何体的整体观察入手，认识空间图形的结构特征、平面表示，掌握其面积和体积的计算；(2)在此基础上，抽象出构成空间图形的基本元素——点、直线、平面，借助长方体直观感知其位置关系；(3)重点研究直线、平面的特殊位置关系——平行和垂直的判定和性质[5]；(4)运用空间向量研究空间基本图形的事物位置关系和度量关系(空间角)，体会向量法和综合几何法的共性和差异，感悟空间向量在处理立体几何中的工具作用.在日常教学中，教师要从整体上进行教学设计，突出内容主线，既要注重概念学习，又要注重学科的结构体系，凸显知识的内在逻辑关系，学生只有真正理解这些内容之间联系，才能更有序更有逻辑地去研究新内容，达到本质认识[6].

4.3 凸显思想方法，总结通性通法，提升问题解决能力

学习立体几何的基本方法是直观感知(识图)——操作认识(画图)——度量计算(算图)——思辨论证(证图)[5].解题时，往往依据四个基本事实，将空间图形问题转化为平面图形问题进行求解.因此，立体几何问题重点考查数形结合、转化与化归的数学思想方法.向量方法和综合几何法是研究空间几何问题的两种方法.向量方法将几何问题转化为代数问题，通过向量运算研究空间几何体的位置关系(平行、垂直)和度量关系(空间角、距离)；综合几何法根据基本事实、判定定理和性质定理研究空间几何问题.教学中要根据题目类型总结解题的通性通法，让学生在练习中不断摸索解题方法和规律，积累数学学习经验，并以此不断促进对知识方法的理解，对核心内容的掌握，提升学生解决实际问题的能力.同时，要渗透探究创新性题目，达到对知识的灵活运用.

4.4 注重解题规范，正视语言表述，提高逻辑的严谨性

对空间几何体性质的刻画有图形语言、文字语言和符号语言三种类型.图形是从实物和模型第一次抽象的产物，也是形象、直观的语言；文字是对图形的描述、解释与讨论；符号则是对文字语言的简化[5].在描述立体几何的定义、定理、性质时，开始借助集合语言描述几何对象之间的关系，学生比较陌生[5].教材分析者亲历把教材内容从静态形式激活到动态形式，再沉淀为静态形式的过程，实现教材话语体系向教师话语体系转化，以及教师话语体系向学生话语体系转化的递进顺序[7].教学中要通过对图形的观察和操作，引导学生发现和提出描述基本图形平行、垂直关系的命题，逐步学会用准确的数学语言表达这些命题，直观解释命题的含义和表述证明的思路[3]，熟练地掌握三种语言的相互转化，帮助学生有逻辑地思考和表达.同时，要注重解题书写的规范性，给予示范引领，提高逻辑的严谨性，发展逻辑推理的数学学科核心素养.