基于角点PRM的移动机器人路径规划

宋 宇, 王志明

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

随着自动机器人技术的发展，近年来路径规划算法得到越来越多的国内外学者关注，路径规划的相关算法层出不穷，从蚁群算法、A*算法[1]、D*算法、RRT算法、PRM算法、人工势场法到模糊逻辑算法、神经网络算、强化学习算法，其中PRM算法由于相对于A*算法用时较少得到广泛应用，但由于传统PRM算法存在窄通道连通率低的缺陷。基于高斯采样[2]的PRM算法增加了窄通道连通率，但由于高斯采样得到的点大多数集中在障碍物边缘线上，而障碍物边界点大多并不是产生最终路径所经过的点，导致后续点与点之间的连通性检测花费时间成倍增加。基于桥测试采样[3]的PRM算法增加了路径连通率，但由于桥测试采样产生的是由两个在障碍物中的点的中点位置得到的，导致基于桥测试采样的PRM算法只适用于通道宽度变化不大的情形。文献[5]提出了利用人工势场力将落在障碍物中的点移动到自由空间的方法，提高了采样点的利用率。由于真正对最终路径起决定性作用的点是障碍物的角点，故文中提出了一种结合角点检测的PRM算法。仿真结果表明，改进算法在窄通道场景与普通场景下，消耗时间与路径长度都得到了较好的结果。

1 Harris角点检测算法

文中所采用的Harris角点检测算法步骤如下:

1)计算图像的水平、竖直灰度值变化量矩阵Ix，Iy。文中采用了高斯函数求微分，即用Fx矩阵与Fy矩阵分别与原图像的像素矩阵作卷积得到Ix与Iy。

(1)

(2)

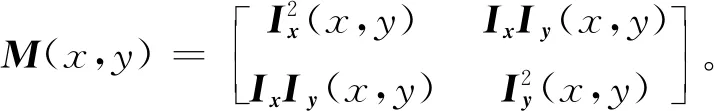
(3)

3)计算图像中所有像素的R值

R(x,y)=detM(x,y)-

k*(traceM(x,y))2。

(4)

4)对于上述得到的R矩阵，分别判断每个像素的R值是否同时大于这个像素的8个邻居像素的R值，若都大于，则此像素所在的位置为角点。

2 改进PRM算法

2.1 采样点的选择

1)首先采用Harris角点检测算法检测到图像中所有角点，然后从检测到的所有角点中排除距离过近的角点。即为了排除1个实际角点附近产生了许多输出角点的情况，文中在使用Harris角点检测算法的过程中，对新选择的角点加了距离限制条件，若新产生的角点与之前产生的所有角点的最小距离小于给定阈值k(文中取k=10)，则此新角点不计入最终角点内。

2)为了增加角点之间的连通性，在Harris产生出n个角点后，以每个角点为中心，上下左右各产生距离每个角点d(文中取d=10)的4个临近点，即若第一步产生的角点数量为n，此时额外产生4n个点，然后从这4n个点中保留不在障碍物中的点作为最终输出点。

2.2 Cardinal 样条曲线路径平滑

样条曲线是通过在给定点之间内插点的方式实现的，文中采用的是Cardinal 样条曲线。单段Cardinal 样条曲线是由4个给定点确定的，如图1所示。

图1 Cardinal 样条曲线

图中:P0，P1，P2，P3为给定的4个点，u为一个从0增加到1的参数，u从0取到1对应得到P1到P2之间的所有内插点，点P1与P2之间的内插点是由下式得到的：

(5)

(6)

其中，s=1-t/2，t为tension系数。由于每段Cardinal样条曲线在分段点处一阶导数连续，故给定n个控制点，可得到一条由n-3段Cardinal样条组合成的一条光滑曲线。

3 仿 真

3.1 路径长度与消耗时间对比

使用Matlab 2014a在cpu为i3-2120，3 G内存，32位Windows7的电脑上进行了仿真，给定500×500像素的地图下改进算法与传统PRM算法、高斯采样PRM、桥测试采样PRM的路径图，起点坐标为[10,10]，终点坐标为[490,490]，由于文中改进算法加入了角点检测过程，故不需要额外设置参数，传统PRM算法、高斯采样PRM、桥测试采样PRM的采样点数设置为固定值100，桥测试采样中的其他参数经反复测试设置为较优参数。不同地图算法路径对比如图2所示。

(a) 地图1

(b) 地图2

(c) 地图3

(d) 地图4图2 不同地图算法路径对比

从图2可以看出，由于改进算法采用的是角点，而桥测试算法得到的点大多为通道的中点，高斯采样得到的多数点为障碍物边界，故改进算法得到的路径长度最短。

各算法在路径长度和运行时间方面的结果对比见表1。

由表1可以看出，当给定地图总的角点数量不多时(如地图4)，改进算法产生的最终点个数较少，导致后续用于点与点之间的连通性检测的时间(相比于其他3种算法给定100个点)有所减少。同时由于改进算法产生的4n个点中，每4个点相对距离较近，用于这些点之间连通性检测的时间也相对较少，故改进算法虽然加入了角点检测的过程，但算法效率反而较高。

算法在每种地图下100次实验路径连通性对比见表2。

表2 100次实验算法连通次数表

3.2 Cardinal 样条曲线路径平滑

以起点、终点以及A*算法得到的所有路径点为Cardinal 样条曲线中的控制点，文中tension系数设置为0.8，经Cardinal 样条平滑后得到路径如图3所示。

(a) 地图5

(b) 地图6图3 Cardinal 样条曲线平滑效果图

4 结 语

由于传统PRM算法在产生采样点时使用的是均匀采样，导致了窄通道连通率不高的现象出现，文中采用了结合角点检测算法采样的PRM算法，最后采用Cardinal 样条曲线平滑路径。仿真结果显示，由于改进算法产生的采样点相对少而有效，故改进算法得到的路径可行、有效。