基于惩罚分位数回归的体脂率影响因素分析

李会贤， 袁晓惠， 周世权， 王 岳

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

体脂率是指人体内脂肪重量在人体总体重中所占的比例，又称体脂百分数[1]。体脂率是衡量人体健康程度的指标之一，通过对体脂率的研究，可以科学指导膳食营养，有效地控制体重和为医学观察提供客观依据。关于体脂率的研究有很多，例如张弛[2]通过测量部分大学生的身体成分指标，探讨了相关因素对体脂含量的影响。籍晓蕾[1]重点研究了城镇成年人体脂率与体重指数(BMI)和腰臀比(WHR)的关系，并且分析了影响体脂变化的相关因素。

分位数回归模型能够提供全面的回归信息以及关于响应变量条件分布的更多信息，最早由Koenker等[3]提出，其后应用于计量经济学、政治学、医学等多个领域。Koenker等[4]基于分位数回归探讨了1965-1985年影响世界主要国家经济增长的因素。Chen[5]应用分位数回归模型研究了美国8 250名男性的身体质量指数。李育安[6]介绍了分位数回归的概念、算法，并将分位数回归应用于经济领域的恩格尔系数上，说明了经济发展与收入增加对生活消费的影响程度，揭示了居民收入和食品支出之间的相关关系。谢兰云[7]利用分位数回归模型对我国R&D投入在不同分位点上影响因素的作用进行了详细研究。

当模型中协变量维数过高时，直接的估计方法效率很低，需要进行变量选择。较为流行的是通过加入惩罚函数来进行变量筛选。经典的惩罚是Tibshiani[8]提出的Lasso，该方法也成功应用到分位数回归模型中。Fan等[9]提出了SCAD惩罚，Zhang[10]构造了MCP的惩罚。Peng等[11]讨论了分位数回归下的变量选择，提出了迭代坐标下降(QICD)算法。

文中计划通过惩罚分位数回归模型来探讨体脂率影响因素，重点探讨各因素对体脂率的影响程度，以期达到控制体脂率，减少和预防因肥胖导致的疾病的目的。

1 惩罚分位数回归模型

分位数回归模型为

式中：yi----响应变量;

xi----k维自向量，xi=(1,x1,…,xk-1);

βτ----分别对应于x第τ分位数的回归系数;

ετ----随机分位数误差项,ετ=ε-q(τ);

q(τ)----误差的概率分布函数。

给定x时，响应变量y的第τ条件分位数为

Qτ(y|x)=xTβτ。

参数β的估计值表达式[12]

式中：ρτ----损失函数，ρτ=u(τ-I(u<0)),0<τ<1;

I(·)----示性函数。

当k很大且参数β存在0时，可以通过构建惩罚函数来提高估计效率。加入惩罚项后目标函数表达式为

式中：λ----调节参数,λ≥0;

pλ(|βj|)----针对β构建的惩罚函数项，j=1,2,…,k。

当惩罚函数pλ(β)=λβ时，此为Lasso惩罚。

Fan等[9]在变量选择方面展示了SCAD的Oracle性质。对于θ>0，惩罚项表达式为

pλ(|β|)=λ|β|I(0≤ |β|<λ)+

I(λ≤ |β|≤aλ)+

式中：a，λ----调节参数，此时为SCAD惩罚,a>2，λ>0。

对于a>1，惩罚项函数是

时，为MCP惩罚。

通过最小化惩罚函数，可筛选变量，提高估计效率。

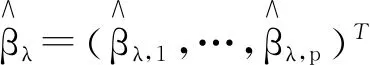
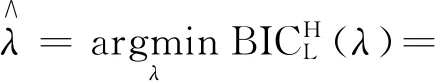
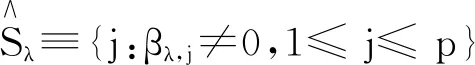
2 数值模拟

考虑分位数回归模型

其中，x=(1,x1,…,x6)，且x与误差ετ均服从标准正态分布，ετ=ε-q(τ)为随机分位数误差，q(τ)表示误差的概率分布函数。

给定样本量n=100，β的真值βZ=(1,1,2,0,0,0,0)，τ=0.5时，得到1 000个样本数据集，进行参数估计，并选取3种惩罚函数进行变量选择。

对于惩罚分位数回归模型，根据Fan等的建议，我们设定a=3.7来减少计算负担。列出了此模型是否加入惩罚的变量选择结果，见表1。

其中β0表示截距项的参数值，β1,β2,…,β6表示各回归系数值。

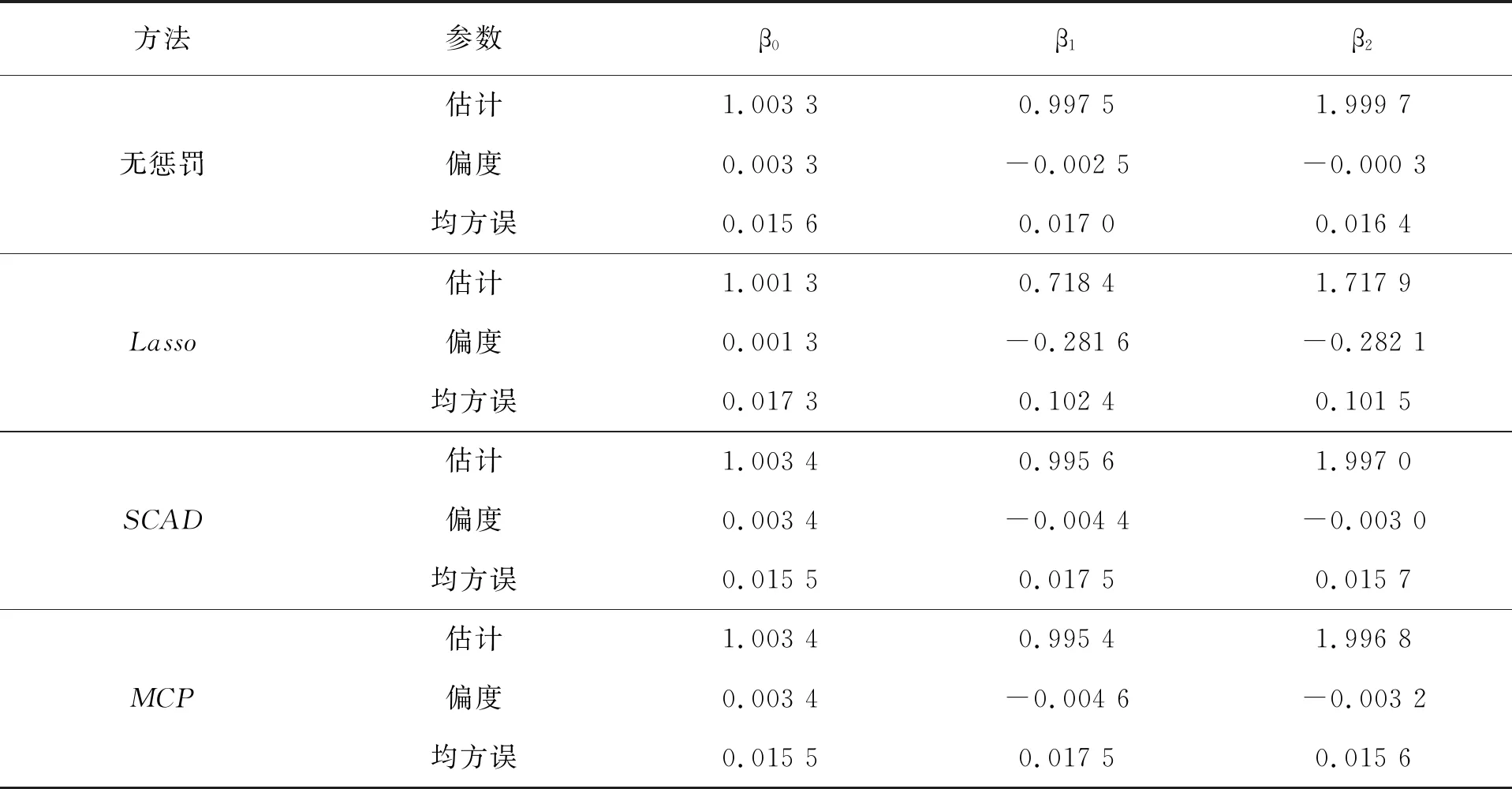
表1 不同方法的参数估计、偏度及均方误

注：由于在施加惩罚的模型中对真值为0的参数进行估计，并求得偏和均方误无意义，因此此表仅保留β0、β1、β2的估计结果。

在3种惩罚函数的变量选择中，SCAD和MCP惩罚运行效率相同，均方误最小，即估计效果最好。

给定样本量n=20、50、100时，令τ=0.3、0.5、0.7，生成100个数据集。列出了变量选择中参数估计的正确率与错误率,见表2。

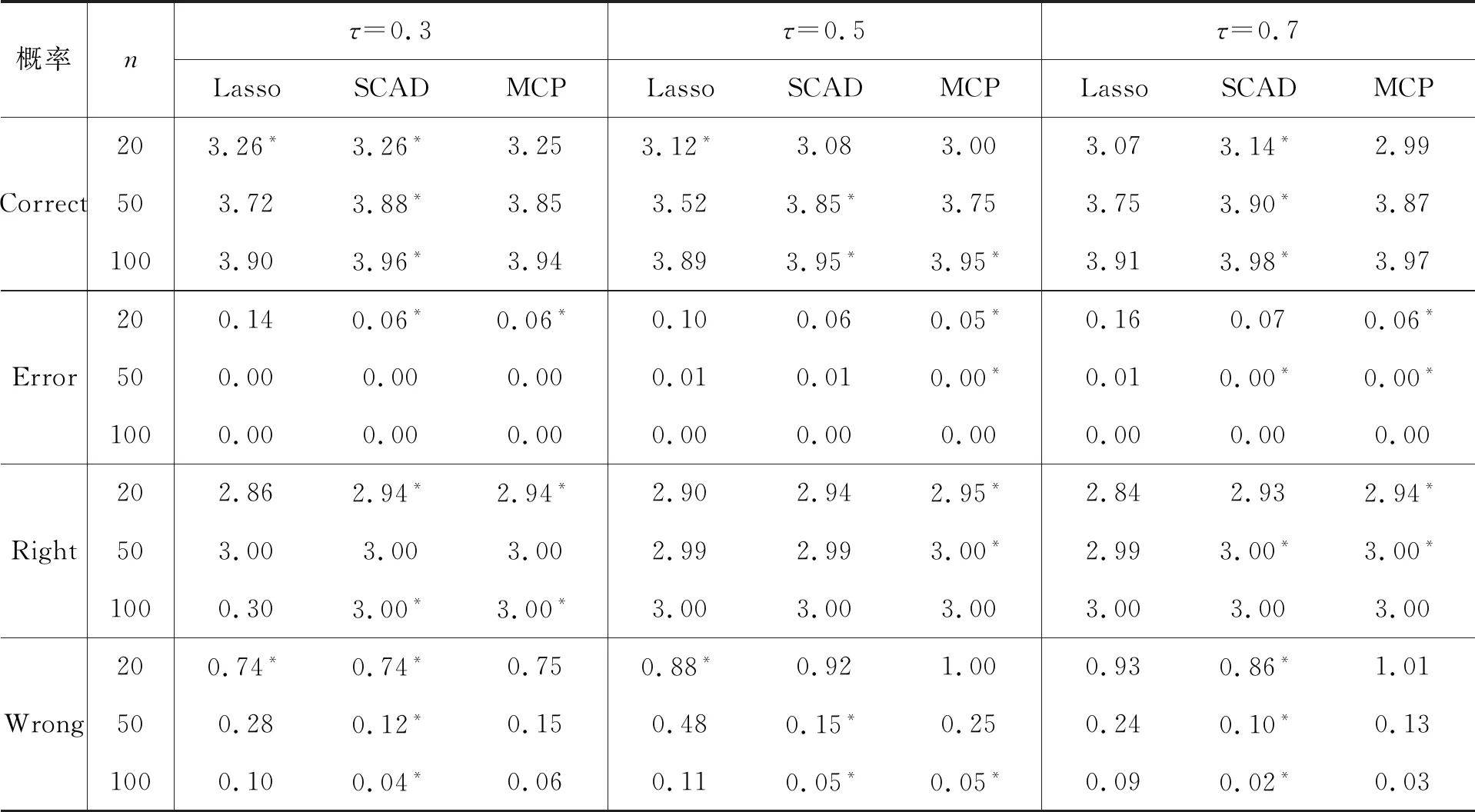
表2 τ不同时3种变量选择参数估计的正确率与错误率

注：“*”表示选择最好的概率;Correct表示真值为0，估计值仍为0的概率；Right表示真值非0，估计值非0的概率； Wrong表示真值为0，估计值非0的概率; Error表示真值非0，估计值为0的概率。

由表2可以看出,在不同的τ分位点处，均是SCAD变量选择的效果更好。

通过模拟实验发现：

1)分位数回归模型加入惩罚后，估计效率均有不同程度的提高，SCAD惩罚得到的估计效果最好。

2)比较变量选择的参数估计正确率，SCAD惩罚所得结果更精确。

分位数回归模型及其变量选择以往已经有许多人研究过，文中将此理论应用到对体脂率影响因素的进一步研究中。

3 实例分析

选择美国2003—2004年NHANES共6 596名被测试人群的体脂率数据[14]。由于体脂率(Totalpf)受到多种因素的影响，所以因素的选择至关重要。张弛[2]的研究提出：青春期开始以后，雄性和雌性激素分别有不同的作用，使男女体脂率出现差别，因此性别是影响体脂率的因素之一。区分性别的同时，年龄增长会导致人的体重和身高发生改变。体重发生变化，人体的各部分身体成分也在发生变化，从而影响体脂率。体脂率超标可能会导致高血压等疾病，所以也将秒内血压时间作为分析体脂率的一个因素。环境同样是影响体脂率的重要因素，但由于环境数据的复杂性和收集的困难性，因此将年收入水平作为环境因素的代表量。

综上所述，文中选定的影响因素为：性别(Gender，男性=1，女性=2)、年龄(Age)、年收入水平(aHI) 、秒内血压时间(BPTS)、体重(weight/kg)及身高(height/cm)。

采用的分位数回归模型是：

Totalpf=β0+β1τGender+β2τAge+β3τaHI+

β4τBTS+β5τweight+β6τheight。

τ不同时的参数估计结果见表3。

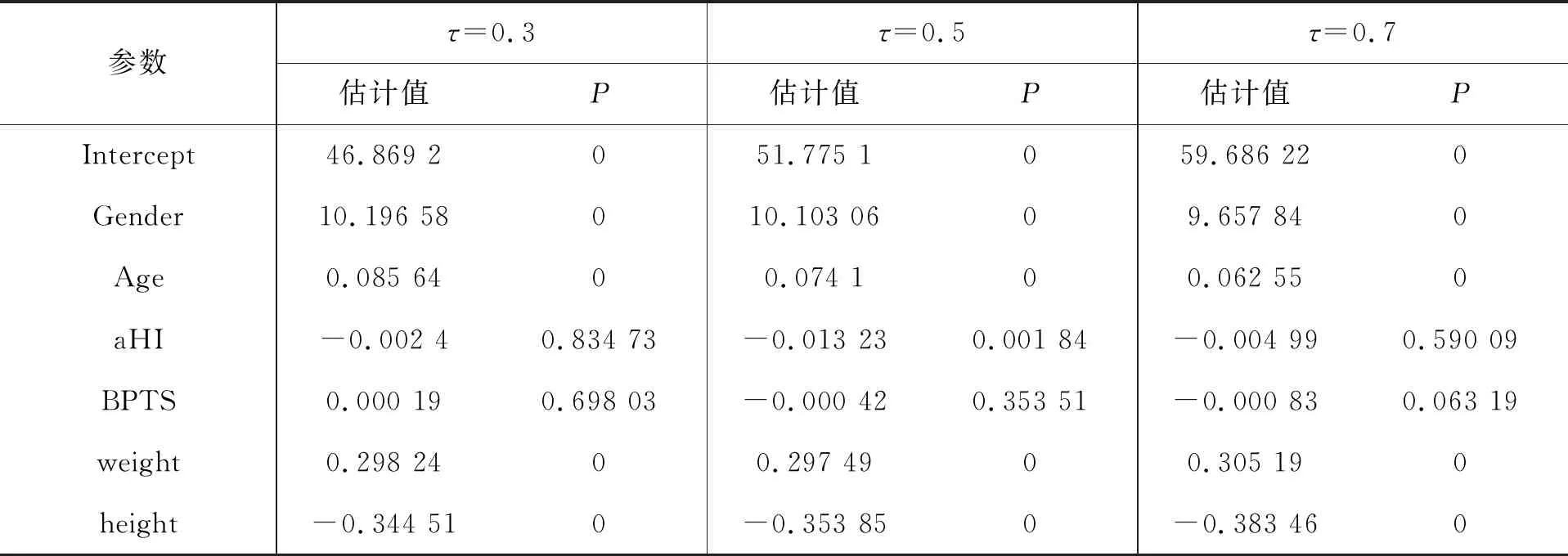
表3 τ不同时的参数估计结果及P值

体脂率的分位数回归模型在不同的τ分位点时，秒内血压时间对应的P值大于0.05，接受原假设，即参数不显著，年收入水平对体脂率的影响同样可以忽略不计，而性别、体重与身高的影响较大，身高是对体脂率呈负影响。

此模型系数在τ=0.1,0.3,0.5,0.7,0.9时的估计值分别如图1～图6所示。

通过图1和图2可以得出，性别和年龄在不同τ分位点对体脂率都是正影响，且体脂率水平较低的人群中受到性别、年龄的影响程度较大，而体脂率较高人群受两因素的影响程度会低很多。

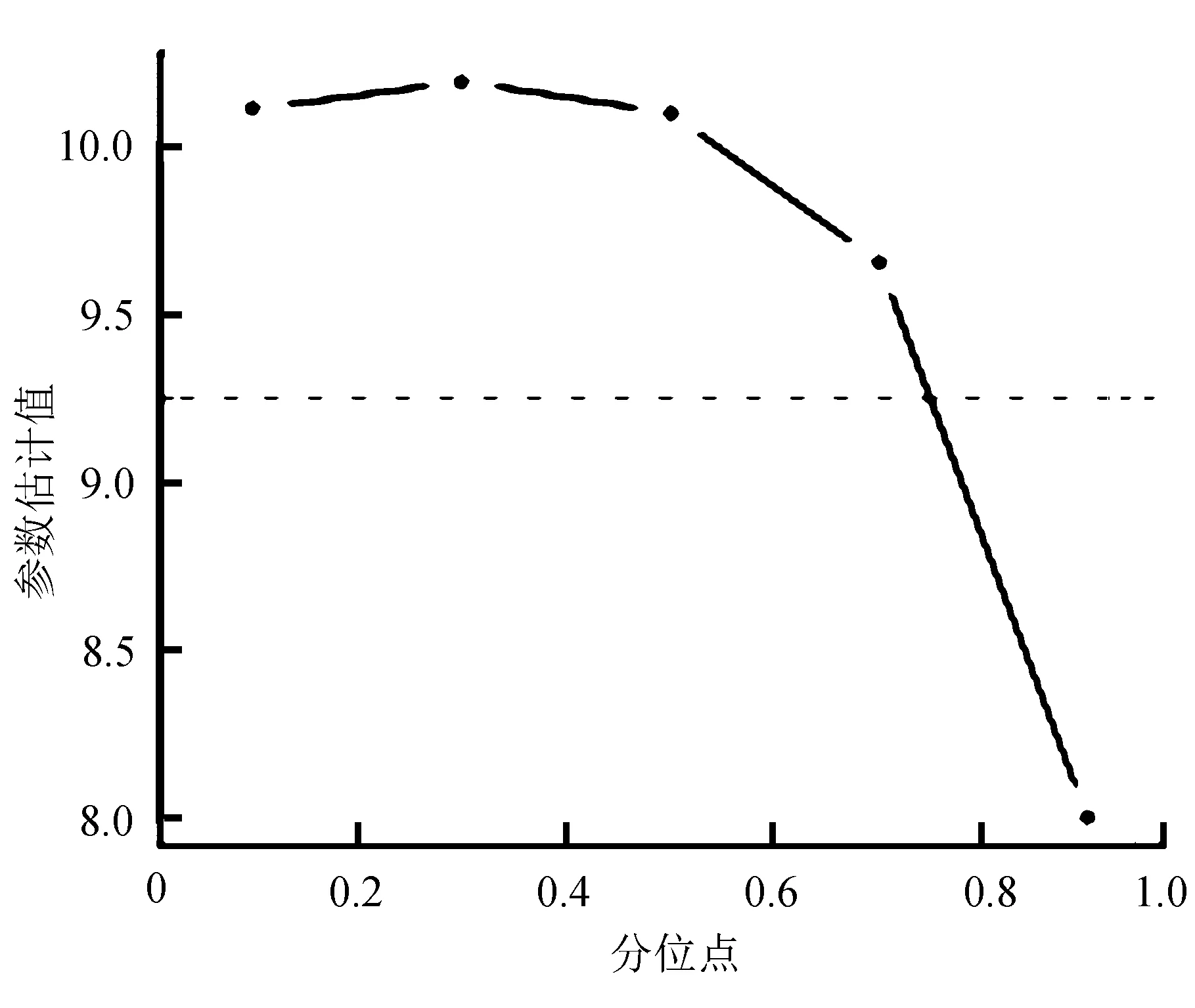
图1 Gender在τ不同时的参数估计值

图2 Age在τ不同时的参数估计值

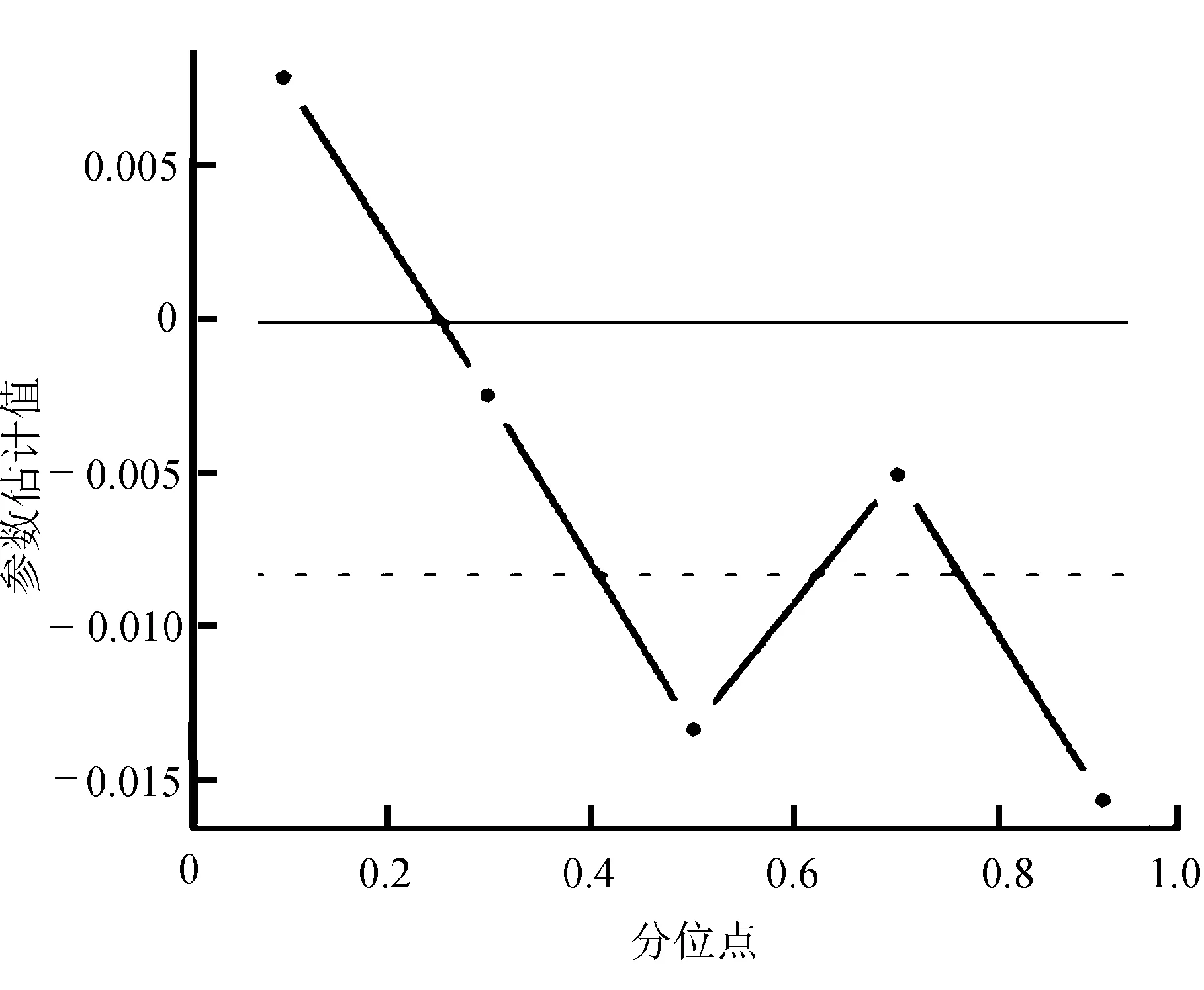
图3 aHI在τ不同时的参数估计值

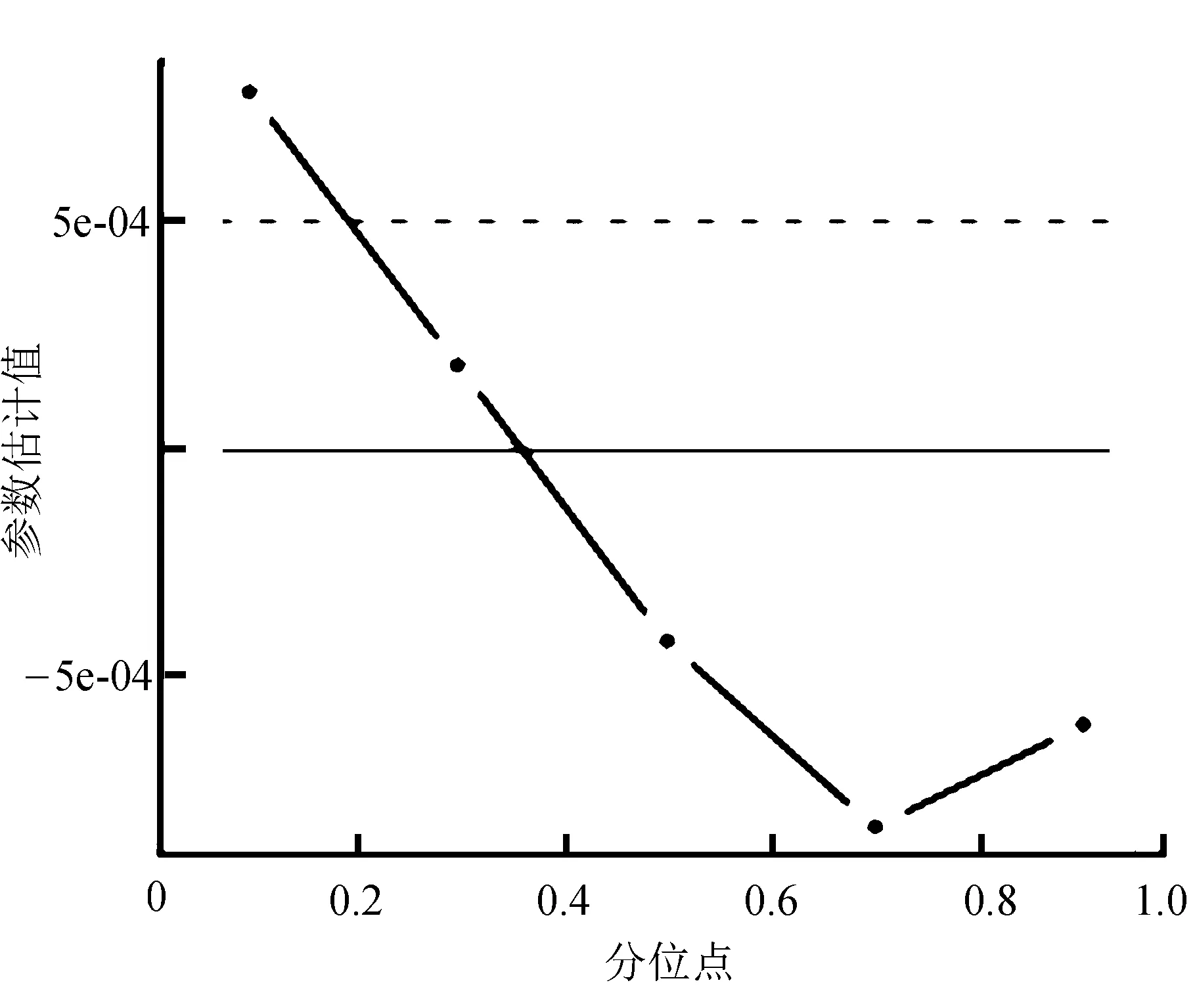
图4 BPTS在τ不同时的参数估计值

通过图3和图4可以得出，年收入水平和秒内血压时间对体脂率的影响是最小的，几乎可以忽略不计。

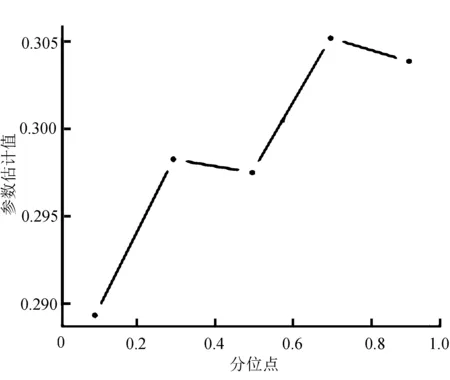
图5 weight在τ不同时的参数估计值

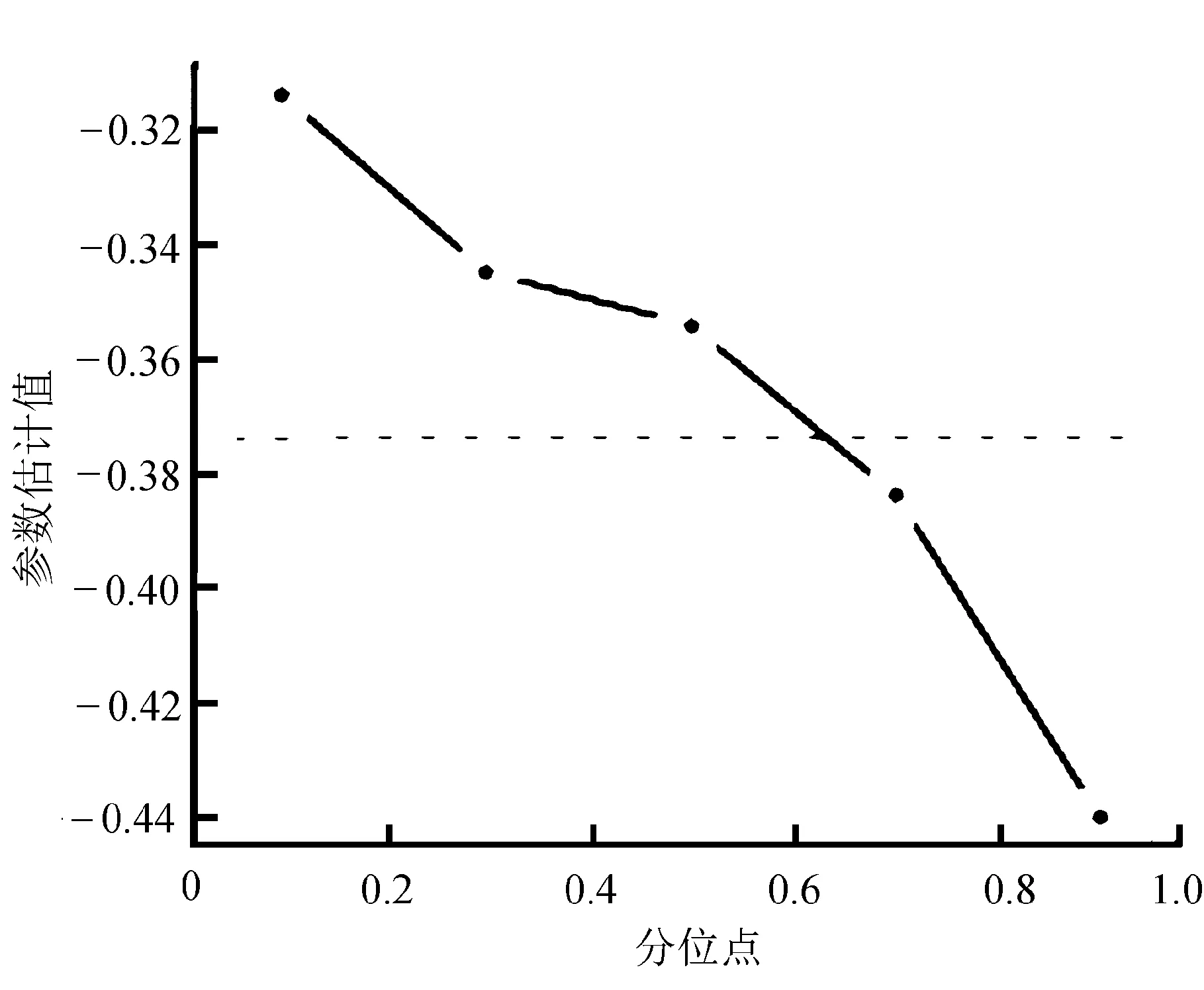
图6 height在τ不同时的参数估计值

通过图5和图6可以得出，体重系数在不同分位点处均为正影响，体脂率偏高的人群受体重因素的影响程度会较大，这也是人们的一个普遍认知，而身高对体脂率呈负影响，体脂率偏低的人群受到身高的影响更小。

体脂率数据在不同分位点进行变量选择时各参数估计结果见表4。

不同分位点下，Lasso、SCAD和MCP三种变量选择方法下，年收入水平对应的参数均为0，即年收入水平对体脂率没有影响，性别、年龄、体重与体脂率均呈正相关，而身高呈负相关。τ=0.5和τ=0.9较τ=0.1时，同样筛选出性别系数的参数为0，即对体脂率没有影响。偏瘦和偏胖人群中，秒内血压时间和身高与体脂率呈负相关；中等体脂率的人群中，秒内血压时间对体脂率是正影响，体重对体脂率的影响最大。

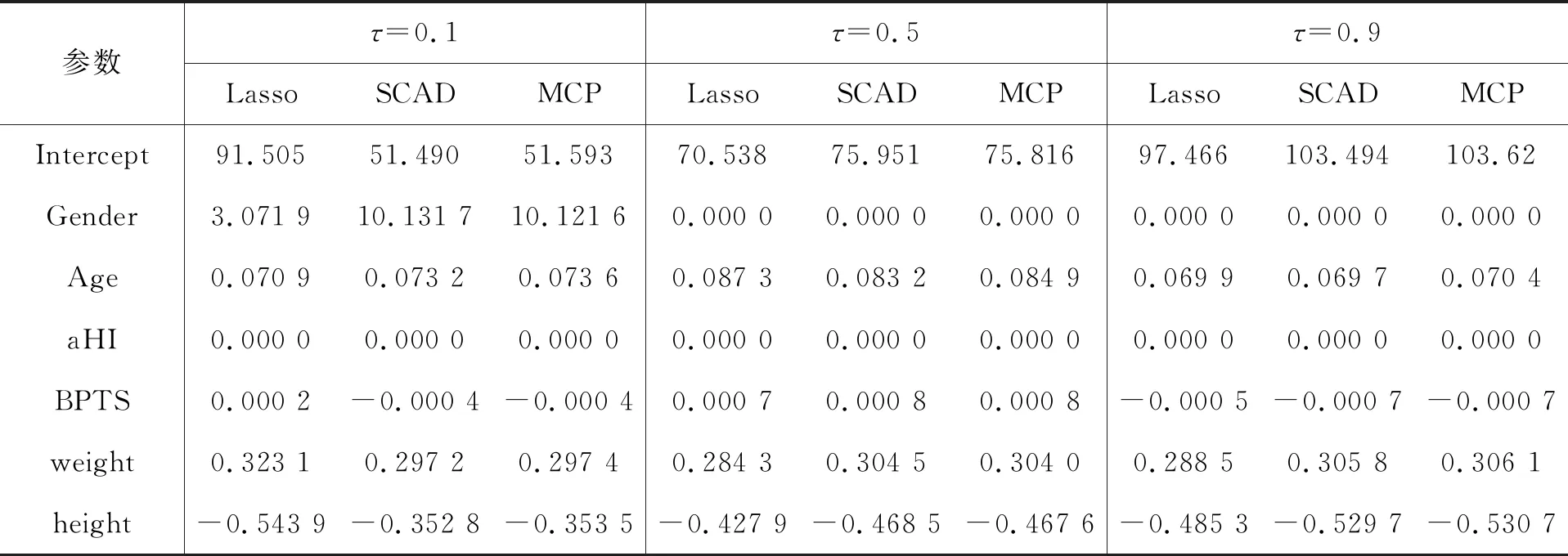
表4 Lasso、SCAD、MCP变量选择分位数回归模型的参数估计结果

通过实例研究发现：

1)体脂率的分位数回归模型中，秒内血压时间参数不显著，体脂率主要受到性别、体重与身高的影响。

2)变量选择过程中，年收入水平与秒内血压时间变量对体脂率几乎没有影响，得到与参数估计过程同样的结论。

4 结 语

由模拟实验和实例研究发现：通过惩罚分位数回归模型的数值模拟，SCAD惩罚得到的结果更精确，即估计效率较高;体脂率的分位数回归模型中，除年收入水平和秒内血压时间外其他参数均显著;性别、年龄、体重与身高对体脂率有较大影响，体脂率较高人群主要受到年龄和体重的影响。

如果想要保持体脂率达到适中水平并且维持健康，建议保持正常的体重，多锻炼身体，合理饮食。