角动量守恒定律的应用

李小芳, 王志梅

(1.中北大学信息商务学院， 山西 晋中 030600;2.太原师范学院 物理系， 山西 晋中 030619)

0 引 言

角动量守恒定律是物理学的基本守恒定律之一，大到宇宙天体，小到原子内部都服从这一定律，它在生产、生活、工程技术等方面有着广泛的应用。

1 角动量守恒定律

角动量定理的微分式为

对一固定点O或转轴,当物体不受力矩或所受的合外力矩M=0时，物体的角动量L保持不变，这个结论就叫角动量守恒定律[1]。

对于质点，角动量守恒定律的表达式为

L=r×mv=常矢量,

对于刚体，角动量守恒定律的表达式为[1]

L=Jω=常矢量。

2 角动量守恒定律在天体运动方面的应用

2.1 证明开普勒第二定律

开普勒行星运动第二定律，也称面积定律，指的是对任一行星，太阳和该行星的连线(矢径)在相等时间内扫过的面积相等。现用角动量守恒定律证明。

行星对太阳角动量的大小为

L=rmvsinθ,

(1)

式中：m----行星的质量;

θ----矢径r与速度v之间的夹角，行星速率

则

(2)

式(2)中

rsinθds=r⊥ds=2dA,

(3)

其中，dA为行星矢径在dt时间内扫过的面积，因此

(4)

由于太阳和行星之间的万有引力为有心力，它对力心的力矩为零，故行星的角动量守恒，即L=常量，因此

从而证明了行星的矢径在相同时间内扫过的面积相同。事实上，开普勒第二定律与角动量守恒定律等价。

2.2 证明太阳在焦点位置

开普勒第一定律：每一行星沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点上。现用角动量守恒定律及牛顿力学理论证明太阳处在椭圆的一个焦点上。

设椭圆方程为

式中：a----长轴;

b----短轴。

焦点位置为(0,±c)，且a2-c2=b2。

行星绕太阳运动时，行星所受的力矩为零，角动量守恒。由角动量守恒定律，得

r1mv1=r2mv2,

(5)

式中:v1,r1----分别为行星处于远日点时的速率及距太阳的距离;

v2,r2----分别为行星处于近日点时的速率及距太阳的距离。

由式(5)得

(6)

由于万有引力为保守力，只有保守力做功时，机械能守恒。由机械能守恒定律，得

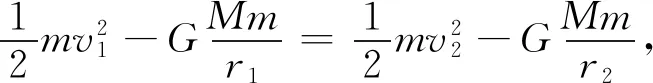
(7)

整理上式得

(8)

由向心力公式，得

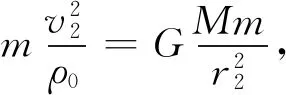
(9)

式(9)中长轴端点弧元的曲率半径

(10)

由式(6)、式(8)～式(10)得

r1r2=aρ0=b2，

(11)

又因为

r1+r2=2a,

(12)

联立式(11)和式(12)得

r2=a-c,

(13)

证明了太阳的位置为椭圆的焦点。

2.3 定性解释星系的扁平状旋转结构

对于很多星系来说，它们都是扁平状旋转结构。数学家拉普拉斯的“星云说”指出，星系旋转盘状结构的成因是角动量守恒。对于星系来说，其一开始是一个缓慢旋转的球状气体云，具有初始角动量。在垂直于轴向的径向上，星系由于引力作用慢慢向内收缩，因为引力为有心力，因此星系对转轴的角动量L=rmv守恒，当星系半径减小时，其速率增大，离心力也随之增大，当离心力增大至与引力恰好平衡时，星系停止收缩。对于轴向不存在离心力，则星系持续收缩，最终在引力的作用下，轴向变得非常扁平。因此星系形成了具有一定半径大小的扁平状旋转结构[2]。

图1 天体的旋转盘状结构

3 角动量守恒定律在工程技术方面的应用

3.1 进动陀螺仪

陀螺仪有两个特性：进动性和定轴性，这两种特性都是建立在角动量守恒的原则下[3]。

3.1.1 陀螺的进动

陀螺在绕自身对称轴高速转动的同时，其对称轴绕经过定点的竖直轴转动，这种高速自转物体的转轴在空间转动的现象叫做进动[4]。

陀螺的旋进如图2所示。

(a) 自转陀螺的对称轴同时绕OZ轴转动

(b) 陀螺的对称轴转动一定的角位移图2 陀螺的旋进

图2(a)中，质量均匀对称分布的陀螺在高速旋转时，相对于O点的角动量为

L=Jω，

(14)

式中：J----陀螺的转动惯量;

ω----自转角速度。

L的方向沿对称轴，由于陀螺质量对称分布，此角动量就是陀螺对自身对称轴的角动量。高速旋转的陀螺，在倾斜状态时，由于进动产生对O点的角动量远小于其本身对称轴的角动量，可将总角动量近似为对其自身对称轴的角动量。

以O点为参考点，只有重力产生力矩，重力的力矩

(15)

式中：dm----陀螺上小质元的质量;

r----质元相对于O点的位置矢量。

整理上式，得

(16)

式中：rC----质心相对于O点的位置矢量。

由于rC与L同向，因此重力对O点的力矩M始终与角动量L垂直。

在重力矩的作用下，dt时间内，陀螺自旋角动量的增量

dL=Mdt=mrC×gdt。

(17)

方向垂直于纸面向里，与L方向垂直。所以在重力矩的作用下，陀螺的自旋角动量大小不变，只改变方向，L的末端轨迹为圆。

图2(b)中，陀螺对称轴与竖直轴之间的夹角为θ，dt时间内，陀螺对称轴转过的角位移为dφ，自旋角动量的增量大小

|dL|=Lsinθdφ。

(18)

陀螺重力矩的大小

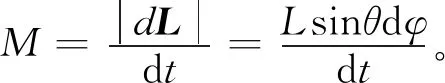
(19)

因此,陀螺的进动角速度为

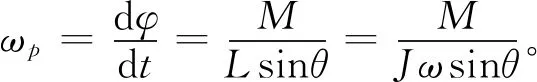
(20)

将式(16)代入式(20)，得

(21)

即进动角速度ωp与陀螺自转角速度成反比，与角度θ无关。ωp随自转角速度的增大而减小，自转角速度越大，陀螺越容易稳定旋转。当陀螺的自转角速度不够大时，则除了自转和进动外，陀螺的对称轴还会在铅垂面内上下摆动，称为章动[2]。

3.1.2 陀螺仪

陀螺仪如图3所示。

图3 陀螺仪

从图3可以看出，陀螺仪的转子、内环、外环都可以绕着各自的转动轴自由转动，三个转动轴正交于转子质心，在忽略摩擦和空气阻力的情况下，这种设计保证了转子所受的合外力矩为零，转子的角动量L=Jω守恒。陀螺仪的转动惯量J不随时间变化，若将陀螺仪的转轴指向某方向，当转子绕自身对称轴以角速度ω高速转动时，不管如何改变框架的方位，其中心轴的空间取向都始终保持不变，因而具有导航能力[5-6]。

高速转动的陀螺仪受到一定的干扰力矩后，转子的对称轴会在初始方位附近产生幅度很小的短时高频章动，保证对称轴的方向基本不变，因此具有极强的稳定性。但是如果陀螺仪持续受到干扰力矩的话，对称轴的指向会随时间产生误差。

我国的WS-35型155 mm口径制导炮弹，其最大射程可达到100 km，且精确度高，使用“北斗”卫星导航系统进行GPS/惯性制导(INS)。惯性制导的核心部件为三轴陀螺仪，其抗干扰能力和自主性强，但是存在导航精度随时间不断降低的问题。利用GPS的长期稳定性与适中精度可以不断对INS加以校准，消除INS积累的误差[7]。

3.2 直升飞机螺旋桨

直升飞机一般都有两个螺旋桨。当直升机静止在地面时，受到重力及地面给它的支持力，两力产生的合外力矩为零，直升机的角动量守恒。飞机静止在地面时，初始角动量为零，当直升飞机的主螺旋桨旋转时，机身必然会朝着反方向旋转。为了阻止机身旋转，需要另一个螺旋桨来产生阻力矩，使其与主螺旋桨产生的力矩相抵消。大多数直升机通过在尾部安装一个螺旋桨来阻止机身转动，但也有直升机采用反向转动的双旋翼来阻止机身旋转，“共轴双桨”与“纵列式双桨”的直升机分别如图4和图5所示。

图4 俄罗斯制造的卡50直升机

图5 雪地降落的支努干飞机

4 角动量守恒定律在游戏和体育方面的应用

4.1 扔水瓶挑战

“扔水瓶挑战”是一个风靡于社交网站的游戏，向空中旋转扔出一个装有部分水的瓶子，瓶子在空中翻一个跟头后，可以平稳垂直地站立在桌面或地面上。下面分析一下“扔水瓶挑战”背后所蕴含的物理知识。

在忽略空气阻力的情况下，水瓶被扔出去之后，只受重力，且重力通过质心，因此系统所受的合外力矩为零，角动量L=Jω守恒。由于水具有流动性，当瓶子在空中旋转时，瓶内的水并不会随着瓶子旋转，而是沿着瓶子晃动，导致水的质量沿着瓶子重新分布，从而改变了系统的转动惯量。

文献[7]构建了一个简单的一维模型来研究在空中旋转的水瓶，导出了系统的质心和转动惯量

(22)

(23)

式中:hCM----系统质心的位置;

J----系统的转动惯量;

Jb、Jw----分别为瓶子和水的转动惯量;

mb----瓶子的质量;

mw----瓶中水的质量;

H----瓶子的高度;

h----瓶中水的高度。

水瓶在旋转过程中，水的高度h时刻变化，因此,系统的质心和转动惯量也随时变化。水在瓶中晃动的时候，由于水的质量沿着瓶子分散分布，导致系统的转动惯量增大[8-9]。

根据角动量守恒定律，当系统的转动惯量增大时，其旋转角速度会减小。因此水瓶在落地时角速度较小，可以平稳垂直地站立在桌面或地面上。若游戏中使用空瓶子或装满水的瓶子，则挑战很难成功。空瓶子或装满水的瓶子在转动过程中可看成刚体，其转动惯量不变，水瓶旋转时角速度就会保持不变，水瓶落地时旋转角速度大，导致挑战失败。

“扔水瓶挑战”成功的关键有两个：一是尽量减小落地的角速度；二是尽可能降低系统的重心，重心越低系统越稳定。挑战时，瓶中的水不能太少也不能太多。水太少，系统的重心虽低，但其转动惯量增大不明显；水太多，系统重心不仅高，而且水在瓶中晃动不明显，对改变转动惯量没有太大贡献。经过实验和分析[8-9]，当瓶中的水为1/3～1/4时，“扔水瓶挑战”最容易成功。

4.2 体育赛事

体育赛事中的许多运动，同样是通过改变运动员自身的质量分布来改变旋转时的角速度，从而使表演更具有观赏性。

跳水运动员、花样滑冰运动员经常会做一些旋转动作，这些运动员的旋转速度可以通过改变肢体动作来实现。在阻力可以忽略不计的情况下，不论运动员在地面上旋转还是空中旋转，所受的合外力矩都为零，因此角动量守恒。当运动员收拢双臂或腿时，其转动惯量减小，旋转速度增大；当运动员伸开双臂或腿时，其转动惯量增大，旋转速度减小。

5 结 语

角动量守恒定律在诸多领域都有体现，是一个非常重要的理论，除了文中介绍的应用外，生活中很多常见现象也蕴含着角动量守恒定律的知识，因此角动量守恒定律及其应用研究非常重要。