关于初中几何解题方法的几点思考

江苏省苏州高新区第五初级中学校 刘志昂

一、一般问题的解决方法

一般问题是指比较基础的几何问题，通常的解决方法是“读题、读图，适当标记加联想”。“读题”是指逐字逐句地读题，要读出已知条件和要解决的问题，读出关键词，读出已知条件和未知条件之间的联系等；“读图”是指每读到一个已知条件，都要在图形上找到它的位置；“适当标记”是指每一个已知条件都要在图上做出适当的标记，比如相等的线段，用条数相等的短线进行标记，相等的角用条数相等的短弧线进行标记等；“联想”是指每读出一个已知条件，都要联想到它可以得出什么结论，或者与已有其他已知条件一起，可以得出什么结论。

例1：如图1，在△ABC中，BP平 分 ∠ABC，CP平 分∠ACB，且PD∥AB，PE∥AC，BC＝5，求△PDE的周长。

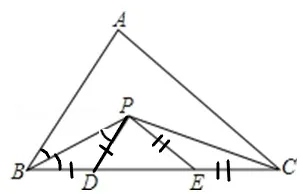
图1

分 析：“BP平 分∠ABC” 指 向 于“ ∠ABP= ∠PBD”，“PD∥AB”指向于“∠ABP=∠BPD”，两个条件在一起可以得到∠PBD=∠BPD，由“等角对等边”可以得到BD=PD，同理得CE=PE，这样△PDE的周长就转化为线段BC的长。

如上题所述，一些简单的几何问题运用此方法，可以直接得到解题的思路和方法。

二、复杂问题的解决方法

对于一些复杂的结合问题，运用上面的“读题、读图，适当标记加联想”不能马上解决问题，则需用“综合——分析法”，俗称“执果索因法”，即“缺谁证谁”。

例2：在△ABC中，AB＝AC，∠BAC＝90°。过点A作直线AP（如图2 所示），点C关于直线AP的对称点为点D，连接BD，CD，直线BD交直线AP于点E。

（1）依题意补全图；

（2）若直线AP旋转到如图2 所示的位置，请用等式表示线段EB、ED、BC之间的数量关系，并证明。

图2

图3

分析：（1）中的作图如图3，根据图形的轴对称性，可以得到AC=AD=AB，CE=CD，那么线段EB、ED、BC之间的数量关系就转化为线段EB、EC、BC之间的数量关系。三条线段之间的关系，常规的是和差关系（比如两条线段的和等于第三条线段）或者是两条线段的平方和等于第三条线段的平方。根据图形可以初步判断应该是后一种，那么解决问题的交点就集中在证明∠BEC是直角上，这就是初步的 “执果索因”。对于∠BEC是直角的证明，则从四边形ABEC的内角和入手，现在∠BAC是直角，则需证明∠ABE+∠ACE=180°，这是进一步的“执果索因”，由上面的AC=AD=AB，CE=CD可得∠ACE=∠ADB=∠ABD，而∠ABD与∠ABE互补，则∠ABE+∠ACE=180°，得到∠BEC＝90°，进而BE2+CE2＝BC2，故EB2+ED2＝BC2。

三、特殊问题的解决方法

1.线段和差关系的证明

线段之间的和差关系，是指几条线段的和或差与另外几条线段的和或差相等，对于这类问题的证明的常用方法是“截长补短”。如需要证明a+b=c，则可以将c截成两条线段，使其中的一条等于a，证明剩下的那条线段等于b，这叫“截长”；将线段a延长b的长度，得到一条新的线段d，则线段d的长度等于线段a与线段b的长度之和，只要证明d=c即可，这叫“补短”。

例3： 如 图4， 在△ABC中， ∠BAC＝75 °， ∠ACB＝35°，∠ABC的平分线BD交边AC于点D。

（1）求证：△BCD为等腰三角形；

（2）若∠BAC的平分线AE交边BC于点E，如图5，求证：BD+AD＝AB+BE。

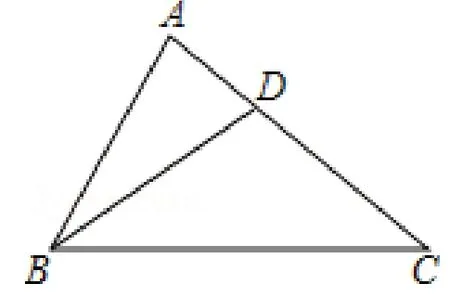
图4

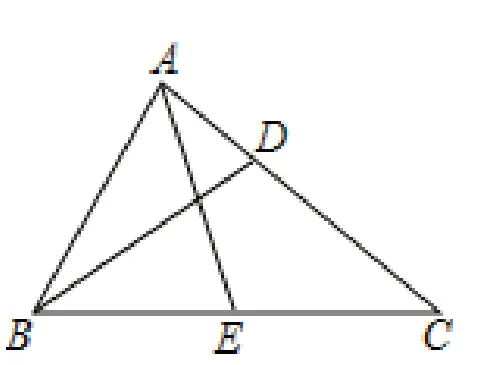
图5

分析：（1）如图4，先根据三角形内角和得∠ABC＝70°，由角平分线及已知角可得：∠DBC＝∠ACB＝35°，由此可得结论。

（2）证法一（截长）：如图5，在AC上截取AH＝AB，连接EH，证明△ABE≌△AHE，则BE＝EH，∠AHE＝∠ABE＝70°，所以EH＝HC，得AB+BE＝AH+HC＝AC＝BD＝CD。

证法二（补短）：如图5，在AB的延长线上取AF＝AC，连接EF，证明△AEF≌△AEC，则∠F＝∠C＝35°，得BF＝BE，由此可得结论。

2.几何解题中的分类讨论

几何解题中，由于一些特定的因素（如已知条件的不确定性、位置关系的不确定性等）的存在，导致了结论的不确定性，故需要根据不同的情况或者不同的前提对结果进行讨论，叫作分类讨论。分类讨论时需要注意：（1）分类时要按照一定的顺序，确保不重不漏；（2）讨论结束时，需要对问题给予总结性的结论。

例4：如图6，△ABC中，AC＝BC，∠ACB＝120°，点D在AB边上运动（D不与A、B重合），连接CD。作∠CDE＝30°，DE交AC于点E。

（1）当DE∥BC时，△ACD的形状按角分类是__________；

（2）在点D的运动过程中，△ECD的形状可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由。

分析：（1）由DE∥BC得到∠BCD＝∠CDE＝30°，再由∠ACB＝120°得到∠ACD＝120°-30°＝90°，则△ACD是直角三角形。

（2）对于△ECD是等腰三角形，分三种情况：EC＝DE、CD＝DE、EC＝CD。由于题目中是从角的角度来解决问题的，故还要转化为角的关系，分别对应为∠CDE＝∠ECD、∠ECD＝∠CED、∠CED＝∠CDE三种情况进行讨论，然后利用等腰三角形的性质和三角形内角和定理进行计算。

3.几何解题中的动点问题

在几何的有关计算与证明中，往往会遇到动点问题。一般是某一个或几个点沿着一定的方向，按照一定的速度运动。解决这类问题，往往是看清动点的起点和终点（可能会与自变量的取值范围有关），根据运动的速度、时间表示所有能表示出的线段的长，然后根据题中给出的相等关系或者是题中几何图形的性质得到相等关系，列出方程求解。

例5：在直角三角形ABC中，若AB＝16 厘米，AC＝12 厘米，BC＝20 厘米。 点P从点A开始以2 厘米/秒的速度沿A→B→C的方向移动，点Q从点C开始以1 厘米/秒的速度沿C→A→B的方向移动，如果点P、Q同时出发，用t（秒）表示移动时间，那么：

（1）如图7，请用含t的代数式表示：

①当点Q在AC上时，CQ＝__________；

②当点Q在AB上时，AQ＝__________；

③当点P在AB上时，BP＝__________；

④当点P在BC上时，BP＝__________。

（2）如图8，若点P在线段AB上运动，点Q在线段CA上运动，当QA＝AP时，试求出t的值。

（3）如图9，当P点到达C点时，P、Q两点都停止运动，当AQ＝BP时，试求出t的值。

分析：（1）根据三角形的边长、点的运动速度进行解答（这里就是上面所说的用动点运动的速度、时间表示所有能表示出的线段的长）。（2）根据QA＝AP这一相等关系列出方程，解方程即可。（3）根据分点P在线段AB上运动，点Q在线段CA上运动；点P在线段BC上运动，点Q在线段CA上运动；点P在线段BC上运动，点Q在线段AB上运动三种情况中，根据AQ＝BP这一相等关系列出方程，解之即可。

4.几何解题中的“模式识别”策略

在解决一些简单的问题或者简单的图形时得到了基本的结论，积累了基本的解题方法和解题思路，将之理解、记忆，遇到形同的、相近的、相关的、相似的问题时，可以用它来解决问题，简单地说，是“基本问题的基本结论，基本思路和基本方法”。

例6：探索与运用。

（1）基本图形：如图10，已知OC是∠AOB的角平分线，DE∥OB，分别交OA、OC于点D、E，求证：DE＝OD。

（2）在图11 中找出这样的基本图形，并利用（1）中的规律解决这个问题：已知△ABC中，两个内角∠ABC与∠ACB的平分线交于点O，过点O作DE∥BC，交AB、AC于点D、E，求证：DE＝BD+CE。

（3）若将图12 中两个内角的角平分线改为一个内角、一个外角（如图12，∠ABC、∠ACF）和两个都是外角（如图13，∠DBC、∠BCE）的角平分线，其他条件不变，则线段DE、BD、CE的数量关系分别是：图12：________________，图13：______________。

分析：（1）根据角平分线的定义得到∠AOC＝∠BOC，根据平行线的性质得到∠DEO＝∠BOC，等量代换得到∠DEO＝AOC，根据等腰三角形的判定即可得到结论。这里构造出一种“角平分线、平行线和等腰三角形”模式：在这种特定的图形结构之下，DE∥OB，OC平分∠AOB和DO=DE，三者可以知二得一（即知道任意两个结论，都可以推出第三个结论），也可以理解为：在特定的图形结构之下，角平分线、平行线和等腰三角形可以知二得一。（2）根据图形的结构特征，显然存在着两个上述的基本“模式”中的基本图形，根据上述“模式”中蕴含的结论和思路、方法，很快便可以得到BD=DO，OE=CE，然后利用等量代换即可解决问题。（3）图12 中，根据前面的“模式”，可以得到DB=DO，EO=EC，所以DE=OD-OE=DB-CE。图13 中，根据前面的“模式”，可以得到DB＝DO，EO＝EC，所以DE＝OD+OE=BD+CE，