初中数学深度学习的内涵及实践策略分析

江苏省徐州市第十中学 曹 芮

在新课程背景下，人们越来越关注于学生核心素养培养策略的合理性，为了让初中生能够保持更高涨的数学学习热情，教师就应当从学生原有学习经验入手，丰富教学手段而搭建认知平衡的深度学习课堂环境，提升初中生逻辑思维能力以及数学模型构建能力。接下来，笔者将从三个方面简单介绍如何在初中数学课堂上构建深度学习模式。

一、重视学习经验，构建深度学习课堂

教师在为初中生进行知识讲解的时候，学生必然会对课堂所讲解的知识产生疑问，但是教师讲解知识的方法学生无法迅速适应，所以，教师应当基于学生心理状态以及学习习惯等，经常性地组织同学之间学习经验交流活动。每个同学在学习数学知识的时候都会有所体会，而宝贵的学习经验值得其他同学甚至教师借鉴学习。学生之间沟通起来更加方便，他们往往能够用更容易被同龄人所接受和理解的方式进行数学知识介绍。学生应当用于与他人分享自己的学习感悟和经验，在学生、教师深度沟通交流当中，数学课堂氛围得到优化，学生自身成为氛围营造者，同时他们也是良好学习氛围的受益者。

深度学习能够帮助学生更好地梳理知识脉络，进而将看似没有太多干系的各章节数学知识整合在一起构建完善的知识框架，在今后数学学习当中，学生也会依照具体情况灵活运用各部分知识解决实际问题。例如，教师在为学生讲解“勾股定理”的时候，可能有的学生对于“勾三股四弦五”的口诀感到无法理解，为了令学生真正学会“勾股定理”，教师就可以要求学生相互之间进行“勾股定理”概念以及性质讲解，同学之间相互合作，将自己对于勾股定理的理解阐述给其他同学。每一个同学对于勾股定理的理解都有所不同，通过聆听他人学习经验和感悟，学生自身也会有一张豁然开朗的感觉，对知识理解更深。

二、引入数学模型，构建深度学习课堂

数学概念知识相对其他学科而言更加抽象、晦涩，教师为了让学生对各种数学概念、公式等有更进一步的认知，就应当重视对学生核心素养的培养，通过引入数学模型的方式将抽象数学知识转化为看得见、甚至摸得着的事物，这样能够激活学生学习兴趣，接着教师充分发挥自身引导者的作用，为其细致介绍各项定理、概念的推理证明过程，当学生对于推导过程有所了解以后，也能将证明推导过程牢牢记在心中，即使今后忘记了定理部分内容，也可以延顺推导过程现场完成定理填充。另外，学生脑海中也会逐渐形成将数学问题具象化数学模型的思维习惯，使解决实际问题能力得到增强。

比如，教师在介绍一次函数相关知识的时候，为了让学生真正在生活中能够构建一次函数解决实际问题，就首先锻炼学生对于一次函数数学模型的想象能力。例如，如果我们要往如图1 所示的容器中均匀注水，那么容器中水面高度数据应当怎样变化？

这样的一道与生活紧密相关的题目，其实就是一次函数最常见的应用情况，学生需要首先考虑：在一次函数图像之中，什么因素应当作为x,y轴？水面增长速率需要以什么形式表现出来？结合图像中容器形状，我让学生直接以高度、时间为x,y轴，结合生活经验中往容器注水，水面变化情况很轻松就会画出对应的一次函数图像。

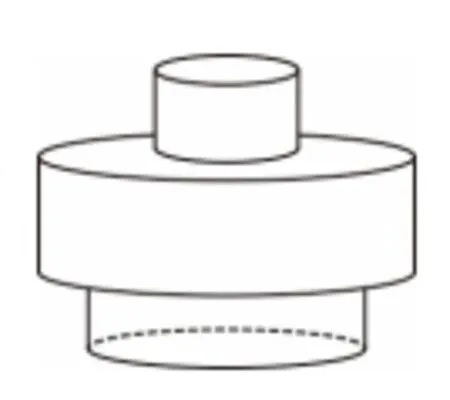
图1

三、评价学习过程，构建深度学习课堂

在传统数学教学过程当中，教师更重视学生究竟有没有掌握本节课重点知识，虽然这样的教学理念并没有错，但是却会在学生的脑海中留下“注重结果，不重视过程”的印象，但是数学学科的魅力正在于进行数学定理的证明过程，在这个推导过程当中学生的逻辑思维能力以及知识迁移能力得到充分锻炼。所以，教师应当以过程性评价作为深度学习课堂构建关键导向因素，强调数学知识学习、探究过程的重要意义，让学生能够以更积极的态度配合教师完成课堂教学任务，发自内心地希望深入研究过程，而教师再对初中生学习过程加以中肯评价，实现对学生过程指导，提升课堂教学效率。

例题：如图2 所示，在梯形ABCD中，AB∥CD，BD⊥AD，BC=CD，∠A=60°，CD=2cm。试求∠CBD的度数为多少，AB长度为多少。

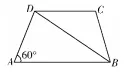
图2

教师为学生布置这样一道简单几何题，然后要求学生将求解过程清晰而完整地写出来。学生的思考过程一般都是首先从题目中给出的“AB∥CD”条件入手，得到∠A的补角∠ADC=120°，接着利用“BD⊥AD”得到∠CBD=∠CDB的关系，求得∠CBD=30°。而为了求得AB的长度，学生往往会将梯形分割为两个三角形，然后依照特殊直角三角形

三边长关系求出BC=CD=2cm，AB=2AD=4cm。本题目难度不是很大，所以教师在进行评价的时候更要侧重于对学生解题过程的评价，保证学生在解答题目时语言描述精简、求解过程一目了然。在长期评价模式影响下，学生逻辑思维能力以及语言表述能力均会得到明显提升，继而实现了全面发展。

总而言之，深度学习模式在近些年来越来越为人们所重视，初中数学教师应当不断提升专业素养，为学生提供更丰富合理的深度学习策略，并给予学生充分自主探究的机会，另其将数学知识真正地转变为解决问题的工具，提升综合素养，为今后学习打下扎实的基础。