改进混合蛙跳算法的研究
高建瓴,潘成成,吴建华,陈娅先,王 许
(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)
蛙跳算法(Shuffled Frog Leading Algorithm)是一种启发式算法,通过启发式函数进行启发式搜索,从而找到组合最优问题的解。混合蛙跳算法的运行原理从仿生上来说可以这么认为[1]:在一个池塘,有若干块石头,青蛙可以落在石头上,每块石头上可以获取到的食物数量是不同的,在池塘中有很多只青蛙,也有很多块石头,青蛙间可以交流,这样所有青蛙就都会往自己所在蛙群中所知道的最多食物的方向跳,或往全部青蛙中食物最多的方向跳,最终在池塘中找到最多食物的石头。他结合了以遗传为基础的memetic算法和以社会行为为基础的粒子群优化算法的优点[2],其显著特点是具有局部搜索与全局信息混合的协同搜索策略,寻优能力强,易于编程实现。
虽然混合蛙跳算法具有概念简单,调整的参数少,全局搜索寻优能力强,易于实现的特点。但是该算法与其他群智能优化算法类似也存在着一些缺点,求解精度不高、收敛速度慢、算法易陷入局部最优的问题。针对这些问题,近年来也有不少的国内外学者对其进行研究改进,张新明等[3]提出了将每次只更新组内最差青蛙的方式改为更新组内所有青蛙的方式,增大了获得优质解的概率,提高可操作性和优化效率。赵红星等[4]提出了对青蛙的觅食机制和更新迭代公式重新定义,青蛙的第一步向组内其它蛙搜索,第二步向组内最优蛙搜索,第三步向全局最优蛙搜索,提高混合蛙跳算法的全局和局部搜索能力。戴月明等[5]提出一种新的协同进化混合蛙跳算法,在局部搜索中对最差蛙的更新引入平均值,扩大青蛙搜索空间;在全局搜索中采取精英群自学进化机制,对精英空间进行精细搜索,提升全局搜索能力。李敏楠等[6]提出通过引入自适应同步因子,改变局部搜索蛙跳规则,从而增加种群的多样性。周林锦[7]提出对初始种群引入Tent混沌来改进,在最差个体更新中引入扰动的柯西因子,提高算法的寻有能力。虽然以上文献在一定程度上提升了算法的优化能力,但随着更多复杂优化问题和严格实时性要求的提出,需要求解精度更高、优化性能更好的混合蛙跳算法,因此,对于混合蛙跳算法的改进仍然有较大空间。本文在传统算法的基础上,通过引入自适应同步算子和惯性权重系数,提出一种新的混合蛙跳算法,改变个体青蛙更新公式,提高算法的求解精度、收敛速度、避免陷入局部最优。
1 标准混合蛙跳算法
在混合蛙跳算法中,种群被分为若干个子群(memeplex),每一个子群包括一定数量的青蛙。不同的子群具有不同的文化,分别进行局部搜索。在每个子群中,每只青蛙都有自己的想法,并且受到其他青蛙想法的影响,通过文化进化来发展。这样经过一定的文化进化以及跳跃过程,这些想法思路就在各个子群中传播开来,然后局部搜索和跳跃,直到收敛或满足标准为止。

(1)
式中:Di表示该子群中适应度最差解xw的第i次更新步长,Dmax是青蛙移动的最大步长,其中rand()为0-1之间的随机数。通过对最差解xw的更新得到新解xnew,即跟新最差青蛙的位置,如果新解的适应度值优于原来的最差解,就用xnew代替xw,否则,就用全局最优解xg替代式(1)中的局部最优解xb得到新的更新式(2),对最差解进行更新。
(2)
如果新位置xnew优于原来的解xw,就用xnew替代xw,否则,随机生成一个新解xnew代替xw;不断循环以上操作,直到满足局部迭代次数,再对下一组子群进行更新。对所有子群都完成局部搜索后,将全部的青蛙个体重新混合、排序和分组,进行下一轮的局部搜索,直到满足全局混合迭代次数G,进化结束,输出全局最优值[10]。
2 改进的混合蛙跳算法
2.1 自适应同步因子
在混合蛙跳算法中种群进行局部搜索是算法寻优的核心步骤,在局部搜索过程中,青蛙移动距离的大小对于算法的运算速度和搜索精度十分重要[11]。步长较小有利于精细搜索,但寻优速度比较慢且容易陷入局部最优值;步长较大可使青蛙容易在全局范围内展开搜索,提高搜索速度,但同时容易在搜索过程中跳过全局最优解所在位置。在标准混合蛙跳算法中,最差解的移动步长是随机更新的,这种随机的跳跃距离使最优解的引导作用无法充分发挥,容易使算法陷入局部极值或跳过全局极值[12]。因此,本文在算法局部搜索时,引入了动态自适应同步因子;当自适应移动因子为增函数时,在更新初始阶段移动距离比较小,对周围进行精细搜索,保持种群的多样性,在更新迭代中后期,移动步长增大,保持算法的全局搜索能力,避免算法陷入局部极值。
在标准混合蛙跳算法更新公式中的移动因子为rand(),是0~1之间的随机数,所以采用余弦函数为模型,设计了动态自适应移动因子如下:
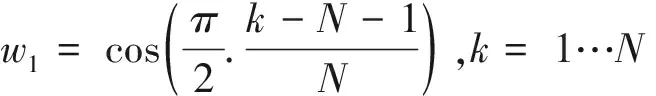
(3)
其中N表示子种群中最大进化代数,k表示子种群内当前进化代数,用自适应移动因子w1替代标准蛙跳算法更新公式中的rand()。w1在[-π/2,0]范围内逐渐递增,且在青蛙搜索接近结束时,保持平缓的变化率,有助于算法在搜索完成时速度以较小的变化率平稳进行搜索。
2.2 惯性权重系数
为了拓展搜索空间,提高算法的寻优能力以及收敛速度,在标准混合蛙跳算法局部搜索的基础上,引入上一次的移动步长的惯性权重系数,表示对过去经验的记忆[13],调节青蛙移动步长,在扩大青蛙的搜索区域的同时也加快了收敛速度,具体的惯性权重系数如式(4)所示:
ω2=(ωmax-ωmin)k/N
(4)
其中wmax和wmin是权重系数的最大值和最小值,k为子群当前进化次数,N为子群最大迭代数。如果w2较大,则算法全局搜索能力较好,反之,如果w2较小,则有利于算法局部搜索能力,因此w2的大小至关重要。经过实验表明,本文的wmax和wmin分别取值0.9和0.4。如果上一次的移动距离比较理想就保留,反之,就消除历史不良影响,去掉上一次的移动距离,使收敛速度加快。且惯性权重系数在初始阶段变化率大,有助于提升算法局部搜索的效率;在中后期阶段惯性权重系数变化率小,使算法进行精细的搜索,利于找到最优解。
2.3 改进混合蛙跳算法流程
本文改进混合蛙跳算法流程如下:
Step1:随机初始化青蛙种群和移动步长。在可行解空间生成F个维度为S的青蛙{x1,x2,…,xF},随机初始化移动距离Di′,Di′∈[-Dmin,Dmax]。
Step2:划分子群。计算每一个解的适应度值,将其降序排列,并将排序后的最优适应度的解记为xg。按照规则划分子群,标记群内最优可行解xb和最差可行解xw。
Step3:局部搜索。按式(5)对子群内的xw进行更新:
(5)
如果产生的新解优于旧解,就用新解替换子种群中最差解;否则,就用式(6)对最差解进行迭代更新,式中不包括上一次的移动步长,因为根据式(5)更新后的解没有忧于原解,说明上一次的移动距离不够理想,所以要去除历史不好影响,加快收敛速度,使青蛙迅速移到最优解附近。
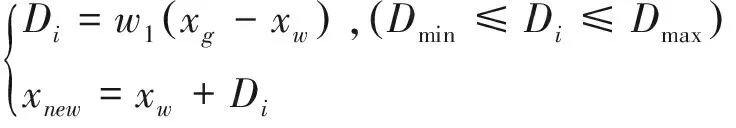
(6)
如果新解优于旧解,就用产生新的解替换子种群中最差解,否则,随机产生一个新解替换原来最差解,并随机生成Di',Di'∈[-Dmax,Dmax]。
Step4:当所有子种群更新完成后,对所有子种群的青蛙重新进行混合,形成新的族群,返回Step2,直到达到设定的全局最大迭代次数,算法终止,输出最后的全局最优解 。如图1所示,为改进蛙跳算法的程序流程图。
3 实验结果与分析
3.1 实验设置
为了验证改进混合蛙跳算法(ISFLA)的收敛性能,本文选用6个15维的测试函数进行实验分析,并与标准混合蛙跳算法(SFLA)进行对比实验。各函数的表达式、搜索范围以及理论最优值如表1所示[14]。表中f1(x)和f2(x)为单峰函数,通常用来考察算法的收敛速度,f3(x) 到f6(x)这四个测试函数为复杂多峰函数,可以检验算法的搜索性能,六个测试函数的理想最优值都为0。

图1 程序流程图Fig.1 Program flow char
本文为了提高实验的可比较性,设置相同的实验参数,具体如下:种群青蛙总数为F=400,子群数目为m=20,子种群中青蛙数目为n=20,局部更新迭代数目为N=30,全局更新迭代次数为G=300,最大移动步长为Dmax=1。软件使用Matlab,操作系统为Windows10,硬件配置CPU为4 G,硬盘容量1000 G。
3.2 结果分析
为了使实验结果更加客观准确,使算法单独运行30次,取30次实验结果的最好值、最差值、平均值作为参照指标进行对比分析[15],如表2所示。同时为了可以直观的看出两种算法的寻优能力,给出如图2所示各测试函数的进化曲线图。

表1 测试函数Tab.1 Test function
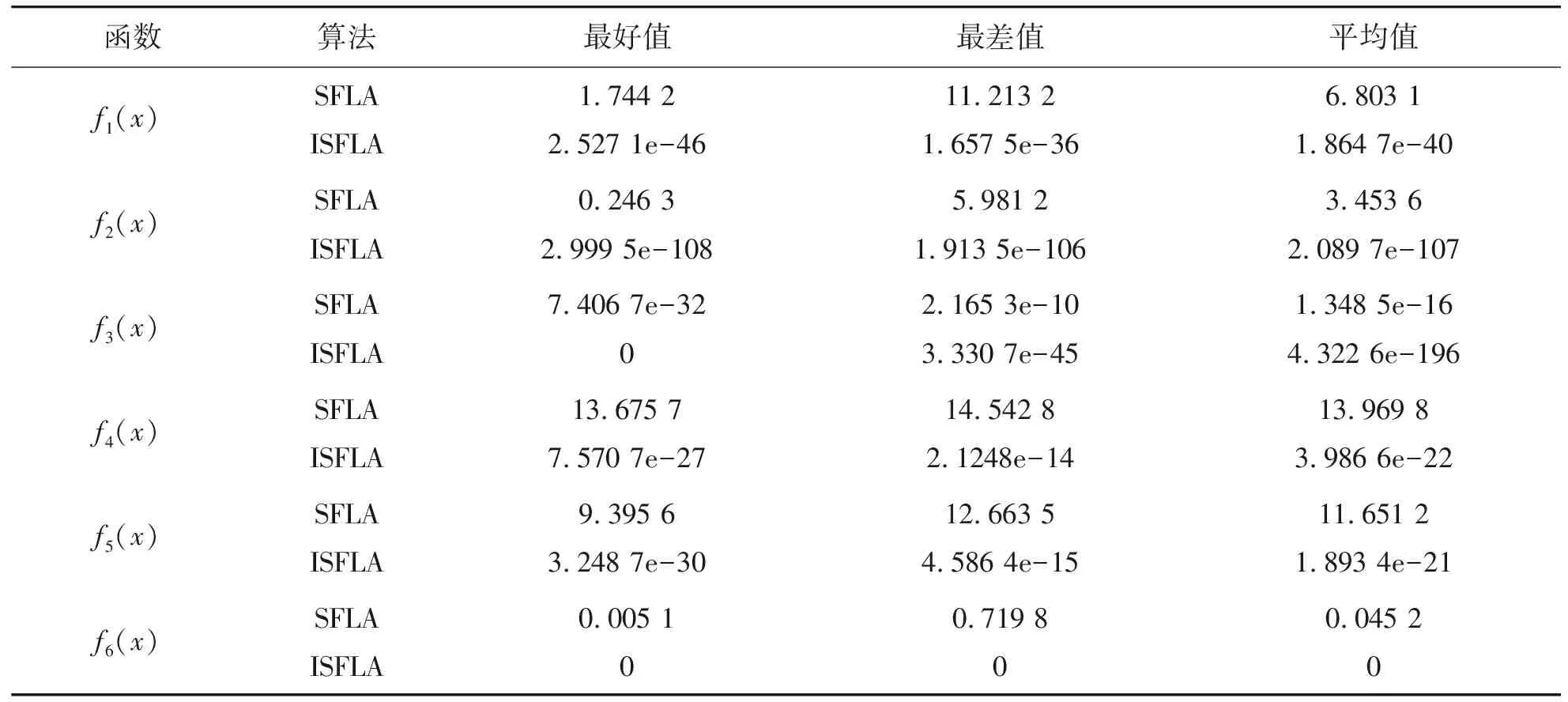
表2 测试函数的寻优结果Tab.2 Optimization results of test functions
通过表2可以看出,在相同的设置参数下,本文算法在最差值、最好值、平均值都优于标准混合蛙跳算法;在表2中,最好值是运行算法30次结果中最优的一次,最差值为运行算法30次中结果最差的一次,平均值则是对30次结果求平均,表1中的6个测试函数的最优值为0,ISFLA在六个测试函数中无论是最好值、最差值还是平均值都比SFLA更接近理想值0;且在f3(x)函数运行的30次结果中最好值达到了函数的最优值,在f6(x)函数的运行结果中每次均能收敛到最优解,而SFLA在各个测试函数中都出现了早熟收敛,在6个测试函数中30次运行结果没有一次是收敛到最优值0,通过表2的对比,可以明显看出ISFLA比SFLA的收敛精度高,寻优效果好。图2 是SFLA和ISFLA在6个测试函数中的进化曲线图,纵坐标表示函数最优解,横坐标表示种群的总进化代数,从图2中可以很直观的发现,ISFLA在f1(x)到f5(x)五个测试函数中进化曲线一开始就体现出比SFLA跟优秀的寻优能力,寻优值都几乎接近函数最优值0,并且收敛速度快,在f6(x)函数中虽然ISFLA刚开始的寻优精度没有SFLA好,但是当进化到50代左右时,ISFLA的寻优精度变得比SFLA好并且迅速找到最优解,SFLA则在各个测试函数中都出现了不同程度的早熟收敛,因此本文改进的混合蛙跳算法在求解精度、收敛速度上比标准混合蛙跳算法有了大幅度的提高。这是因为在传统蛙跳算法中加入自适应移动因子和惯性权重系数之后,保持了种群的多样性,扩大搜索范围,提升算法搜索效率以及搜索能力,说明本文对传统混合蛙跳算法的改进是有效的。
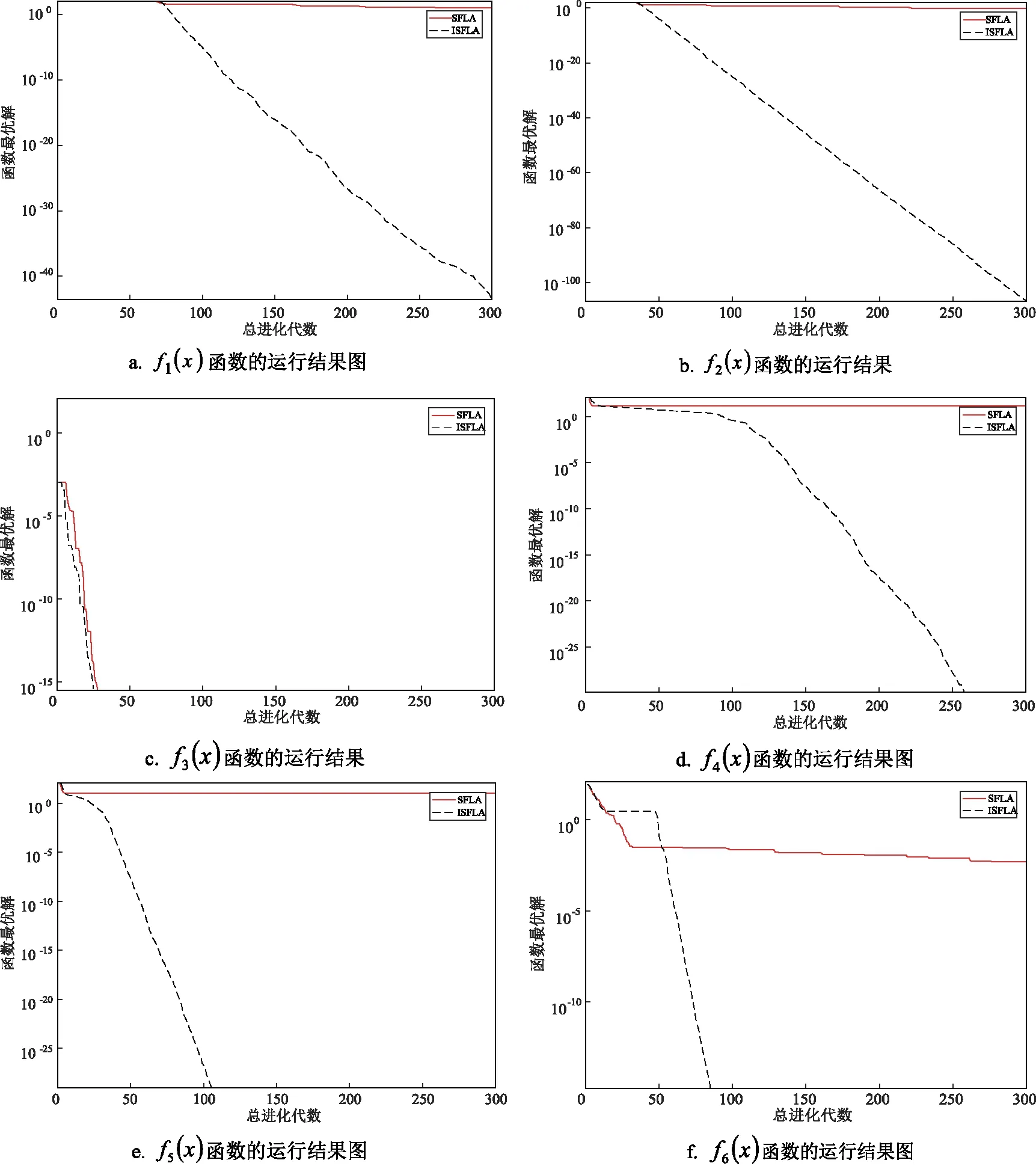
图2 各测试函数的优化对比结果图Fig.2 Optimization comparison results of each test function
4 结论
本文提出的一种基于自适应移动因子、惯性权重系数的混合蛙跳算法,有效地改善算法在优化过程中出现的求解精度不高、收敛速度慢、易陷入局部最优等缺陷。在局部搜索过程中改变蛙跳策略,扩大算法的局部搜索范围,保持种群多样性,通过6个15维测试函数的实验对比分析,表明本文改进的算法较传统混合蛙跳算法寻优精度更高,算法寻优性能更好。

