基于SV模型的行程时间预测
杨 超,胡 尧,2*,商明菊,李 扬,周江娥
(1.贵州大学 数学与统计学院,贵州 贵阳 550025;2.贵州省公共大数据重点实验室,贵州 贵阳 550025)
行程时间是交通规划、运营和能力评估的重要指标。为了实现对车辆进行实时管控和疏导,行程时间必须进行实时预测,且要有较高精度。由于受到车流量与行人随机性变化及道路其它不可控因素的影响,导致出行者行程时间的变化具有时变、无规律和随机的特性,且呈现出较为复杂的波动特征。
目前,在道路行程时间短时预测研究中,国内外学者也提出了较多可靠的分析方法,主要包括随机漫步法、线性回归、神经网络、时间序列、模糊逻辑模型和支持向量机等[1]。随机波动率(Stochastic Volatility,SV)模型在1986年被提出以来,人们在对金融数据的处理上建立了大量的模型来拟合分析数据,从而做出合理的预测和估计,其中SV模型就是大量被采用的一种金融模型,它具有数理金融学和金融计量经济学的双重根源[2]。然而由SV模型含有潜在变量,致使其似然函数极为复杂,求解其估计较困难。为解决这一问题:2002年,JACQULER等[3]将贝叶斯理论与SV模型相结合,首次使用马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法估计,发现其估计效果比似然方法更有效;同年,TSE等[4]实证分析了MCMC估计SV模型的效果,得出在SV模型参数估计方法中MCMC要优于伪似然估计等方法;陈杨林等[2]用MCMC方法求解SV模型对黄金价格指数数据的未来趋势与变化进行了研究,且验证了该模型能够较准确地拟合黄金价格的未来变化趋势和较好地进行预测。而在交通领域中,应用SV模型分析数据较少。其中,李玮峰等[5]应用SV模型对行程时间波动性进行分析,并说明了经济学对分析时间序列特征的模型中,在对道路行程时间波动率的解释上也有很好的可行性。因此,本文通过构建SV模型对路段行程时间进行波动性分析,进而能够揭示行程时间波动结构的特征,对探究出行者行程时间的预测具有现实意义。
1 SV模型和MCMC方法
1.1 模型介绍
在SV模型中,假设波动率是随机游走的,并且服从几何布朗运动
dS(t)=μS(t)dt+σ(t)S(t)dω0(t),
其中μ为标的资产的期望收益率,σ(t)为标的资产的瞬时波动率,dω0(t)为标准布朗运动[6]。在SV模型中,波动率的变化依赖于不可观测的随机过程。
1986年,TAYLOR[7]在说明金融时间对数收益率序列波动模型的自回归行为时,首次建立了标准随机波动率(normal stochastic volatility,SV-N)模型,其离散的表达式为
yt=εtexp(ht/2),εt~i.i.d.N(0,1),
(1)
ht=μ+φ(ht-1-μ)+ηt,ηt~i.i.d.N(0,σ2),t=1,2,…,n。
(2)
式(1)中yt是第t时刻的标的资产对数收益率,干扰项εt独立同分布,且服从标准正态分布,ht表示对数波动率。式(2)中参数μ表示平均波动水平;ηt用于度量波动的扰动程度,独立同分布于N(0,σ),ηt与εt相互独立;φ为持续性参数,能反映当前状态对未来波动的作用程度,当|φ|<1时,认为模型是协方差平稳的;波动ht服从AR(1)过程。在SV-N模型中,均假定误差服从正态分布且平稳,需要估计的参数有均值μ,持续性参数φ以及扰动水平σ2。
用学生t分布代替式(1)中N(0,1)分布,即得到厚尾随机波动率(heavy-tailed stochastic volatility,SV-T)模型,具体形式如下
yt=εtexp(ht/2),εt~i.i.d.t(ω) ,
(3)
ht=μ+φ(ht-1-μ)+ηt,ηt~i.i.d.N(0,σ2),t=1,2,…,n。
(4)
在式(3)(4)中,除εt服从t分布外,其它参数意义与SV-N模型一致。特别地,通常假设εt~N(0,1)或者εt~t(ω)[6]。基于MCMC方法在求解SV模型参数上具有一定优势,以下给出MCMC的基本理论。
1.2 MCMC估计方法
由于数据在维数非常高的情况下,静态的Monte Carlo方法处理速度太慢,计算量太大。所以将Markov过程引入到Monte Carlo模拟中,可得到MCMC(动态Monte Carlo)方法,该方法被广泛应用于高维随机向量的取样[8]。MCMC方法的基本思想可概括为如下三步[9]
(1)在X上选取一个“合适”的Markov链,使得转移核为P(·| ·),其中“合适”主要指π(X)是其对应的平稳分布;
(2)由X中某一点X0出发,用(1)中的Markov链产生序列X1,…,Xn;
(3)对某个m和相对比较大的n,任一函数f(X)的期望估计为
根据以上MCMC方法三个步骤,即可对SV模型中的参数加以求解。基于前述SV-N模型,需要估计的未知参数为μ、φ、σ2,将潜在的波动序列ht,t=0,…,T增加为要估计的参数。因此,参数个数总数为4+T。故联合先验密度为
P(μ,φ,σ2,h0,h1,…,hT)=
参考王以明[9]对SV模型的MCMC估计的方法,假定μ、φ、σ2的先验分布是独立的,并应用与KIM等[10]相同的先验分布:令φ=2φ*-1,其中φ*~Beta(20,1.5),这样φ的先验均值为0.86;令σ2~IG(2.5,0.025),μ~N(0,100),这样σ2的先验均值为0.0167,先验标准差为0.0236。由ηt~i.i.d.N(0,σ2),P(ht|ht-1,μ,φ,σ2) 的函数表达式可以很容易推出。模型的似然函数为L(μ,φ,σ2,h0:T),由yt的条件分布可得似然函数为
基于此,由贝叶斯原理,参数的联合后验分布与似然函数、联合先验分布的乘积成正比,即
P(μ,φ,σ2,h0,h1,…,hT|y1,…,yT)∝
这里可以利用Gibbs抽样方法对SV模型进行抽样模拟,从而估计出模型中的4+T个参数。在Gibbs抽样的构造之前,需假定X的密度函数为π(X),在实际中难以实现,但这并不影响该方法的使用。应用中,可以对i=1,…,n反复利用Gibbs抽样,通常情况下,最后迭代的结果依分布收敛于π分布。抽样的具体步骤如下
(3)设i=i+1,转到第(2)步。
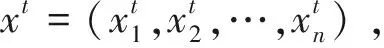
2 实证分析
实例数据选取深圳北环大道新洲立交东往北方向路段1(所处4级道路,长459 m,如图1所示)、北环大道侨香村靠左端西往东方向路段2(所处2级道路,长611 m,如图1所示)的行程时间互联网数据(来源于2018年深圳杯主办方)。数据选取时间段为2018年3月26日至2018年3月28日的行程时间,每条数据间隔2 min,一条路段3天共2160条数据。将用3月26日和3月27日的行程时间数据训练两模型,从而根据模型求解参数对数据进行波动性分析,进而对模型加以选择,拟对3月28日的行程时间进行逐一预测。这里,定义行程时间的对数值一阶差分为行程时间的波动率,计算公式为
yt=(lnTt-lnTt-1)×100,
其中,Tt为t时刻的行程时间[5]。

图1 卫星图(百度地图) Fig.1 Satellite map (Baidu map)
为简要描述路段1和路段2行程时间的基本特征,给出两条路段的行程时间时序图和行程时间的波动率时序图,如图2和图3所示。由图2可知,26日和27日行程时间大小各异,路段1两天的行程时间变化不大,路段2在高峰时段出现明显的起伏状,导致二者不同的主要原因是路段所处道路等级不同。由图3可知,二者行程时间的波动率时序均存在明显的波动率时变性,即在高波动和低波动阶段均出现堆集现象。

图2 路段行程时间时序图Fig.2 Sequence diagram of the travel time of the road section

图3 路段行程时间的波动率图Fig.3 Volatility chart of the travel time of the road section
基于实例中的行程时间,利用频率分布直方图估计行程时间波动率核密度曲线,分析数据的基本特征,结果如图4所示。由图4可以看出,两条路段的行程时间波动率时序分布在均值附近的数值远多于正态分布,表现出尖峰性;在直方图两边分布的数值也比正态分布多,表现出厚尾性。
将两条路段的行程时间波动率时序进行描述性特征统计,结果见表1。由表1可知,二者的波动率时序数据均集中于均值附近;路段1和路段2的峰度分别为26.50、18.79,都大于3,再一次体现了二者的尖峰厚尾特征。

表1 行程时间波动率yt参数表Tab.1 Travel time fluctuation rate parameter table

图4 路段行程时间核密度估计曲线图Fig.4 Nuclear density estimation curve of the travel time of the road section
2.1 SV-N模型的MCMC估计
路段1、路段2的SV-N模型各参数估计结果见表2。表2中,路段1的波动水平参数μ的估计值为2.36,而路段2为2.38,路段1波动水平参数的绝对值小于路段2,说明路段1的行程时间波动程度小于路段2。从波动持续性参数φ角度分析,路段1为0.19,路段2为0.90,二者都小于1,表明二者均平稳且有较强的波动持续性,但相对路段1,路段2比路段1具有更强的波动持续性。从波动扰动水平σ2上比较,由6.98远大于0.55,说明路段1行程时间波动的扰动水平比路段2高。
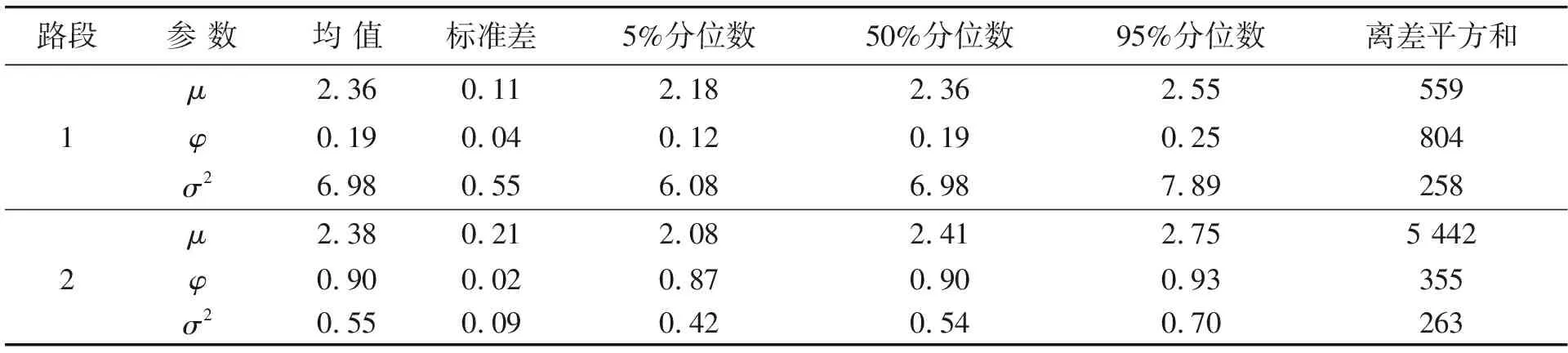
表2 SV-N模型各参数的估计结果Tab.2 Estimation results of various parameters of the SV-N model
2.2 SV-T模型的MCMC估计
路段1、路段2的SV-T模型各参数的估计结果见表3。表3中,路段1、路段2的波动水平参数μ的估计值分别为2.37、2.41,与路段2相比,路段1波动水平参数的绝对值较小,说明路段1的行程时间波动性较低,这与SV-N模型分析结果一致。从波动持续性参数φ角度分析,路段1为0.19,路段2为0.91,二者均小于1,同SV-N模型一样,说明了两路段均平稳且有较强的波动持续性,并且路段2的波动持续性更长。从波动扰动水平σ2上比较,由6.55远大于0.46,同样说明了路段1波动率扰动水平比路段2高。从模型自由度ω的估计看,路段1为33.32,路段2为30.67,再次说明两路段波动率分布非正态。

表3 SV-T模型各参数的估计结果Tab.3 Estimation results of various parameters of the SV-T model
2.3 模型选择
结合表2(SV-N)、表3(SV-T)中的模型参数的估计结果,从单条路段分析,对比SV-N模型和SV-T模型拟合实例数据的效果。对于波动水平μ的估计值来说,无论是路段1还是路段2,其绝对值均表现为SV-T模型的估计值更大,说明路段1、路段2在SV-T模型下表现出来的波动性均强于SV-N模型。就可持续性参数φ的估计值而言,SV-N模型的φ的估计值在0.20左右,SV-T模型的φ的估计值在0.90偏上,说明路段2比路段1更具有波动聚集性效应;从整体上来看,SV-T模型中φ的估计值比SV-N模型的大,说明SV-T模型比SV-N模型能更好地刻画两路段波动率的波动持续性。特别地,对于评价扰动水平的参数σ2来说,当可持续性参数φ越大,而σ2越小时,波动的过程越易预测。在表2和表3中,SV-T模型的σ2值均小于对应的SV-N模型中的值,说明SV-T模型的拟合效果优于SV-N模型。

图5 路段Q-Q图Fig.5 Road section Q-Q diagram
基于前述分析基础上,利用两路段在SV-N模型和SV-T模型标准化残差的行程时间波动率Q-Q图来直观验证二者的优劣,如图5所示。从图5可以看出,和SV-T模型拟合的标准化残差基本都落在y=x直线上,相对SV-N模型而言,两路段在SV-T模型拟合下效果更好。
2.4 行程时间预测结果
由以上对路段1、路段2的波动性分析可知,SV-T模型更能描述路段1、路段2的行程时间波动性。图6为基于SV-T模型对路段1和路段2的行程时间(3月28日)预测结果。图6可以看出,SV-T模型的预测效果非常好,这里计算了各路段实际值与值的MSE,路段1为22.68,路段2为70.04。
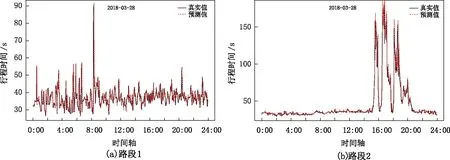
图6 行程时间预测结果Fig.6 Travel time prediction results
3 结论
本文选取北环大道所处不同道路等级的两条路段26日和27日行程时间数据,分别构建SV-N模型、SV-T模型,并利用MCMC方法求解模型参数,对比模型拟合效果。结果表明:两条路段的行程时间均呈现尖峰厚尾特性;波动水平参数显示,道路等级较高的行程时间波动度显著,同时道路等级较高的波动持续性更强;从扰动波动水平角度看,道路等级低的相对较高。经实例分析证实,在刻画波动率的波动特征效果上,SV-T模型优于SV-N模型。选用SV-T模型对3月28日全天的行程时间进行逐一预测,两条路段预测效果较为精确。

