Fermi伽马射线暴的光谱能量关系
骆娟娟,米立功
(黔南民族师范学院 物理与电子科学学院,贵州 都匀 558000)
1967年科学家们偶然发现了伽马射线暴,伽马射线暴简称伽马暴(GRBs),是宇宙中高能伽马光子急剧增加又急剧衰减的现象[1]。它是宇宙中最明亮最遥远的光源[2-4],可以作为早期宇宙学的探针。过去的几十年中,科学家们发现了很多光谱能量关系[5]。例如:lag-luminosity关系,variability关系Amati关系[6-9],Ghirlanda关系[7]和Yonetoku关系[5-10]等。
本文是基于Fermi卫星经过一定选择标准的数据样本,主要对峰值能量-均质能量和峰值能量-均质光度做再修订,此外提出了长短暴[11]可以通过这两种关系分类[6]的结论。峰值能量Epeak指一个完整的暴在E2N(E)&νFν能谱中出现的能量最高值。均质能量Eiso指一个完整的暴所具有的各向同性能量。均质光度Liso指一个完整的暴所具有的各向同性光度。
1 样本选择和计算
本文收集了Fermi卫星2010年12月至2018年12月红移已知的GRBs的数据样本。共有84个已知红移的Fermi暴,其中有81个长暴,3个短暴。
1.1 均质能量的计算
实际的计算过程中,采用了平滑幂率的光谱拟合:
其中,Φ表示光子能谱分布函数,E0表截断能。
热辐射流量Sbolo和观测流量S满足[12]:
1.2 均质光度的计算
本文使用Band函数拟合。单位时间,单位面积内观测的光子个数Pph满足[12]:
分三种情况讨论,Pph满足关系式[12]:
(1)Emax≤(α-β)E0,
(2)Emin≤(α-β)E0≤Emax,
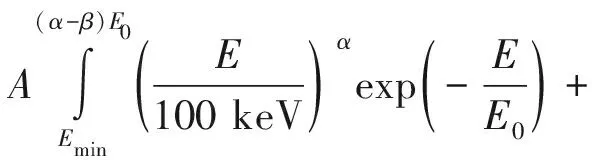

(3)Emin≥(α-β)E0,

不分区间推演出不同的归一化常数A的值:
(1)Emax≤(α-β)E0,
(2)Emin≤(α-β)E0≤Emax,
(3)Emin≥(α-β)E0,
峰值能量通量erg/cm2/s,可以通过下面的公式计算:
同样地,分成三个不同区间计算Fγ[13-15]。
k修正的光度Liso满足:
修正函数[16-17]:
能量比例[18]Amati和Yonetoku关系:

本文计算过程中假定宇宙学参数满足如下关系:H0=71 kms-1Mpc-1,ΩM=0.68,ΩΛ=0.32。
2 数据分析
2.1 Eiso和Liso分布图
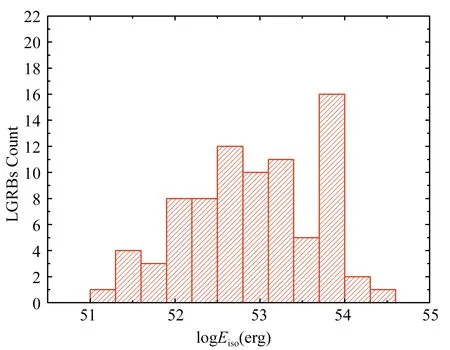
图1 Fermi长暴logEiso的统计分布直方图Fig.1 The statistical distribution histogram of Fermi long bursts logEiso

图2 Fermi长暴logLiso的统计分布直方图Fig.2 The statistical distribution histogram of Fermi long bursts logLiso
第1部分详细介绍了Fγ、Eiso、Liso的计算过程,误差通过误差传递来计算。图1可以得出,从logEiso=50.5到logEiso=55 中间一共有12 个方格。Eiso的均值满足2.02×1054 erg。图2可以得出,从logLiso=49到logLiso=53.5 中间一共有12 个方格。Liso的均值满足2.32×1052 erg/s。即大多数伽玛暴的平均能量为1054erg,平均光度为1052erg/s量纲。
2.2 Ep,i-Eiso和Ep,i-Liso更新关系
Amati关系满足[6-8]:
最初的Amati关系:K≈95,m≈0.5,用来限制宇宙学参数,解释不同喷流模型的快速辐射过程,和理解不同类型伽玛暴的本质区别。
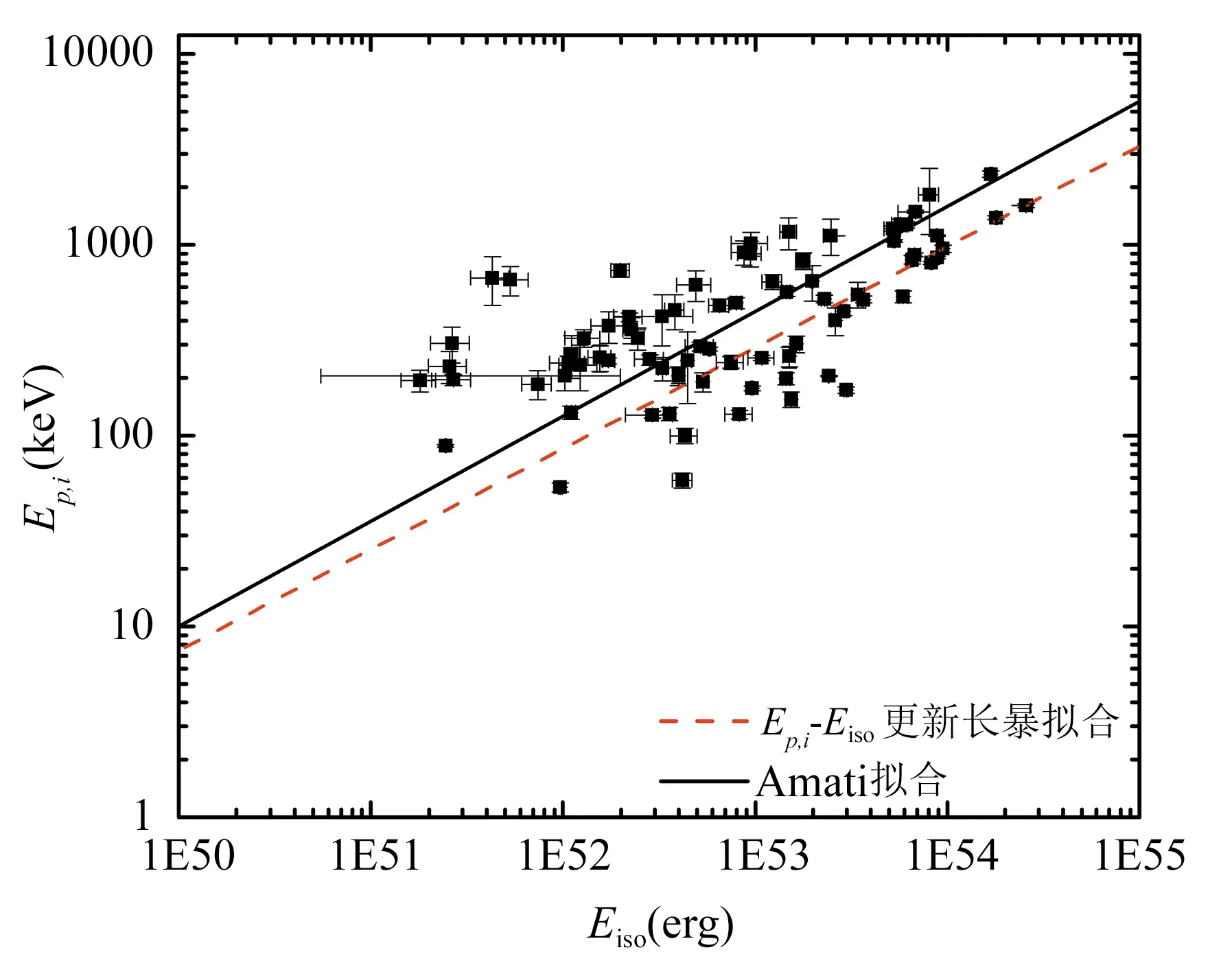
图3 基于Fermi长暴的Ep,i-Eiso平面Fig.3 Ep,i-Eiso plane which is based on Fermi long bursts

图4 基于Fermi长暴的Ep,i-LisoFig.4 Ep,i-Liso plane which is based on Fermi long bursts
图3中描绘出了81个已知红移的Fermi[19]长暴数据样本,实线是Amati02参数进行的线性拟合,点线是基于本文数据点的线性拟合。
Yonetoku关系[5]:
最初的Yonetoku关系:A≈37.15,p≈1.75,图4中描绘了81个已知红移的Fermi长暴数据样本,实线是Yonetoku04参数进行的线性拟合,点线是基于本文数据点的线性拟合。
表1列出了基于Fermi长暴,本文与Amati02和Yonetoku04对比拟合数据。经分析本文的拟合数据更符合观测实际。

表1 对比拟合表Tab.1 Contrast fitting table
2.3 Ep,i-Eiso和Ep,i-Liso的长短暴分类

图5 基于Fermi卫星的Ep,i-Eiso平面Fig.5 Ep,i-Eiso plane which is based on Fermi satellite

图6 基于Fermi卫星Ep,i-Liso平面Fig.6 Ep,i-Liso plane which is based on Fermi satellite
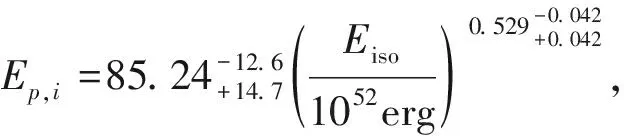
2.4 红移分布和能量比例
为了更好地检测能量关系,图7中统计了长短暴的红移分布直方图。长暴的红移偏大,平均值是2。短暴的红移偏小,平均值是0.5。图8中分别给出长短暴的能量比例关系,即ξ1和ξ2关系。经分析在z-Energy ratio平面[20],长暴的集中区域点红移偏大,而短暴的集中区域红移偏小。虽然短暴只存在三个数据不足以拟合曲线,但就目前短暴的分布来看,图7和图8相互对应[21],这是由于长暴比短暴更亮,因此可以看到更远的长暴[16-17]。

图7 基于Fermi卫星的长短暴红移分布直方图Fig.7 The redshift distribution histogram of long and short bursts which is based on Fermi satellite

图8 z-Energy ratio平面Fig.8 In z-Energy ratio plane
3 总结和讨论
首先,本文的所有数据都是基于Fermi卫星的,因此观测到的峰值能量比swift卫灵敏度高。其次,本文收集了Fermi卫星最近8年的数据样本,数据样本比较新,因此研究具有较大的意义。
基于最近8年的Fermi数据样本[20],本文首先分析了Amati[18]关系和Yonetoku关系,得到了表一的拟合参数并和前人的拟合参数做了对比,更新了能量关系和光度关系。其次,计算了能量和光度的分布直方图,得到了现有的GRB的辐射量级范围[18]。基于目前的统计来看,长暴和短暴有着互相独立的能量分布函数。跟前人的结果对比,有着微小差异。产生这些差异的可能原因是探测器的灵敏度变高,选择的数据样本更大造成的。最后,本文给出了长短暴满足的红移分布图,得到了长暴的红移值偏大,短暴的红移值偏小的结论。随着今后Fermi探测器及其它探测器数据的不断更新,有望可以找出更好的相关性来区分长短暴,进而得出长短暴的本质属性。

