水平三向撞击流混合器不同喷嘴夹角流场特性数值模拟

张建伟, 高 博, 冯 颖, 马繁荣

(沈阳化工大学 能源与动力工程学院, 辽宁 沈阳 110142)

自从Elperin[1]提出撞击流概念以来，由于撞击流具有促进微观混合和强化相间传递的特性[2]，被广泛应用于液液混合、脱硫、水煤浆气化、超细粉体制备等多个工业领域[3-6].目前，不同喷嘴数量的撞击流混合器已被广泛研究.张建伟等[7]利用激光多普勒测速系统测得两喷嘴撞击流混合器流场速度分布.李伟锋等[8]发现了撞击面的不稳定性和驻点偏移规律.Kind[9]等和Rew[10]等的实验结果均表明撞击流驻点的位置由两喷嘴的出口动量比决定.杨侠[11]利用数值模拟的方法得出三喷嘴混合器径向速度分布.张珺等[12]通过碘化物-碘酸盐平行竞争反应体系验证了三喷嘴混合器混合效果优于两喷嘴撞击流混合器.杨侠等[13]利用数值模拟得到了四喷嘴撞击流混合器的径向速度分布于压强分布,验证了四喷嘴撞击流混合器混合效果优于两喷嘴混合器.多喷嘴撞击流混合器相较于传统撞击流混合器能够实现多种物料的混合且混合效果优于传统撞击流混合器.代正华等[14]等通过实验和模拟的方法研究四喷嘴对置式撞击流的流场特性，并通过数值模拟的方法得到了四喷嘴混合器回流比分布情况.目前对三喷嘴撞击流混合器喷嘴分布形式的研究较少,本文利用CFD数值模拟方法对不同喷嘴夹角的水平三向撞击流混合器的流场特性进行分析.

1 数值模拟

1.1 物理模型

三喷嘴撞击流混合器为立式圆柱形筒体，混合器高度H=500 mm，直径D=130 mm，出口位于混合器上方，出口直径D=30 mm，入口距离反应器顶部250 mm，入口喷嘴直径d=10 mm，三喷嘴与中心圆相切，中心圆的直径即为当量喷嘴间距L，张建伟等[15]在探究三喷嘴撞击流混合器流型时得出当L=2d时混合效果最佳，故取L=2d=20 mm.固定X轴方向喷嘴a，其余两喷嘴b、c关于X轴对称且夹角为α，取α分别为60°、90 °、120°、150°、180°布置.物理模型如图1所示.

图1 撞击流混合器结构示意图Fig.1 The layouts of impinging stream mixer

1.2 网格划分及边界条件

使用ICEM软件对模型进行网格划分.由于入口附近结构复杂，采用非结构化四面体网格，其余区域采用结构化六面体网格，总网格数为1 216 850，网格质量大于0.4.使用Fluent15.0进行模拟，采用基于压力的隐式求解器，速度和压力耦合项使用SIMPLEC算法，为提高计算精度，采用二阶迎风格式计算.出口边界条件定义为Outflow；壁面采用标准函数且无相对滑移；入口边界条件定义为Velocity-Inlet；入口流量为0.5(m3·h-1),即入口速度为1.77 m/s，采用20 ℃的水作为模拟介质.

1.3 控制方程

Realizable k-ε模型和标准k-ε模型均可用于多射流撞击式喷嘴湍流流动的数值模拟计算[16]，由于Realizable k-ε模型能够更好地模拟大尺度的涡结构，故选用Realizable k-ε模型，其输运控制方程如下：

(1)

动量方程：

(2)

(3)

(4)

运输控制方程：

(5)

(6)

其中:σk=1.0，σε=1.2，C1=max[0.43,η/(η+5)]，η=(2EijEij)1/2k/ε，Eij=(∂ui/∂xj+∂uj/∂xj)/2，μt=ρCμk2/ε，Cμ=(A0+AsU*k/ε)-1，A0=4.0，As=61/2cosφ，φ=1/3cos-1(61/2W)，W=EijEjkEkj/(EijEij)1/2

上述各式中ρ为流体密度；v为运动粘度；xi、xj为各坐标分量；Gk为平均速度梯度所产生的湍动能；σk、σε为湍流动能k和湍流耗散率ε的湍流普朗克数；μt为湍流黏性系数；Eij、Ejk、Ekj为不同方向的时均应变率；x、y、z为空间之间坐标系；u、v、w为质点的速度分量；t为时间；ui、uj为速度矢量的分量；U*为平均旋度；E为能量.

1.4 网格无关性检验

为进一步验证模拟准确性，排除网格因素影响，验证结果如图2所示.

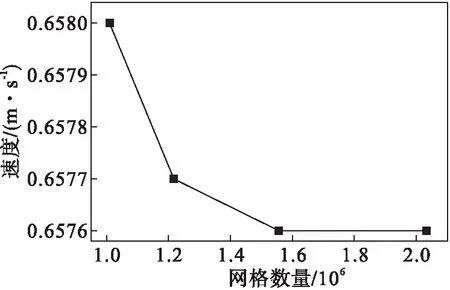
图2 不同网格数量下出口速度大小Fig.2 The outlet velocity under different cell number

图2对网格数分别为1 009 889、1 216 847、1 556 287、2 032 480的情况下出口速度大小进行比较，结果表明：当网格数量大于1 200 000时，出口速度差小于2 %.为节省计算时间，选用网格数量为1 216 850的网格划分方法.

2 结果与讨论

2.1 不同α角撞击流混合器湍动能分布

湍动能是衡量混合效果优劣的重要指标，较大的湍动能值表示流体湍动较为剧烈，增强流体间无规则运动，从而促进物料间混合效果.不同夹角的水平三向撞击流混合器湍动能分布如图3所示.

图3 撞击流混合器湍动能在Z=0轴截面分布Fig.3 Distribution of turbulence energy in impinging stream mixer at Z=0 axis section

撞击流混合器的高湍动区域在撞击面的中心处，且湍动能分布近似关于X轴对称.随着α角增大，湍动能沿X轴方向扩散越明显，湍动能峰值逐渐降低.当夹角α=60°时， 湍动能如图3(a)所示，喷嘴间夹角较小，流体在X轴方向流量较大，使湍动能沿Y轴方向扩散，湍动能在中心区域近似椭圆形，相较于其他夹角的撞击流混合器湍动能更为集中，因此，在撞击面形成的湍动能峰值也最大，流体间撞击较为剧烈.当α=120°时，如图3(c),由于喷嘴均匀布置，湍动能分布较为均匀，湍动能沿喷嘴夹角方向扩散，湍动能中心处呈三角形“靶式分布”[17].图3(e)中喷嘴夹角α最大，湍动能峰值最小，湍动能沿X轴正向扩散趋势越明显.

图4为不同喷嘴夹角撞击流混合器沿X轴方向湍动能曲线.由图4可知：当α=60°时，湍动能到达峰值后迅速减小，这是由于喷嘴夹角较小，促使湍动能向Y轴扩散，与图3(a)规律相符且湍动能峰值位置距离原点较远；当α=90°时，湍动能峰值发生偏移，但偏移量较小；当α≥120°时，湍动能峰值位于原点处；相比α=60°，当夹角α增大时，当湍动能到达峰值后，X轴方向湍动能下降较为平缓；当α=180°时，湍动能峰值最小且变化趋势也较为平缓.

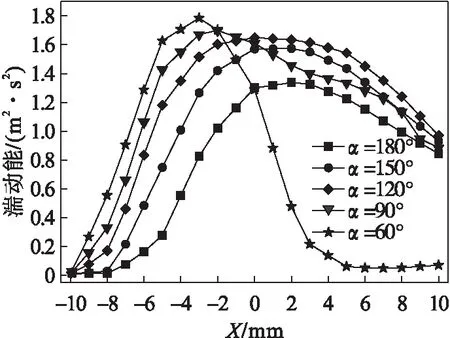
图4 X轴方向湍动能分布Fig.4 X-axis turbulent kinetic energy distribution

图5为撞击流反应器在撞击面上径向湍动能分布.不同喷嘴夹角的撞击流混合器在撞击面处Z轴方向上的径向湍动能分布规律相似，呈单峰分布，且关于直线Z=0对称.不同喷嘴夹角条件下具有相同的径向湍动能分布规律，且与张建伟等[18]研究所得到的径向湍动能分布规律相同，在Z=0处湍动能最大，即在驻点位置湍动能达到峰值.

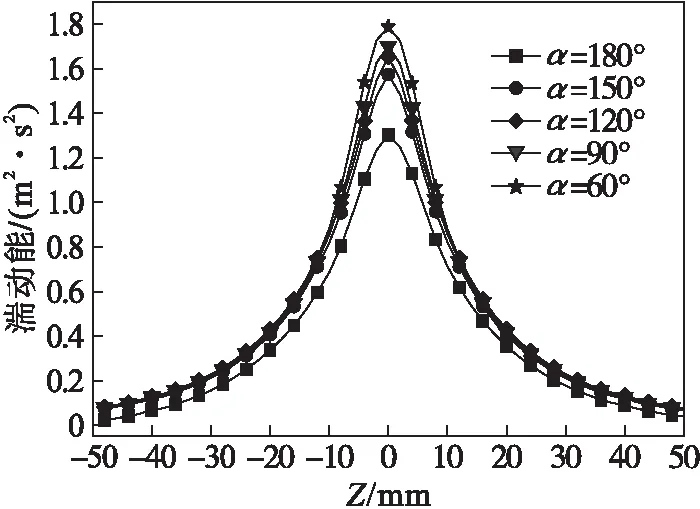
图5 径向湍动能分布Fig.5 Radial turbulent kinetic energy distribution

2.2 撞击流混合器驻点与速度分布

图6为不同α角三喷嘴撞击流混合器在Y=0轴截面的速度分布云图.

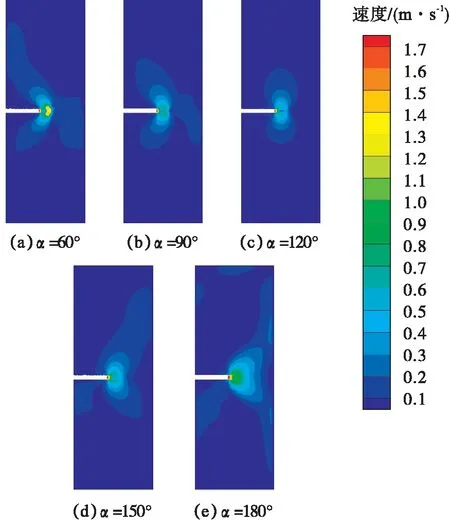
图6 撞击流混合器在Y=0截面速度分布云图Fig.6 Velocity distribution of the impinging stream flow mixer at Y=0 cross section

由图6可知：流体经过撞击后产生径向速度，其中心区域速度分布情况在Y=0轴截面上近似关于X轴对称.由图6(a)可知：当α=60°时，流体进入反应器后，由于X轴正向两喷嘴一侧夹角较小，两喷嘴一侧流体先发生碰撞形成汇流，产生较高的轴向速度，同时使流体向Z轴方向偏移，在汇流处产生较高的偏移速度.流体在驻点位置撞击后产生径向速度与汇流时产生的偏移速度使得流体经过撞击后向X轴负向运动，同时促进了流体在撞击区的不规则运动，从而提高流体间混合效果.从图6(b)可以看出：当夹角α=90°时，两喷嘴一侧产生的偏移速度较小，流体产生撞击后仍产生向X轴负向运动偏移速度，与α=60°相比，偏移效果明显降低.当α=120°时，如图6(c)所示，喷嘴分布均匀，速度分布关于Z轴对称，且与三喷嘴混合器漏斗状流型[15]相符合.当α≥120°时，如图6(d)、(e)所示，夹角α越大，流体向X轴正向运动越明显，且速度分布范围越大.当α=180°时，在浸没状态下撞击流反应器的速度分布情况与张珺等得到伞状流型[19]相似.

撞击流混合器X轴方向速度曲线如图7所示.当α<120°，由于喷嘴间夹角α较小，一侧流量较大，速度最小值均不在原点处，撞击流混合器驻点产生偏移，且α越小驻点位置越远离原点.当α≥120°时，流量分布较为分散，驻点位于原点处.与图4中湍动能峰值偏移规律相同，即湍动能峰值出现在驻点处.当α=60°时，X轴速度分布规律与其他夹角混合器分布规律不同，X轴正向存在较大的轴向速度，进一步验证了图6(a)中由于喷嘴夹角较小而产生的汇流.与α=60°相比，当α=90°时喷嘴夹角较大，b、c喷嘴形成的汇流规模较小，形成了较小的X轴向速度.但由于同样产生了汇流，影响两侧动量比，从而使驻点发生偏移.当α≥120°时，流体经过撞击后，X轴速度变化规律基本相同，且速度大小与夹角α成正比.

图7 X轴方向速度分布Fig.7 X-axis velocity distribution

图8为撞击流混合器径向速度分布图.如图8所示，不同喷嘴夹角条件下具有相同的径向速度分布规律，均为双峰分布[13]，径向速度分布关于直线z=0对称.当α=120°时，径向速度峰值最小，且驻点处速度最小.当α<120°时，径向速度峰值随夹角α增大而减小，当α≥120°时，径向速度峰值随夹角α增大而增大.当α=180°时，混合器径向速度最大，由图4已知湍动能较小，这是由于喷嘴a没有受到撞击，此时喷嘴a射出的流体经过驻点后仅对流场起到冲击作用，增大流体的流动性.

图8 径向速度分布Fig.8 Radial velocity distribution

表1为撞击流混合器径向速度均方根差σ[20]，选取撞击面上径向100个点的速度大小计算速度均方根差σ，其表达式为：

(7)

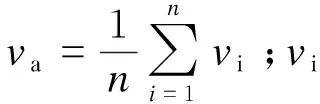
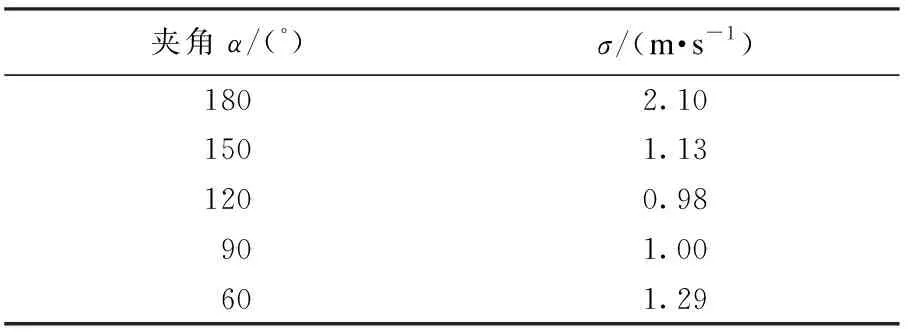
表1 径向速度均方差

速度梯度大小与混合效果成正比[13]，利用速度均方差σ衡量速度梯度，速度均方差σ越大，混合效果越好.当α=120°时，速度均方差最小，混合效果较差.当α≥120°时，速度均方差与α成正比，α越大混合效果越明显.α<120°时，α越小速度均方差越大，混合效果越明显.当α=180°时，σ=2.10 m/s，大于α=60°时的速度均方差.结合湍动能与速度分布情况，当α≥120°时，X轴喷嘴撞击作用减小，但对流场速度影响较大.因此，结合湍动能和速度分布,对不同角度三喷嘴撞击流混合器，当α=60°时，混合效果最佳.

3 结 论

(1) 通过对不同夹角水平三向撞击流混合器模拟结果的分析可知α=60°，X轴向湍动能变化较大，α≥90°，X轴向湍动能过驻点后变化趋于平缓，且X轴湍动能分布规律相似.湍动能峰值出现在驻点处且随α增大单调递减.混合器径向湍动能分布规律与喷嘴夹角无关.

(2) 混合器速度分布随夹角增大，先减小后增大，α=120°速度最小.混合器径向速度分布规律与喷嘴夹角无关，均成双峰分布.α=180°脉动速度σ=2.10 m/s大于α=60°时σ=1.29 m/s，对于不同夹角三喷嘴撞击流混合器，当α≥120°时，X轴向喷嘴对驻点的撞击作用逐渐减小，速度衰减减弱，增大了对驻点的扰流作用，增强流体扩散性.

(3) 随着喷嘴间夹角α的改变，混合器内驻点位置也发生变化，α<120°驻点随α变化产生偏移，且α越小驻点偏移距离越大，α≥120°驻点位于原点处.