多元函数泰勒公式及其应用
黄贤峰,史亳徽
(阜阳师范学院数学与统计学院,安徽阜阳 236037)
泰勒展式是数学中一个极为重要的概念,是微分学理论的最一般情形,具有化繁为简、化难为易的功能。同时,其在多元函数逼近、计算机图像学及工程近似计算等领域具有较为广泛的应用。其中,一元函数泰勒展开式的研究已相当成熟,如利用一元函数泰勒公式求解极限、利用泰勒展开式巧解行列式以及利用泰勒展开式求函数图像的渐近线等。而多元函数泰勒展开式的问题研究想对较少,而多元函数的研究更加具有实际价值,因此该文将在一元函数泰勒展开式的基础上,对多元函数的泰勒展开式展开研究。首先,对多元泰勒展开式的基本知识进行了归纳和总结。其次,由于多元泰勒展开式在展开时比较复杂,因此该文将借助MATLAB 实现这一过程。再次,借助张量与张量积运算为泰勒展开式引入一种新的表现形式,使其更加简洁直观,便于理解和记忆。最后,借助多元泰勒展开式在数学、物理学及经济学中的实际问题说明其巨大的应用价值。
1 预备知识
下面将给出多元函数和多元函数泰勒展开式的定义。
定义1(二元函数) 设D 是平面点集,R 为实数集,f 是一个对应规则,若对于D 中的每一个(x,y),通过对应规则f,在R 中有唯一的点与之对应,则称f 是定义在D 上的一个二元函数。它在的值为z,记为:
z=f(x,y),(x,y)∈D⊂R2
也可以说是从到的一个映射,记作:
f:D→R,(x,y)→z=f(x,y),
其中,称D 为该二元函数f 的定义域,像集f(D){z|z=f(x,y),(x,y)∈D}称为值域。
定义2(n 元函数)设D 是Rn的一个非空子集,f 是一个对应规则,若对于D 中的每一个点P,通过对应规则f,在R 中有唯一的点u 与之对应,则称f 是定义在D 上的一个n 元函数。它在P 点的值为u,记为u=f(P),P∈D⊂Rn
也可以说是从D 到R 的一个映射,记作:
定义3 设函数f:Rn→R,x∈Rn,f 在点x 的某个以δ为半径的邻域内S=U(x,δ)⊂Rn具有直到(n+1)阶的连续偏导数,则对Ax'∈S,有
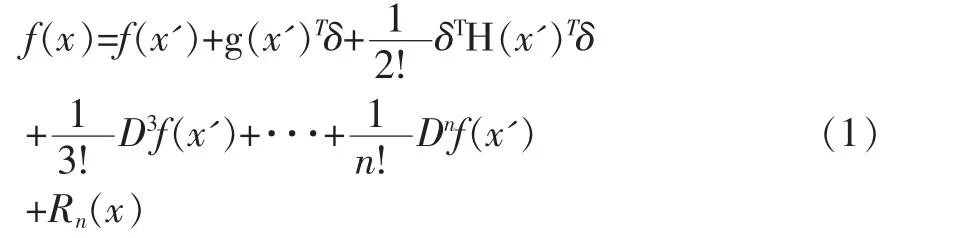
其中,δ=(δ1,δ2,···,δn)T
=(x1,x2,···,xn)-(x'1,x'2···x'n),

公式(1)称为以(x-x')的幂展开的带有拉格朗日型余项的n 阶泰勒公式,Rn(x)称为拉格朗日余项,且有

其中,(3)式称为佩亚诺型余项。
此时若取x'=0,则ξ 在0 与x 之间,故可令ξ=θx(0<θ<1),使泰勒公式变为更为简单的形式,即带有拉格朗日余项的麦克劳林公式。
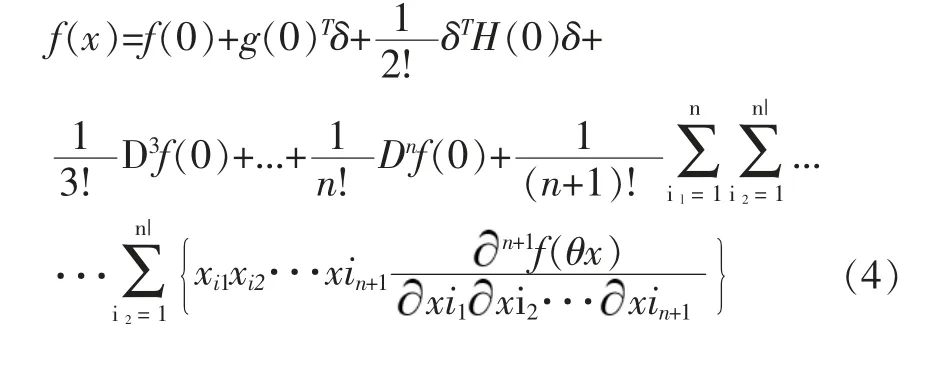
当Rn(x)要求不大精确时,n 阶泰勒公式亦可表示为
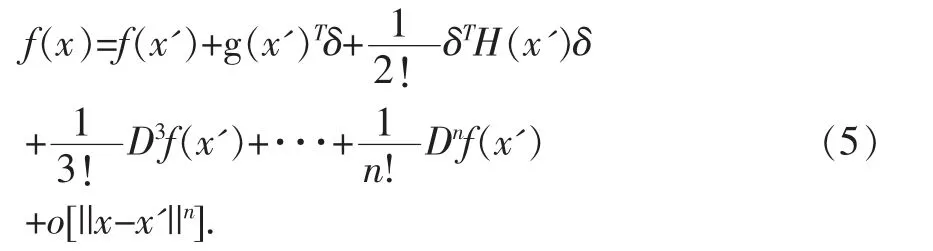
公式(5)称为以(x-x')的幂展开的带有佩亚诺型余项n 的阶泰勒公式。若取x'=0,则得到带有佩亚诺型余项的麦克劳林公式
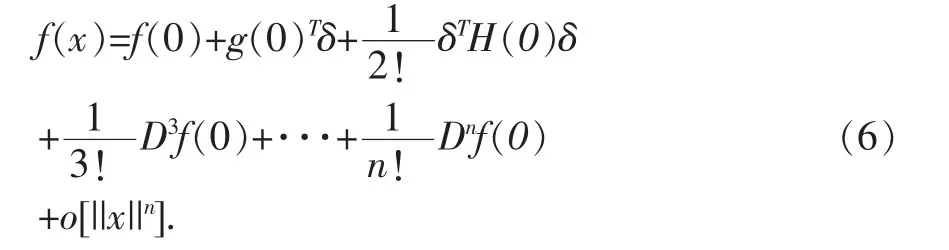
由(4)或(6)可得到近似公式

2 多元函数泰勒展式的张量表示
从功能上说,张量[5]可以理解为多维数组,其中零阶张量表示标量(数量),一阶张量表示向量,也就是一维数组;n 阶张量可以视为为一个n 维数组。
该文为了问题说明的方便,以三元函数的三阶泰勒展式为例展开说明。现假设函数f (x, y, z)在点p0(x0,y0,z0)的某个以δ 为半径的邻域U(p0,δ)内具有三阶连续偏导数。对于Ap(x, y, z)∈U(p0,δ),做差分计算得到:
Δx=x-x0;Δy=y-y0;Δz=z-z0.即Δp=(x-x0,y-y0,z-z0)T.

代入三元函数,则可得泰勒展式的基本形式为:

同理,我们可以得出n 元函数的泰勒展式的一种比较简洁和直观的表达形式,只是过程相对来说比较复杂,但是仍然可以实现。
3 多元泰勒展式的实际应用
由于泰勒展式在数学、物理学及经济学等领域应用较多,所以下面以多元泰勒展式为例
对于三元函数f(x,y,z)在点
x=a,y=b,z=c 邻域的泰勒展式为:
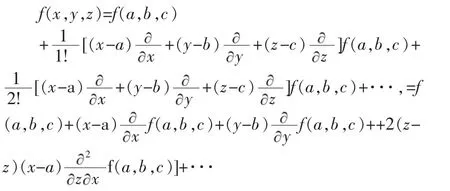



ρ 称为体系的电偶极矩[6],张量Dij称为体系的电四极矩。
综上,得电荷体系激发的在远处的多极展开式为
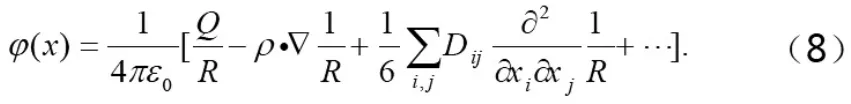
通过对多元泰勒展式在物理学领域这一实例的分析,足见其应用价值。
4 结语
在分析多元泰勒展开式的基础上,本文给出了元函数带有拉格朗日型余项与带有佩亚诺型余项两种形式的泰勒公式; 同时也给出了元函数带有拉格朗日型余项与带有佩亚诺型余项两种形式的麦克劳林公式。利用MATLAB 软件直观分析了一个多元函数与其泰勒展开式之间的区别和联系。并借助张量知识给出了多元泰勒展开式的另一种较为简洁、直观的表现形式。最后,具体分析多元泰勒展开式在实际生活中的应用,展示其重大的应用价值。因此,该文一方面可以促进泰勒展开式相关理论知识的学习;另一方面,对于实际的生产生活具有一定的应用价值和指导意义。

