小学数学教学中数形结合思想的策略初探

梁艳红

摘  要：数与形是数学中两个最基本的教学对象。它们在一定条件下形成转化并发生联系，我们称之为“数形结合”。数形结合思想的教学发展，是为了将抽象的数学语言转化为直观的图形、符号等，从而帮助学生从容的发现其中规律，探寻到解题方法。对于思维意识尚未得到全面发展的小学阶段学生来说，解决那些抽象的数学问题，存在着相对的难度。因此，教师应在课堂教学中，有意识地引导他们将题目中的数与形相互结合，从而形成所对应的数学结合思想，使他们在提升数学结题能力的同时，提升数形结合思维的发展。

关键词：小学数学;数形结合;策略初探

【中图分类号】G623.5    【文献标识码】A       【文章编号】1005-8877（2019）21-0121-01

1.以形助教，營造快乐学习氛围

小学阶段学生的思维，以具象为主导占据主观意识的主体。因此，教师在教学中应着重关注与教学活动的直观引导，灵活设计教学环节，通过形象化的图形来助力课堂教学，从而应造出愉快的学习氛围，促进学生对知识的感悟，积累数学思维理性的解读。

例如，在《分数的初步认识》教学中，教师可以利用卡通形象图案，帮助学生乐于接受平均分配的意义，深度理解平均分的基本性质。其次可以设计动画视频课件，把生日情境生动呈现，让学生通过把蛋糕（圆）平均分成若干份，其中的1份就是这个蛋糕（圆）的几分之一。这样的教学活动使得书面知识生动起来，也将抽象的分数理解，变成更加具体化、形象化的认知。之后还可以引导学生利用折纸的方式折出。实践操作的过程，让学生形成更加深刻的数形结合的良性感知，使学生在图形、视频、操作中领悟分数的本质，以及一边观察、一边动手、一边思考、一边判断的综合能力，使得分数基础知识得以快速的构建，形成乐学、易学的快乐课堂。

2.以形促思，助力数学思维发展

陶行知先生的教育名言“创造始于问题”，不仅揭示了问题提出的魅力，更揭示了创造解决的活力。而数形结合这个思想犹如学生行走中的“拐杖”，能很好地促进学生对于问题提出的意识形成，促进他们数学问题的辨析能力，从而促使学生的学习更具活力与动力。

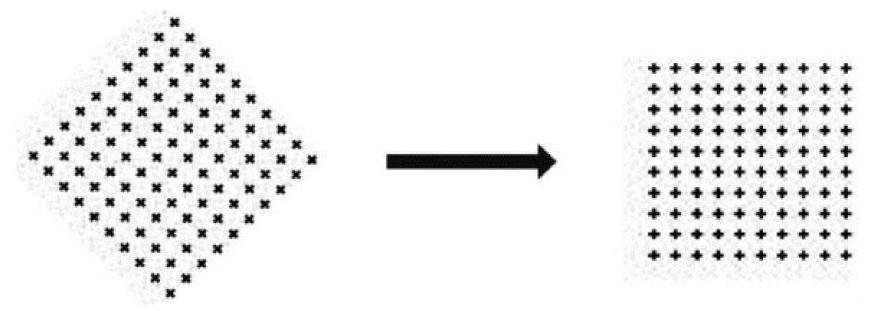
例如，在五年级下册《数与形》中“1+2+3+…+100+99+98+…+2+1”一题为例，由于涉及数字较多，计算过程较长，教师可以采用数形矩阵的方法将1～10形成回环加法来讲解。（如图）用黑点的数量代表数字，引导学生认识1～10的回环加法可以转化成右边的10×10的矩阵图形，最后采用类比推理的手法自然可以直观地计算出结果。数与形，在数字知识的架构中是不可分割的对立面，二者之间形成共同体能够有效解决实际问题。这对促进小学生数量、等阶、递进等关系的理解与分析拓宽了思路，同时也形成了扬数之长、取形之优、融会贯通、相得益彰的良好效益。

3.数形结合，促进学习能力拓展

数形结合的思想，能够实现课堂教学中数形思维的巧妙迁移，从而让学生学习的视角更加开阔，使课堂的教学得到最为科学的发展。当前的小学数学课堂中，因其教材中蕴含了无处不在的形态丰富、颜色鲜艳的情境图片，使得教师的教学不仅能够彰显可爱的图形之柔美，还能够呈现学生数学素养提升的兴趣保障。因此，教师应更加充分的利用其教材中的有效图案，为学生构建数形结合思想的学习概念，使他们能够在最直观的感性认知中，形成更加丰富的知识经验积累。

例如，《圆的面积》一节，教师可以借助教材中撞色图形的分析，将“圆”通过分割、拼合等办法，转化成我们已知的图形，从而推导出圆的面积计算公式。（如图）

最后通过对图形的分析，引导学生结合图形理解长方形的面积等于圆的面积，长方形的长相当于圆周长的一半，宽相当于圆的半径，最后得出圆的面积=圆的周长的一半×圆的半径。“以形助数”或“以数解形”，将数学知识由粗浅变得深刻，从而使学生更加容易接受和理解知识的本质，拓宽了学生解决问题的思路。

总之，在小学数学课堂中渗透数形结合的教学思想，能把抽象的数学理论转化成更加形象的数学概念，从而帮助学生在解决复杂数学问题的同时，轻松掌握、简化算法。通过数学结合思想的具体运用，不仅能够提高教师的课堂教学质量，还能够进一步提升学生的逻辑思维能力和学生的综合数学素养。

参考文献

[1]韩英，殷爱明.数形结合在小学数学教学中的运用[J].学周刊，2019（1）：83-84

[2]庄志鹏.探讨小学数学教学中数与形的“有机结合”[J].课程教育研究，2019（10）：141