教学：在学生的困难处展开——林俊老师《两条直线的位置关系》一课赏析

李雪玲

摘要：林俊老师执教的《两条直线的位置关系》一课，抓住学生学习的困难展开教学，教得准、教得深、教得透。具体地，设计了“整体分类”环节，从学习的争议处引入;设计了“认识平行”环节，从学习的浅表处追问;设计了“认识垂直”环节，从学习的疑惑处澄清;设计了“沟通联系”环节，从学习的混沌处完善。

关键词：学习困难教学设计两条直线的位置关系

最近，听了特级教师林俊老师执教的《两条直线的位置关系》一课，颇受启发。纵观此课，林老师抓住学生学习的困难展开教学，教得准、教得深、教得透。具体表现在如下四个方面：

一、整体分类：从学习的争议处引入

【教学过程】

师（出示一条直线）直线有什么特点？

生是直的，可以无限延长。

师（出示另一条直线，并让它顺时针转动）如果有两条直线，又能组成哪些图形？组成的图形又有什么特点？（板书课题）今天，我们就来研究——两条直线的位置关系。

（学生思考。）

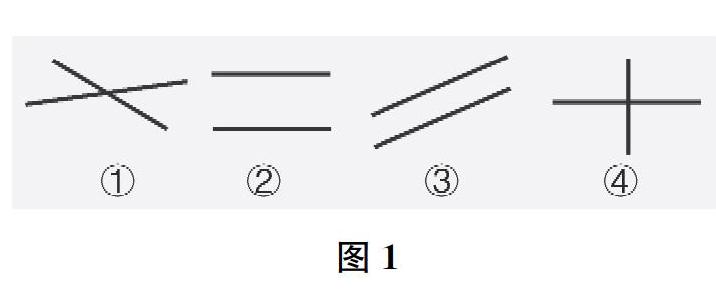
师（出示图1）你能把它们分成两类吗？为什么这样分？

生①和④为一类，因为它们相交了;②和③为一类，因为它们不相交。

生①和④相交于一点，形成了四个角。

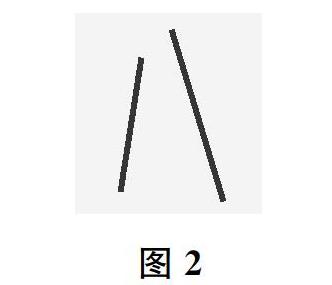
师像①和④这样，两条直线有一个公共点叫作两条直线相交，这个公共点叫作它们的交点。像②和③这样，两条直线在同一个平面内不相交叫作两条直线互相平行，其中一条直线就是另一条直线的平行线。（出示图2）这一组直线属于哪一类？

生相交。

生平行。

师明明没有相交，你为什么说是相交？

生直线可以延长，延长以后就相交了。

（教师课件演示两条直线延长后相交于一点。）

【教学赏析】

从知识的内在逻辑来看，平行和垂直是平面几何主要研究的两条直线的位置关系。现行大部分教材的设计都是将它们分开教学的。上述教学片段中，林老师将两者整合了起来，从分类的角度整体认知，避免学生“只见树木，不见森林”。从分类开始，建立“两条直线的位置关系”这一上位概念，为学习“垂直”和“平行”这些派生类属提供支撑，符合教育心理学中“渐进分化”的原则：“学习者在接触一个陌生的知识领域时，从已知的较一般的整体中分化较特殊的细节要比从已知的细节中概括整体容易一些。”此外，通过出示第二条直线，自然地将研究对象从一条直线引向两条直线;同时让第二条直线顺时针转动，顺势得到相交（含垂直）和平行的位置关系。这种不确定的关系，又为学生的思考留下了开放的空间，为直观想象素养的形成制造了契机。

从学生的学习困难来看，认识平面内两条直线的位置关系时，绝大部分学生对明显相交或平行的情况能够辨别，但是对看起来没有相交而延长后可以相交的情况存在较大争议。因此，林老师先通过对四组直线的分类，揭示相交和平行的概念;再出示一组看起来没有相交而延长后可以相交的直线，让学生辨别。这样的处理，一方面能使学生从整体上认识两条直线的主要位置关系是相交和平行，而不是垂直和平行;另一方面便于学生利用已经建立起来的相交和平行的概念去判断，从而深化对直线特征的认识，丰富相交概念的外延。

二、认识平行：从学习的浅表处追问

【教学片段】

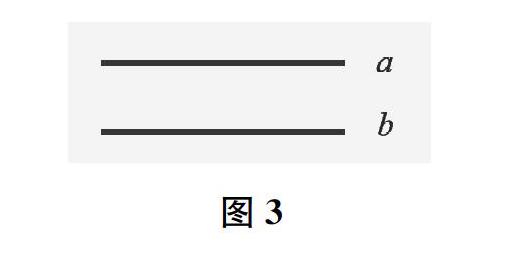
师（出示图3）为了便于叙述，我们把同一个平面内不相交的两条直线分别记作直线a和直线b。直线a与直线b互相平行，既可以说直线a是直线b的平行线，也可以说——

生直线b是直线a的平行线。

师“直线a是直线b的平行线，直线b是直线a的平行线”合成一句话就是——

生（众）直线a与直线b互相平行。

师（将一组平行线依次平移、旋转、缩短、离远，如图4）这两条直线还互相平行吗？

生（众）平行。

师为什么这两条直线始终互相平行？

生因为它们延长后不会相交。

师那为什么这两条直线延长后也不会相交？

（学生思考，不得其解。教师先出示两组平行线，再加上方格背景，如图5。）

生（恍然大悟，激动地指着左边一组平行线）这两条平行线左边、中间、右边都一样宽。

师这两条平行线左边相距几格？中间、右边呢？

生都相距两格。

师（把一条平行线向下平移一格）现在呢？

生都相距三格。

師左边这一组平行线可以看作一条直线向下平移两格或三格得到的。那右边这一组呢？

生可以看作一条直线向右平移两格得到的。

师现在你知道为什么两条平行线延长后不会相交了吗？

生两条平行线之间的宽度是一样的。

【教学赏析】

学习几何概念，不仅要认识概念的标准图形，而且要识别概念的变式图形。上述教学片段中，林老师将一组平行线依次平移、旋转、缩短、离远，让学生认识平行线的各种变化。如果说平行线的变化只触及概念的外在形式，那么“为什么这两条直线延长后也不会相交？”的追问则击中了概念的内在本质。这也正是学生思考不深的地方。在学生“愤悱”之时，林老师伸出援助之手，给平行线加上方格背景，为学生提供思维发展的“脚手架”。这样，学生对平行线的概念，就既可以理解为两条直线之间的“宽度”一样（即平行线之间的距离处处相等），又可以理解为一条直线是另一条直线平移后形成的。如此，就把两条直线永不相交的根源讲清晰、讲透彻、讲全面、讲深刻了。

三、认识垂直：从学习的疑惑处澄清

【教学片段】

师（出示图6）这两组直线都是相交的，有什么不同？

生右边的两条直线相交成直角了。

师是吗？怎么验证？

生用三角尺上的直角去比一比。

师（课件演示用三角尺的直角去比较，然后指着右边一组直线）两条直线相交成直角时，这两条直线互相垂直，其中一条直线是另一条直线的垂线，这两条直线的交点叫作垂足。（稍停）左边这一组直线互相垂直吗？为什么？

生左边这一组直线不互相垂直，因为它们没有相交成直角。

师直线a与直线b互相垂直，我们可以怎么说？

生（众）直线a是直线b的垂线，直线b是直线a的垂线。

师这两句话合成一句就是——

生（众）直线a与直线b互相垂直。

师你能把一张正方形的纸折两次，使两条折痕互相垂直吗？

（学生活动后展示两种典型的折法：沿对边中点连线折、沿对角线折。）

师大多数同学没有想到沿对角线折的方法，请大家再操作一次。

（学生活动。）

师（出示一组垂线，然后依次延长、缩短一条直线）这两条直线还互相垂直吗？

生（众）垂直。

师（分开两条直线）现在呢？

生（众）垂直。

师（整体平移、旋转两条直线）现在呢？

生（众）还互相垂直。

师为什么它們始终互相垂直？

生（众）因为它们相交成直角。

师（旋转一条直线，最终呈现图7）现在这两条直线还互相垂直吗？

生（众）不互相垂直了，不成直角了。

掌握概念，不仅要把握其相关特征（本质属性），而且要区分其无关特征（非本质属性）。垂直概念的本质属性是两条直线相交成直角，非本质属性包括两条直线画出来的

长短、是否相交、摆放位置等。上述教学片段中，林老师引导学生在变化对比中凸显垂直的本质属性，在操作体验中外化垂直的本质属性，在观察辨析中运用垂直的本质属性，帮助学生更好地建构垂直的概念：把握垂直的内涵，识别垂直的图形（尤其是“十”字形、“X”字形、“T”字形、“L”字形）。教学经验告诉我们，学生对垂直的认知远远低于对平行的认知。林老师深谙此理，在教学中投入了更多的时间，且针对学生的疑惑设计了比对、体验、辨析等活动，逐步帮助学生澄清关于垂直概念的疑惑。

四、沟通联系：从学习的混沌处完善

【教学片段】

师现在，我们知道了两条直线的位置关系有相交和平行。（用两根吸管演示）两条直线相交有1个交点。那么平行呢？

生（用两根吸管演示）没有交点。

师如果两条直线有无数个交点，那么这两条直线会怎样呢？请大家用两根吸管演示一下。

生（部分）完全重合。

师的确，重合也是两条直线的位置关系。不过，因为太特殊，所以数学上并不专门研究它。那么，重合、相交、平行之间有联系吗？用两根吸管比画比画。

生重合的两根吸管，把其中一根转一下就相交了。

师这里的“转一下”，用数学语言表达就是——

生旋转。

生重合的两根吸管，把其中一根移一下就平行了。

师这里的“移一下”，准确地说就是——

生平移。

（教师课件演示：在方格图中，旋转重合的两条直线中的一条成相交、垂直、相交，平移重合的两条直线中的一条成平行，如图8。）

师那么，两条直线的位置关系分成几类呢？

生三类。

生四类。

师究竟分成几类？谁来说说理由？

生我认为两条直线的位置关系分成相交、平行和重合三类，因为垂直只是相交的一种特殊情况，不能算作单独一类。

生（恍然大悟）喔！

师今天我们主要研究了其中哪两类？

生平行和相交。

生平行和相交中的垂直。

师你说得更加到位了，了不起！