三角形解的个数与正余弦定理

张茜茜

【基金项目】本文章为黑龙江省重点科研课题《高中生数学核心素养培养策略研究》（XHZ135-123）的研究成果.

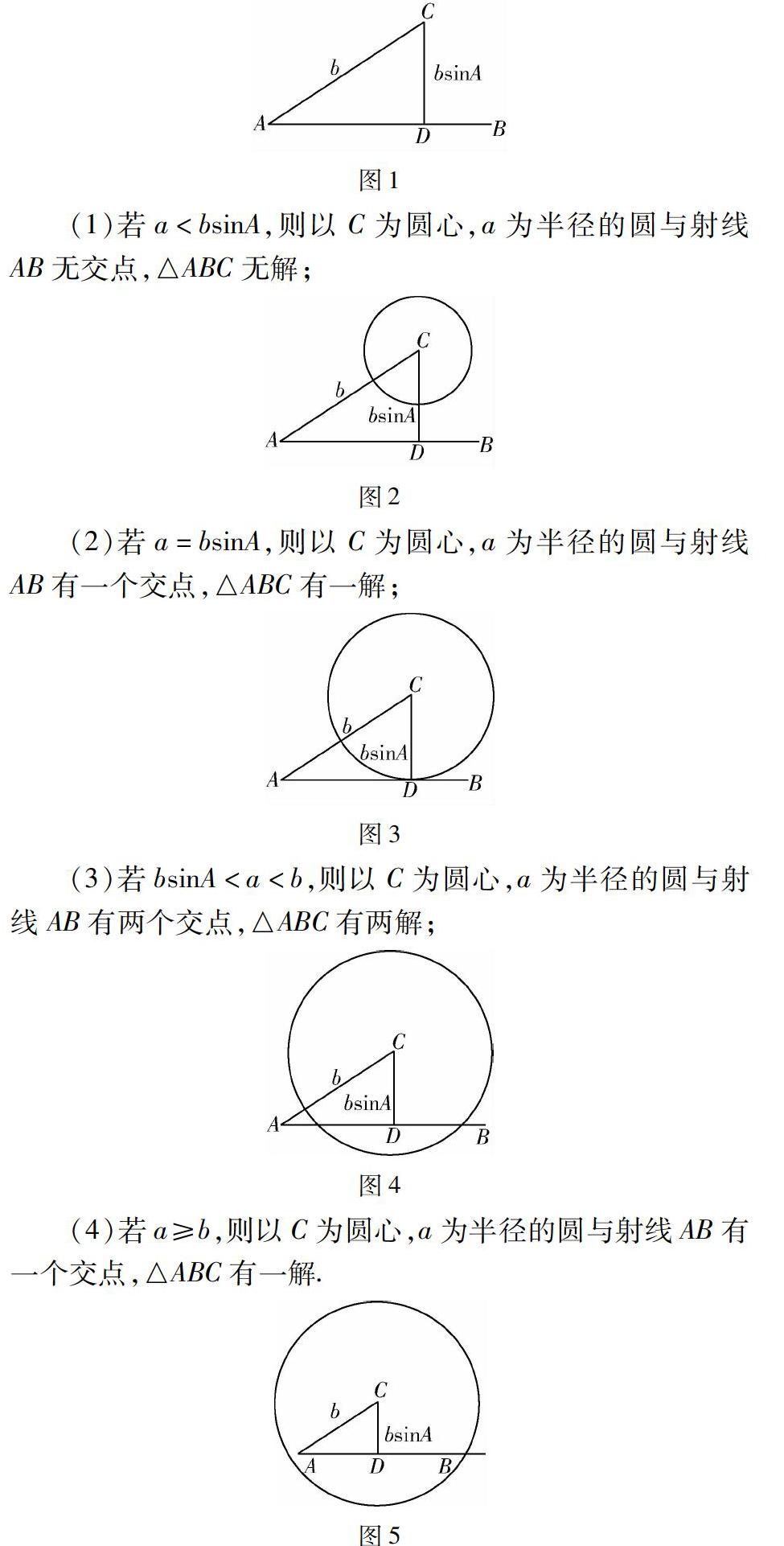
例在△ABC中，角A，B，C所对的邊分别为a，b，c，已知a，b，A（A为锐角），讨论三角形解的个数.

一、从正弦定理看多解取舍——数形结合解释

解法1如图1所示，过C点作CD⊥AB，垂足为D.

（1）若a

（2）若a=bsinA，则以C为圆心，a为半径的圆与射线AB有一个交点，△ABC有一解;

（3）若bsinA

（4）若a≥b，则以C为圆心，a为半径的圆与射线AB有一个交点，△ABC有一解.

二、从正弦定理看多解取舍——代数解释

解法2在△ABC中，由正弦定理可得asinA=bsinB，可得sinB.

（1）若sinB>1则无解，对应图2;

（2）若sinB=1则有1解，对应图3;

（3）若0sinA，则有2解，对应图4;

（4）若0

三、从余弦定理看多解取舍——正余弦定理的联系

解法3在△ABC中，由余弦定理可得cosA=b2+c2-a22bc，此时三角形解的个数由c的个数决定，即等价于函数f（x）=x2-2bcosA+b2-a2的零点个数.Δ=4b2cos2A-4（b2-a2）=4a2-4b2sin2A.

（1）当方程f（x）=0无解时，Δ<0，即a

（2）当方程f（x）=0有一解时为bcosA，此时Δ=0，即a=bsinA，对应图3的情形;所以方程有一解，则三角形有一解;

（3）当方程f（x）=0有两不等正根时，Δ>0且x1+x2=2bcosA>0，x1x2=b2-a2>0， 即bsinA

（4）当方程f（x）=0有一个正根，有一个非正根时，Δ>0且x1+x2=2bcosA>0，x1x2=b2-a2≤0， 即a≥b时，对应图5，所以正根可以作为△ABC的c边，此时三角形有一解;

（5）由于x1+x2=2bcosA>0，故方程f（x）=0不存在两根都非正的情形.

在已知条件为两边及一边对角（锐角）的情况下如何判断△ABC解的个数，多解情况出现的时候应该如何取舍一直是学生学习的难点，本文结合韦达定理分析了用余弦定理解三角形时应该如何取舍，同时将用余弦定理解三角形与图形一一对应.本文的研究成果应用于教学中，有助于培养学生的“数学抽象”“逻辑推理”核心素养.