基于爬山算法及微分进化算法的深孔轴线直线度误差评定
司欣格,包建东
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.南京理工大学 自动化学院,江苏 南京 210094)
0 引 言
根据形状误差的国家标准及国际标准,直线度误差定义为被测实际直线相对于理想直线的偏差,该理想直线应符合最小条件[1].直线度的优劣会影响产品的性能及寿命等指标,特别对于炮管,因此直线度误差的评判是一个重要的课题.已经有不少学者对于计算直线度误差作了很多工作.目前,深孔轴线直线度误差评定的方法也有很多.本文新研究了两种算法——爬山法和微分进化法来计算深孔轴线直线度误差.对这两种算法计算深孔轴线直线度误差过程进行仿真并对其结果进行评定.
1 评定方法
利用爬山算法和微分进化算法搜索理想直线得到直线度,并和其他算法比较其优劣性.采用实验中得到的不同坐标的偏心距进行仿真实验.
1.1 目标函数的确立
目标函数的确立建立于最小包容区域法[2].
假设直线方程
f(x)=kx+b.
(1)
与包容直线平行.
xi,yi为测量得到的数据
计算各点到直线(1)y轴方向的距离,即
εi=yi-f(xi).
(2)
求出εi中的最大值和最小值,令
g(x)=max(εi)-min(εi),i∈{1,2,3,…,10}.
(3)
满足g(x)最小的直线为理想直线,g(x)为目标函数,得到的值越小,越满足条件[3].又有
g(x)=max(εi)-min(εi)=
max(yi-f(xi))-min(yi-f(xi))=
max[yi-(kxi+b)]-min[yi-(kxi+b)]=
max(yi-kxi)-min(yi-kxi).
(4)
所以目标函数ε(x)和直线截距b无关.
1.2 爬山算法
即g(kc)与g(kc+length),g(kc-length)进行比较,(kc为当前位置).并向最优的方向前进一步,否则当前位置即为最优解位置.
爬山算法的优点是避免遍历,从某点判断前进的最优方向来搜索出一条能够达到最优解的路径[4].
归一化[5],令
k=kmin+kc(kmax-kmin).
(5)
1.3 微分进化算法
微分进化算法相比遗传算法最大的优势就在于能够保留优秀的变异个体[6].操作如下[7]:
1.3.1 变异操作
vi=xr1+F(xr2-xr3),i=1,2,…,NP,
(6)
式中:{xr1,xr2,xr3}是在父代种群中随机选取的3个不同的个体,vi为变异后的个体,NP为种群规模,NP≥4,F∈[0,2](常量).
1.3.2 交叉操作
ui=[ui,1,ui,2,…,ui,D]:
i=1,…,NP,j=1,…,NP,
(7)
式中:randb∈[0,1](随机数);CR∈[0,1](常量);randj∈[1,D](随机数).
1.1.3 选择操作
(8)
本文使用的优化算法基于搜索理想直线.
利用式(4)对KC进行归一化,对归一化的KC进行二进制编码,将随机得到的向量KC当作个体,对其进行微分进化.
2 仿 真
实验数据来自文献[8],通过光电测试对深孔不同位置的偏心距进行测量,得到表1 数据.
2.1 爬山算法仿真参数
爬山算法实验参数如表2所示.

表2 爬山算法实验参数表
2.2 微分进化算法仿真参数
微分进化算法实验参数如表3所示.

表3 微分进化算法实验参数表
2.3 仿真结果分析
从表4 结果可以看出,爬山算法3次实验得到的直线度误差虽然接近,但却不同,说明目标函数g(x)有很多极小点.这也暴露了爬山算法搜索直线度的问题——易陷入局部最优.解决的办法是采样随机重启爬山算法.除此以外,爬山算法搜索的次数较多,效率较低.
从图1 和表4 可以看出,微分进化算法不到20步就收敛到最优解,可以看出其效率之高,而且也能得到较为精确的值.图像也反映了微分进化算法只保留优秀的个体.但在实验过程中,偶尔也会陷入局部最优,得到一个较大的值.解决的办法是对微分进化算法变异策略进行改进,如文献[9]的方法,增加跳出局部最优的几率.
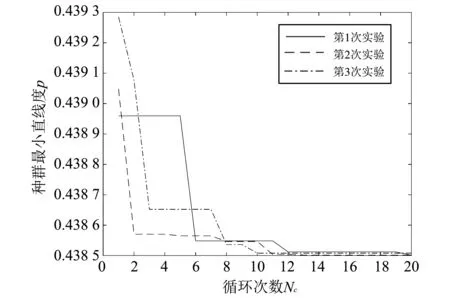
图1 微分进化算法进化过程
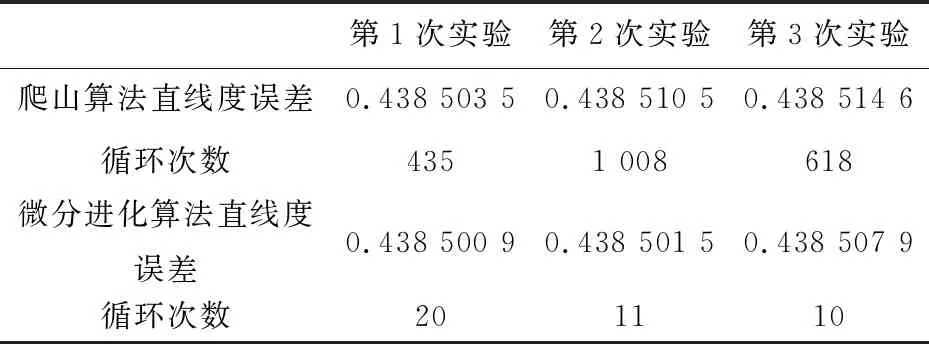
表4 仿真结果
3 结果比对

表5 各算法计算结果

表6 结果比较
本文仿真结果与文献[8]结果比对可知,爬山算法和微分进化算法得到的精度都高于极值搜索法和分割逼近法.微分进化算法得到的精度是最高的.
4 结 论
通过仿真实验可知,使用爬山算法和微分进化算法计算深轴孔直线度都是可行的,而且能得到较高精度的值且具有较高的效率,爬山算法的效率要低于微分进化算法.但是,针对两种算法都有可能陷入局部最优解的情况,还需要利用已有的方法对算法进行改进.

