材料塑性损伤的共轴异向波束混频定位及表征方法

王浩坤，何军榜，王召巴

(1.中北大学 信息与通信工程学院，山西 太原 030051；2.中国石油集团西部钻探井下作业公司，新疆 克拉玛依 834000)

0 引 言

金属材料在工作过程中由于受到应力和环境的作用，不可避免地会产生塑性变形.过度的塑性变形会降低金属的延展性并给结构带来早期的疲劳损伤[1].在大多数的试验中，能够表征金属材料疲劳损伤和塑性应变的可测量参数是超声非线性参数β[2].

目前测量超声非线性参数使用最广泛的方法是二次谐波法.该方法将一束特定频率的基波脉冲(纵波、瑞利表面波或者兰姆波)通过超声波换能器射入待测材料中，入射声波与材料非线性相互作用生成相应的二次谐波.二次谐波幅值和基波幅值平方的比值正比于超声非线性参数βL，通过测量二次谐波和基波的幅值即可获得待测材料的超声非线性参数βL.虽然二次谐波法的理论简单且便于施行，但其有两个缺点：① 二次谐波法测得的超声非线性参数βL是发射换能器与接收换能器之间的平均值，该方法测量βL的空间分辨率是有限的.② 二次谐波法测得的非线性并非全部由材料非线性引起，其中包含了测量系统本身带有的非线性，降低了该方法的准确性[3].

为了克服二次谐波法的局限，科学家[4-5]建立了共线波束混频法来测量金属材料的疲劳损伤和塑性应变.共线波束混频法对塑性变形[6-7]、晶界间腐蚀[8]和微裂纹[9-10]等比较敏感.同时它可以扫描棒状试样以确定声学非线性参数延轴向分布的情况.当入射纵波和入射横波满足频率匹配的条件时，两激励波共线相互作用将产生第3束共振波.共振波的幅值与超声非线性参数βT成正比，通过测量共振波的幅值即可获得待测材料的超声非线性参数βT.共线混频方法可以自由选择混频波的频率，能够排除由测量系统的非线性引起的高次谐波的影响[11].

本文基于共轴异向波束混频方法实现了对试样塑性变形区的定位及表征.具体研究了激励脉冲频率的确定、激励脉冲时延的确定以及声学非线性参数与材料塑性变形之间的关系.

1 共轴异向混频的解析解

在二维笛卡尔坐标系xy中，假如一束平面波在x轴方向传播，那么它的质点运动方程是x和t的函数.平面波在x轴方向和y轴方向上的位移分别表示为u(x,t)和v(x,t)，平面波的波动方程表示为

(1)

(2)

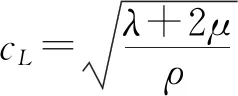
(3)

式中：λ和μ是拉梅参数；m和n是三阶弹性常数；βL和βT是无量纲超声非线性参数.

假如一束剪切波u1在y轴正方向传播，而另一束纵波v1在y轴负方向传播，则有关系式

(4)

(5)

如果这两束激励脉冲的频率满足

(6)

则将产生一束沿y轴负方向传播的共振剪切波u2，u2的表达式为

(7)

(8)

(9)

这里忽略了非共振高阶波的影响.只要测量出共振剪切波u2的幅值A，即可通过式(10)求出材料的非线性参数

(10)

式中：lm表示两束激励波在试件中相互作用的区域.

2 试样的制备

大量的实验研究表明，金属材料的塑性变形量和声学非线性参数之间呈增长关系，具有不均一塑性变形的试样即含有分布不均一的声学非线性参数.

本文所使用的试件为LY12铝合金漏斗形试件，其几何尺寸和样品分别如图1 和图2所示.试件的具体参数如表1所示.在机加工之前，原材料的声学非线性参数已被测量，排除了材料自身声学非线性参数分布不均带来的影响.漏斗形试件被单向轴向力拉伸到屈服强度之上，试件2，3，4平行段部分的塑性应变分别为1.4%,2.8%和4.4%.将该漏斗形试件加工成圆柱形试件，加工后的圆柱形试件如图3所示.查阅相关资料可以发现，塑性变形主要集中在试样的平行段Lm.

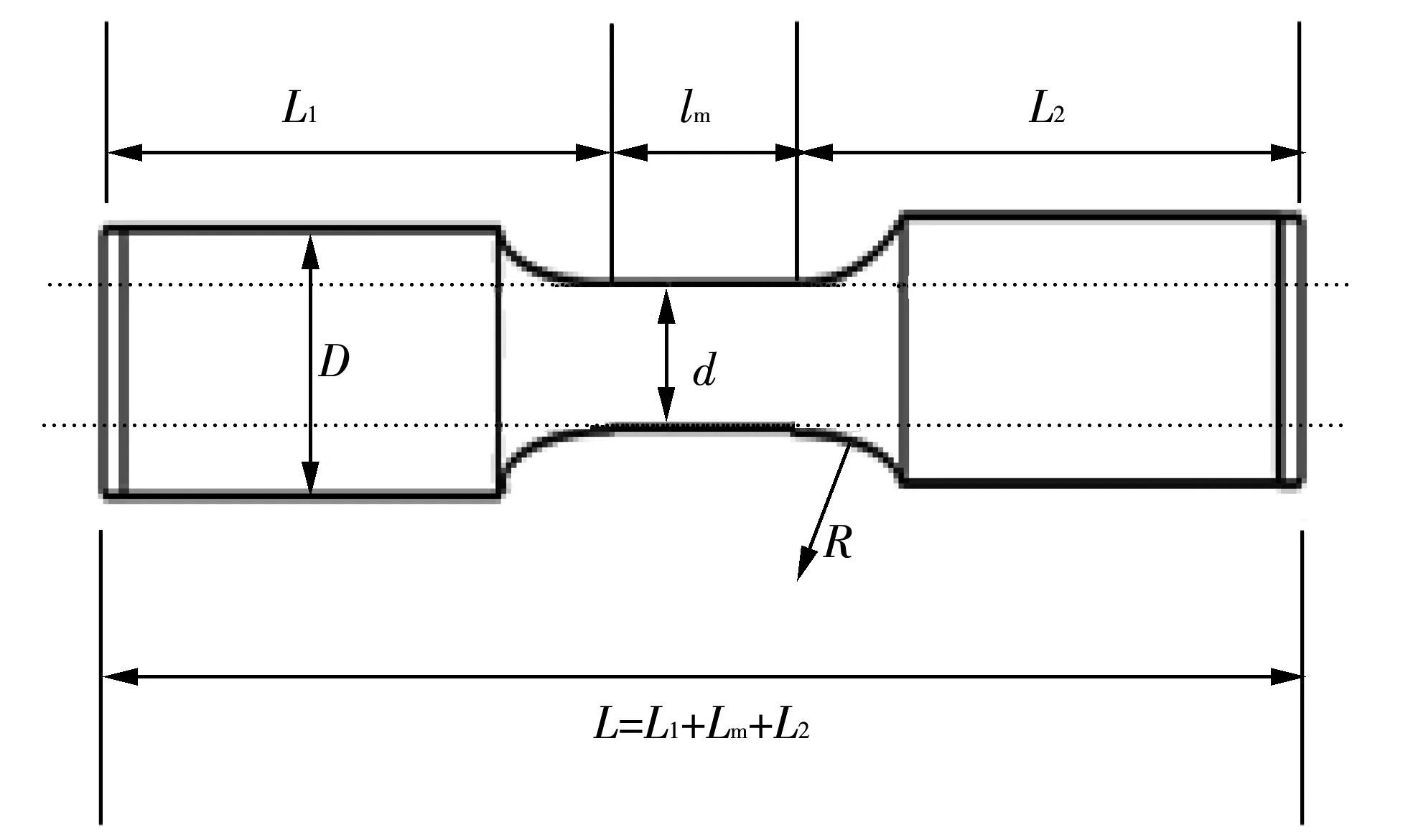
图1 试件的几何尺寸

图2 漏斗形试件样品

图3 圆柱形试件样品

表1 漏斗形试件的具体参数

3 实 验

3.1 实验装置

本文搭建了共轴同向混频非线性超声检测系统.实验装置和实验平台分别如图4 和图5所示.非线性高能超声系统RAM-5000 SNAP作为信号发生器，系统内部的触发器作为参考触发器.频率为5 MHz的宽带剪切波换能器和频率为10 MHz的窄带纵波换能器分别连接到RAM-5000 SNAP的1通道和2通道.RDX-6双工器与剪切波换能器相连，使得剪切波换能器能同时作为发射换能器和接收换能器工作.两激励脉冲波相互作用生成的混频波被剪切波换能器接收，传送给与RAM-5000 SNAP系统相连的数字示波器，示波器数字化的时域信号被发送到电脑上进行后置信号处理.

图4 实验装置

图5 实验平台

3.2 激励频率的设置

如第1节所述，激励纵波和激励剪切波的频率需要满足共振波产生的充要条件式(6).为了设置两激励脉冲的频率，需要精确测量激励纵波和激励剪切波在试件中的波速.本节中采用脉冲回波法分别测量到该漏斗形试件中激励纵波的速度为6 386 m/s，激励剪切波的速度为3 093 m/s.波速测量如图6所示.

根据测得的纵波波速、剪切波波速以及共振剪切波产生的充要条件求得

设置激励剪切波的频率为2.50 MHz，则激励纵波的频率为9.70 MHz，共振波的频率为7.20 MHz.

图6 漏斗形试件中纵波和剪切波波速的测量

3.3 激励脉冲时延的设置

通过调整两激励脉冲的时延，可以使两激励主波在试件中的不同位置混合，从而获得试件不同位置的超声非线性参数和塑性应变分布.两激励主波和共振波在试件中的传播路径如图7所示.

图7 激励主波和共振波在试件中的传播路径

假设两激励主波在距离试件左端Xmm距离处混合.则可以计算出激励剪切波从激发到传播X距离处时间为

纵波从激发到传播到X距离处的时间为

两激励主波的传播时间差TS-TL(假设TS-TL>0)即为激励脉冲的时延差.若激励剪切波的时延为t1,则激励纵波的时延为t1+(TS-TL).

3.4 实验方法

实验时按照图5所示连接好实验装置.纵波换能器和剪切波换能器分别耦合在圆柱形试件的两侧，两换能器的耦合位置要严格对齐，其中剪切波换能器用专用横波耦合剂或者蜂蜜耦合，纵波换能器用医用超声耦合剂耦合.连接好实验装置后，操作软件设置纵波换能器的激发频率为9.70 MHz，脉冲长度为14个周期，初始相位设置为0°；剪切波换能器的激发频率为2.50 MHz，脉冲长度为14个周期，初始相位设置为0°.设置两个激励波的时延使其在试件中心处的应力集中区相遇产生第3束共振波，共振波沿着与剪切波传播相反的方向传播，被剪切波换能器接收.理论计算得到共振波频率为9.70-2.50=7.20 MHz，共振波出现的时间为T，

T=T(剪切波)+T(共振波)+T(延时)=

将示波器上62 μs开始的信号保存至U盘；其他条件保持不变，将剪切波的和纵波的初始相位设置为180°后再次进行实验，将示波器上62 μs开始的信号保存至U盘.在计算机上进行后续处理，通过Matlab程序将两次实验的数据相加除以2后便得到共振波的时域波形，如图8所示.

图8 共振波的时域波形

对图8所示的共振波时域信号进行快速傅里叶变换(FFT)，得到的共振波的频域图，如图9所示.

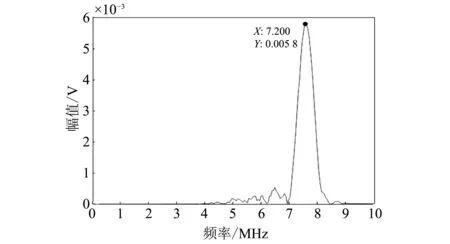
图9 共振波的频域波形

4 实验结果与分析

从图8 可以看出共振波的波形是严格的菱形，且共振波的出现时间为62.4 μs左右，与理论计算一致；从图9可以看出共振波的频率是7.20 MHz，与激励纵波和激励剪切波的频率之差一致.将从图8 得到的共振波幅值A代入式(10)即可求得待测铝合金试件的非线性参数βT，从而得到试件在该位置的塑性损伤.

通过操作软件控制激励纵波和激励横波的时延，使得两激励主波在圆柱形试件的不同区域相遇，即可测量棒形试件不同位置的非线性参数βT.本文取4个试件在中间处混频产生的共振波来表征材料的非线性.试样1，2，3，4的声学非线性参数将进行归一化处理，求得βTi/βT1，其中βTi表示第i个试件的声学非线性参数，βT1表示未发生塑性变形区域的声学非线性参数.声学非线性参数与塑性变形量之间的关系如图10所示.由图10 可知：随着塑性变形的增加，声学非线性参数呈现增长趋势.

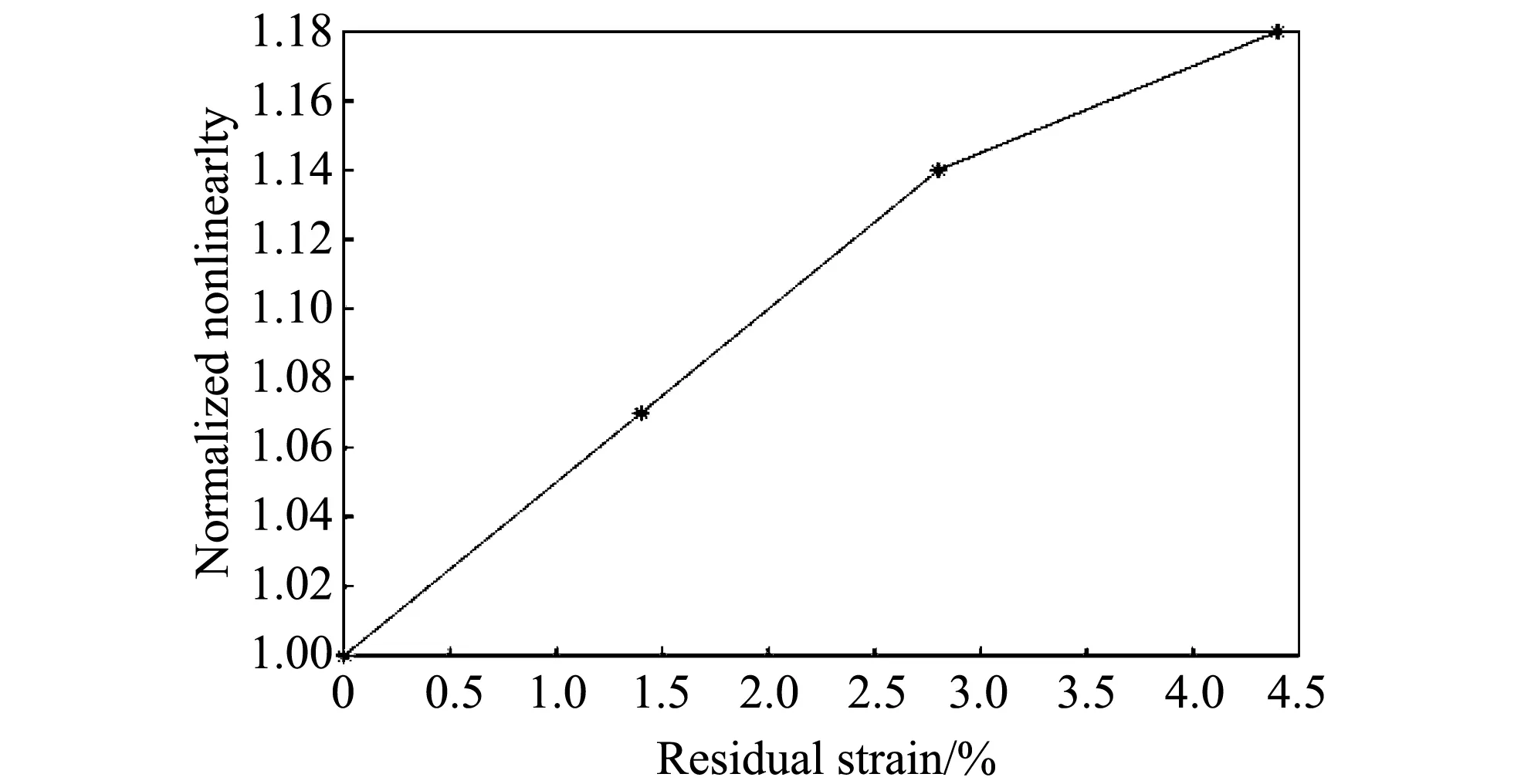
图10 声学非线性参数随塑性应变的变化

5 结 论

本文提出采用共轴异向混频方法无损检测铝合金试件的非线性参数βT，从而实现材料塑性损伤的定位和表征.实验结果表明，共轴异向混频检测方法对金属材料的塑性变形比较敏感，可以检测出材料早期的塑性损伤.通过操作软件控制激励纵波和激励横波的时延，使得两激励主波在圆柱形试件的不同位置相遇，即可检测试件不同位置的塑性损伤.随着塑性变形量的增加，声学非线性参数也呈增长趋势.