基于DL-MPWFRFT卫星混沌加密通信研究

王浩波，达新宇，倪 磊，潘 钰

(1.空军工程大学研究生院，陕西西安 710077；2.空军工程大学信息与导航学院，陕西 西安 710077)

卫星通信具有通信范围广阔、成本低、受地理位置影响小和通信带宽高等优点［1］。但卫星通信信道开放，发送的消息会被第三方拦截共享，对我方通信造成干扰和破坏；易受信道中种种干扰的影响；同时卫星通信传播需要经过较远的路程，信息到达地面会有衰减。因此如何使卫星通信的抗截获性、保密性能力更强，就显得尤为重要［2］。

目前的卫星抗截获手段主要集中在跳频、扩频和人工噪声［3］等方面，但这些方式抗截获性能不强，依赖于信道的状态信息，实际应用会受到很大的限制。作为信号处理技术代表的加权类分数阶傅里叶变换［4］(Weighted-type Fractional Fourier Transform，WFRFT)已广泛应用于光学、量子力学［5］方面。文献［6］定义了WFRFT的离散形式，使其适用于数字通信，并且提出了数字通信系统方案。经过WFRFT变换处理，信号的星座图发生了旋转和扩散，文献［6］利用此特点提出保密和抗截获通信应用的可能性。文献［7］在文献［6］的基础之上，进一步分析了WFRFT的抗截获性和分裂特性。由于单参数WFRFT方案变量单一，所以通信抗截获性能有限。针对此问题，文献［8］提出双层多项多参数加权类分数阶傅里叶变换(Double Layers Multi-parameter Weighted-type Fractional Fourier Transform，DL-MPWFRFT)的隐蔽通信方案，通过增加变换层数，使变换的复杂度进一步增加，加大了隐蔽通信的抗截获性，但当阶数较小时仍存在抗截获能力不强的瑕疵。

针对上述问题，本文提出一种基于DL-MPWFRFT的混沌相位加密调制方案。在DL-MPWFRFT变换的基础之上，对信号进行Logistic混沌相位加密，利用混沌序列的随机性改变信号的星座图特性，进一步隐藏变换参数，从而实现在任意阶数下的信息传输的安全性，使抗截获能力大幅提升。

1 双层多参数加权类分数阶傅里叶变换

1.1 MPWFRFT变换

采用归一化的离散傅里叶变换(Discrete Fourier Transform，DFT)定义为：

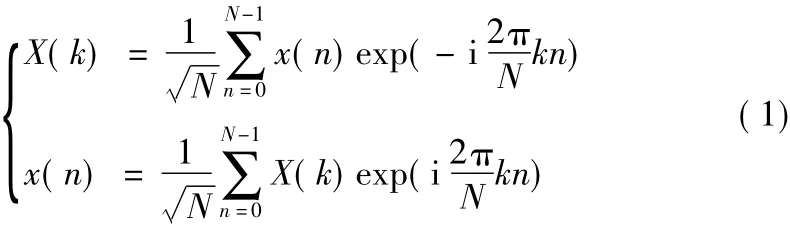
式中，N为DFT变换的区间长度；n为时域离散的点；k为其对应频域的频率大小。DFT的矩阵形式为

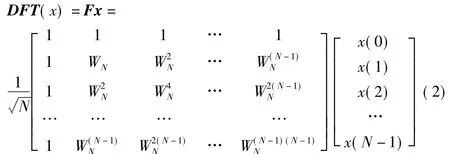
式中，矢量 x=［x(0)，x(1)，…，x(N-1)］T，N 是矢量序列x的长度，WN=exp(-i2π/N)，F是DFT变换矩阵。

令X0=x为原始离散序列，X1，X2，X3分别是X0的一、二、三次DFT变换，则多参数加权分数阶傅里叶变换定义为［9］：

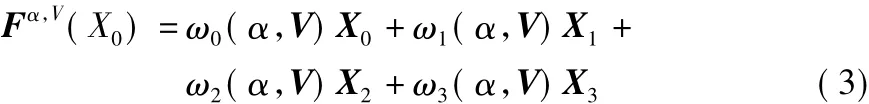
其加权系数定义为

式(3)中，α 表示变换阶数，V=［MV，NV］=［m0，m1，m2，m3，n0，n1，n2，n3］是尺度向量，总共有 9 个参数。故离散序列的多参数加权类分数阶傅里叶变换(Multiparameter Weighted-type Fractional Fourier Transform，MPWFRFT)可以表示为

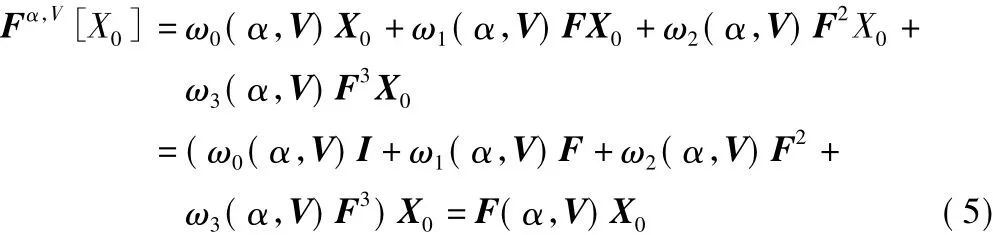
其中，F(α，V)表示MPWFRFT变换矩阵。

进一步，DFT采用式(2)所示能量归一化的定义表示，推广利用矩阵表达得到如下形式：

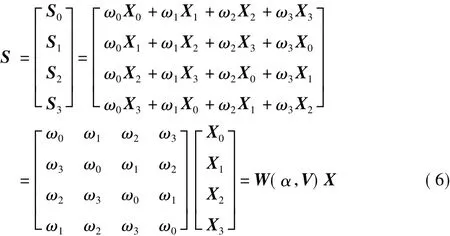
式中，S0，S1，S2，S3分别表示 X0的 0 ～3 次 MPWFRFT；W(α，V)表示MPWFRFT变换的系数矩阵。并且可以利用参数为-α，V的MPWFRFT实现逆变换

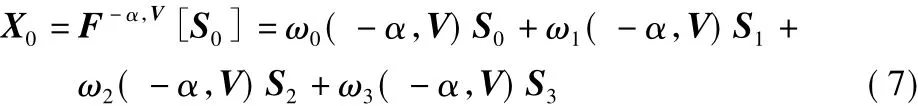
1.2 DL-MPWFRFT变换

DL-MPWFRFT变换实际上是先将调制过后的信号分成两部分，这两部分长度可以相同也可以不相同。将两部分信号各自进行MPWFRFT变换，然后将变换过后的信号连接在一起再进行一次MPWFRFT变换。具体原理图如图1所示，此图中两部分信号长度相等。图2所示为反变换示意图，将各个MPWFRFT变换的阶数取反，进行相应长度的反变换，最后可以得到原数据。由于增加了变换的层数，使得变换参数变得更加复杂，并且长度参数也可调，就进一步增加了第三方截获信息的可能性。

图1 DL-MPWFRFT变换示意图

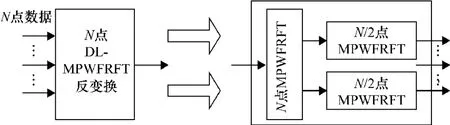
图2 DL-MPWFRFT反变换示意图

从图1中知道第一层MPWFRFT变换的数据长度为N/2，设两个部分信号为g(n)，x(n)，则根据MPWFRFT变换的定义可得：

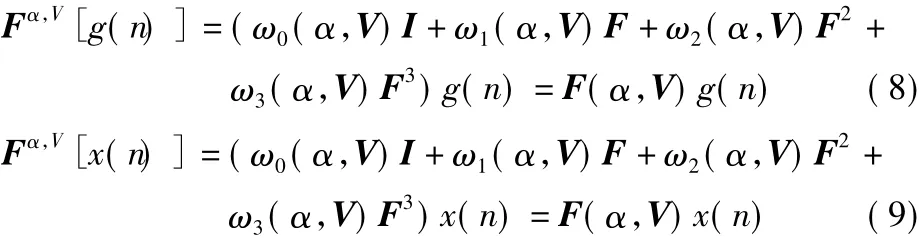
其中，V表示第一层变换参数。

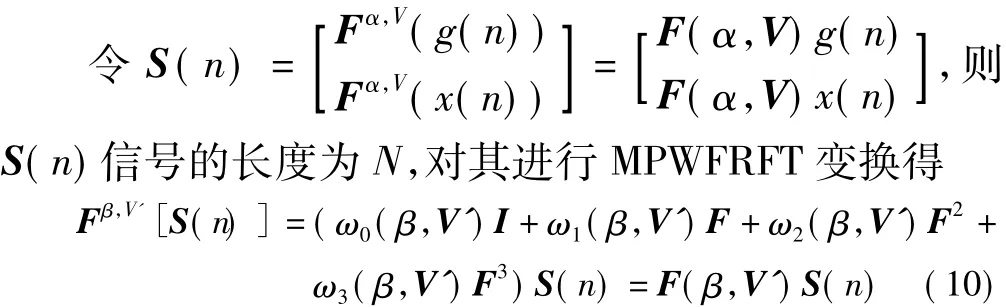
将S(n)代入式(10)中得到DL-MPWFRFT变换的表达式为

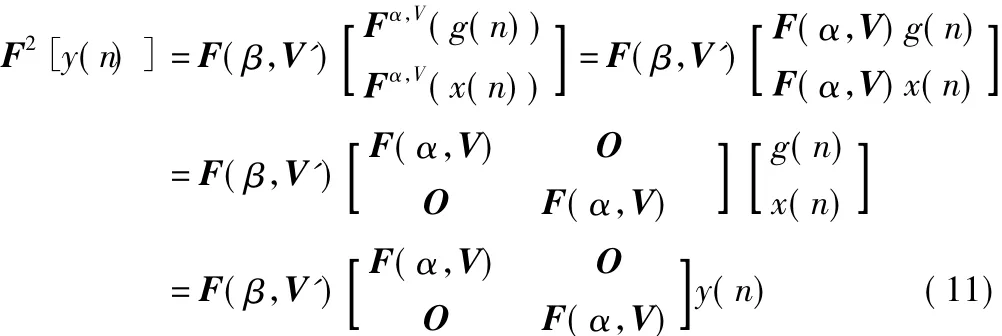
式中，F2表示DL-MPWFRFT变换矩阵；y(n)表示原始的数据信号；V'表示第二层变换参数。同理对DL-MPWFRFT信号进行(-β，V'，-α，V)的 MPWFRFT 变换即可得到初始信号。

2 Logistic混沌扰乱及其卫星通信系统

2.1 Logistic混沌映射相位

Logistic混沌映射具有复杂的运动特性，其产生的数据具有良好的随机性，故在保密业务中得到了大量的应用。目前用来产生混沌随机序列的常用映射主要有一维Logistic映射、改进Logistic映射、Chebyshev映射，而由于一维Logistic映射结构简单，性能良好，在实际应用中得到了大量的应用。其表达式为［10］

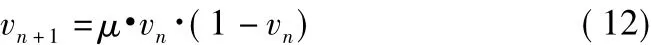
式中，μ为分形系数，取值范围为μ∈(0，4］；vn为混沌映射输出值，其取值范围为 vn∈(0，1)；n=0，1，…，为迭代次数。研究表明，当初始值v0取值在0，1之间，分形系数3．57＜μ＜4时，经过一定次数的运算，序列将进入混沌状态，同时初始值的取值对生成序列有着直接的影响。

将产生的序列作用于相位，混沌相位数学表达式为

经过正交相移键控(Quadrature Phase Shift Keying，QPSK)映射的基带信号通过DL-MPWFRFT加密处理，然后将加密数据与混沌相位相乘，得到扰码后的加密信号，具体实现如图3所示。

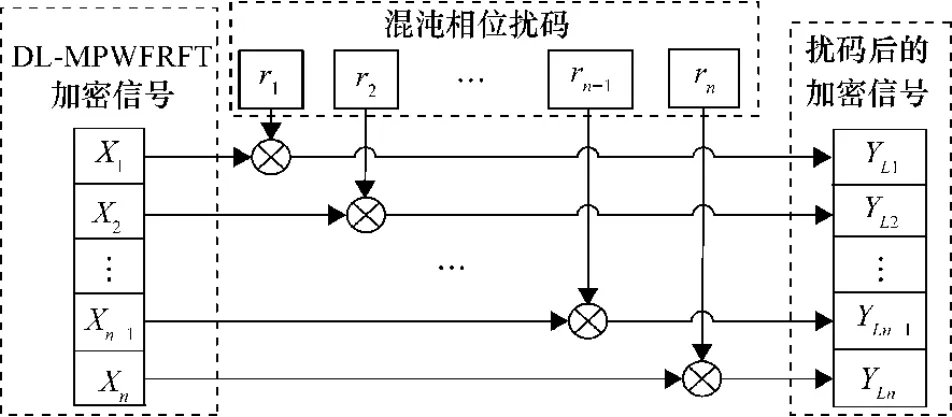
图3 混沌相位扰码示意图

假设传输信道是高斯白噪声信道，表示为n0，经过DL-MPWFRFT处理之后的信息为Xn，则接收信号表示为

接收端的信号首先进行混沌相位解调，将式(13)中的vn取负值，得到

则相位解调过程为

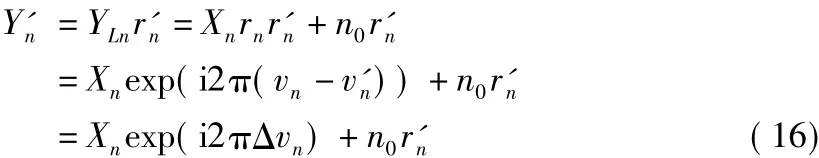
式中，Y'n为正确解调相位之后的信号，由于r'n符合在［0，1］之间的均匀分布，与高斯白噪声密度n0相乘之后，只需要直接进行滤波处理就可以消除。故正确解调相位的关键只与Δvn的取值大小有关。对于目的接收机，由于收发双方事先知道相关的参数，故当正确取值初始值v0时，接收方可以产生和发方相同的混沌序列，故Δvn=0，可以得到正确解调的信号。对于非目的接受机，由于事先不知道相关参数，故不能保证Δvn=0，所以得不到发送的信息，从而实现加密通信。

2.2 DL-MPWFRFT混沌扰码卫星通信系统

由于隐蔽信号具有类高斯性，故将隐蔽信号搭载在原有的卫星业务信道之上，实现重叠卫星通信。如图4所示。

数据源进行加密之后，通过QPSK基带映射，然后进行串并转换。隐蔽信号经过DL-MPWFRFT变换和混沌相位扰码处理，与原有的卫星业务信号进行叠加传输，通过上行链路、卫星转发器以及下行链路被接受端捕获。通过滤波处理将隐蔽信息与原有的业务信息分离开来，并做相应的逆变换处理，从而得到传输的隐蔽信号。由于DL-MPWFRFT变换需要27个参数，混沌相位扰码需要初始参数值，故对于非目的接收机，在事先不知道合法参数的情况下，将隐蔽信号解调出来的可能性降低，从而达到隐蔽通信的目的。

3 系统性能分析

3.1 DL-MPWFRFT星座图特性仿真

将长度为1024的数据信号经过DL-MPWFRFT变换处理，信号星座图发生的变化如图5所示。

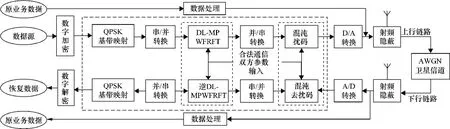
图4 DL-MPWFRFT混沌扰码卫星通信系统

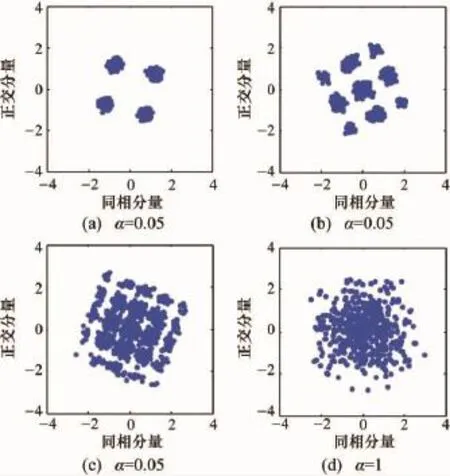
图5 DL-MPWFRFT星座图特性

表1所示为图5中DL-MPWFRFT变换的各层参数值，αi、Mi、Ni表示 DL-MPWFRFT 变换第 i层的具体变化参数，其中图5(a)、图5(b)、图5(c)的变换阶数较小，图5(d)的变换阶数较大。由图中可以看出，DLMPWFRFT增加了变换的参数个数，使得变换系统复杂度得到提高，非目的接收机截获信号的可能性变小。但当变换阶数较小时，信号仍没有充分旋转和扩散，非目的接收机仍有可能截获信号。

3.2 DL-MPWFRFT混沌相位星座图特性仿真

一维Logistic混沌映射分叉图由稳定不动点、不稳定不动点、周期和混沌4个状态组成。当参数μ取值在［0，1］之间，映射值在0处收敛；当参数μ取值在［1，3.57］之间时，映射值收敛于有限个数值；当参数μ取值在大于3.5699时，映射值进入混沌状态；当参数μ取值为4时，映射值达到完全混沌，混沌状态比较充分，且复杂度比较大。故进行仿真实验时，μ取值应为4，此时复杂度最高。为了使产生序列充分混沌，迭代次数取值在200次以上。

将经过DL-MPWFRFT处理的信号实施相位混沌扰码，其中Logistic的系数μ=4，初始值v0=0.9，所得信号的星座图特性如图6所示。

从图6中可以看出，图6(a)为QPSK信号经过混沌相位处理之后得到的星座图，在扰码因子的作用之下，信号将变得难以破译；当变换阶数较小时，展现出来的星座图特性如图6(b)所示，此时星座图开始扩散；当变换阶数α=1时，信号的星座图呈现类高斯分布，具有不规律性，非目的接收机无法再通过高阶累积量对信号进行破译，实现了隐蔽通信，对信息的安全传输提供了重要的保证。

3.3 误码率特性仿真

假设信号在信道中传输的长度为1024-bit，在MATLABR2014a实验平台之下，经过 DL-MPWFRFT混沌相位处理之后，非目的接收机进行截获。这里首先考虑Logistic混沌相位对解调误码率的影响，DL-MPWFRFT相关参数正确，仅在Logistic混沌相位初始值有误差。当初始值v0为0.9时，分别取初始值误差 Δv0为 10-1、10-5、10-10、10-15、10-20，将 v0+ Δv0作为Logistic初始值并对信号进行DL-MPWFRFT混沌相位处理，迭代200次，做出7种情况下的误码率相关特性图，如图7所示。

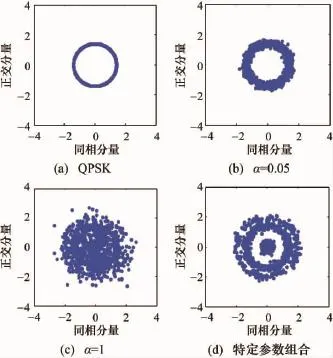
图6 DL-MPWFRFT混沌相位系统星座图

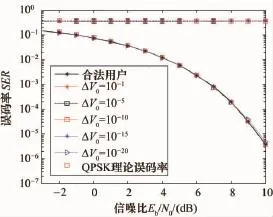
图7 使用不同初始值误差时对应的误码率

从图7中可以看出，当初始值误差Δv0分别为为10-1、10-5、10-10、10-15时，非目的接收机的误码率处于一个较高的水平；当初始值误差Δv0为10-20时，解调的误码率才和合法用户的误码率接近，所以仅仅在混沌相位这里系统抗扫描参数就提高了1020次，大大提升了系统的安全性。同时，合法用户的误码率和QPSK处理的误码率相近，从而表明采用此种方法不会给系统增加负担，从而提升了可靠性。

4 结束语

本文提出了一种基于DL-MPWFRFT的卫星混沌相位加密通信方法。首先介绍了MPWFRFT的相关概念，通过增加变换参数，提出了DL-MPWFRFT的变换方法，使信息安全传输的能力得到加强，抗截获性得到提高。为使隐蔽性能进一步提高，对处理之后的信号进行混沌相位加密，实现双重加密。通过仿真可以看出，加入混沌相位加密使得信号的星座图特性发生变化，抗扫描性能得到提高，非目的接收机截获信息的概率降低。同时，误码率也表明该方法不会增加系统负担，增加了系统正常工作可靠性。