救助船模拟器中Stewart摇摆台运动仿真

(1.大连海事大学 船舶机电装备研究所，辽宁 大连 116026；2.北京机械工业自动化研究所有限公司，北京 100120)

引言

海上事故发生时，常伴有大风大浪等恶劣天气。作为最有效地救援方式之一，常以出动救助船来实施海上救援[1]。实际的波浪更接近短峰不规则波，在这种恶劣的天气中，救助船会出现大幅度摇荡运动，横摇角有时甚至超过30°。为模拟救助船在真实海况中的动态响应，有必要在救助船操纵模拟器中，引入六自由度Stewart并联运动平台，对救助人员进行海况适应性训练[2-3]。

船舶操纵模拟器主要分为4个等级，即功能完备、多功能、有限功能和单一功能。功能完备的模拟器，其行为真实感要求具有六自由度运动功能，可通过船舶运动数学模型、视景系统和Stewart平台来实现。现有船舶模拟器的标准中，没有明确提出对Stewart平台模拟不同海况下船舶运动的相关技术要求[4-5]。 因此，本研究将船舶的运动与Stewart平台相结合，运用理论和仿真的方法实现Stewart平台模拟船舶运动，这为救助船模拟器的研究及相关标准制定，提供一种可靠有效的方法。

在Stewart平台运动仿真方面，为直观的分析机构在不同位姿下各液压缸伸缩量的变化，赵静一等[6]在MATLAB/Simulink中建立基于运动学反解算法的仿真模型，对Stewart平台的6个单自由度的液压缸运动进行仿真，通过仿真曲线可直接观察各液压缸活塞杆伸缩量的变化规律，但仍然是以二维曲线的形式来研究Stewart平台的运动。姜洪洲等[7]采用运动学反解算法，使用三维虚拟现实建模语言VRML-Java实现Stewart平台构件之间的约束和空间动态装配；将VRML的ActiveX控件嵌入到LabVIEW的用户界面中，实现与虚拟平台的数据通信和运动控制。之后姜洪洲等[8]又提出基于运动学分析的两种动态装配算法，即基于大地固定坐标系的动态虚拟装配算法和基于变换层级的动态虚拟装配算法，在Stewart平台控制和仿真总系统中，通过以太网与运动控制计算机和逻辑计算机组成的控制系统进行实时的信息共享，实现了在线运动仿真。但是，在上述研究中，没有对所提出的仿真方法进行试验验证。在使用液压摇摆台模拟波浪中的船舶运动方面，皮阳军等[9]利用Stewart平台复现随机海浪谱，对舰载设备进行振动模拟试验，为测试舰载设备在随机海浪环境中的性能和可靠性提供了一种方法，结果表明，Stewart平台能有效复现随机海浪谱，功率谱密度误差可控制在±1 dB以内。赵鸿博等[10]使用4个液压缸搭建了一种可仿真船舶横摇和纵摇的二自由度平台，采用模糊PID控制算法，有效的模拟了船舶在6级海况下的横摇运动。这方面，前者的研究仅利用Stewart平台对海浪谱进行了复现，而后者局限于利用二自由度平台来模拟船舶的横摇和纵摇运动。

综上所述，从理论和仿真的角度，将船舶的摇荡运动与Stewart平台运动复现两方面相结合。采用基于运动学分析和变换层级的动态装配算法，在Virtools Scripting Language(简称VSL)的编程环境中[11-12]，建立Stewart平台的数据驱动机制，并通过与试验的对比，验证了算法的正确性；以南海救111船在短峰不规则波中的横摇和纵摇运动作为输入信号，实现三维空间中Stewart平台的虚拟装配和可视化运动。

1 基于运动学分析的动态装配算法

六自由度Stewart并联运动平台的实物结构如图1所示。根据其运动特性，只对7个基本构件进行三维建模，包括上平台、上铰支座、上铰轴、活塞杆、液压缸、下铰轴和下铰支座，各构件及坐标系如图2所示。图中上平台坐标系为Om,Xm,Ym,Zm，“⊗”表示轴向垂直纸面向内；其他构件坐标系均用O,x,y,z表示，“⊙”为轴向垂直纸面向外。

1.上平台 2.上铰支座 3.上铰轴 4.活塞杆5.液压缸 6.下铰轴 7.下铰支座图1 Stewart平台实物结构

图2 Stewart平台基本构件的三维建模及坐标系

1.1 坐标系定义

Stewart平台的结构简图如图3所示。采用两类坐标系来描述各构件间的约束关系，即以大地为基准的固定坐标系Og,Xg,Yg,Zg和与构件固联的运动坐标系，各运动坐标系见图3。

图3中，上铰轴和下铰轴的坐标原点分别用Ai和Bi表示，i=1,2,…,6。AiBi表示Stewart平台的一条支腿。为与船舶运动对应，规定上平台绕Om，Xm轴为横摇运动，绕Om，Ym轴为纵摇运动。

1.2 基于变换层级的动态装配算法

采用姜洪洲等提出的基于变换层级的动态装配算法[8]，对Stewart平台进行空间的运动装配约束。对于并联运动机构的装配，要切断活塞杆和液压缸筒之间的滑动副，使其变为两套串联机构，再根据平台结构参数和各构件的基准坐标系，对其进行静态定位装配，见图4b；分别建立串联机构内各构件的层级关系，两套机构的父节点分别为上平台和与大地固联的下铰支座，见图4a。

图3 Stewart平台结构简图

图4 Stewart平台在Virtools中的装配及层级关系

平台在运动时，父节点的运动会影响子节点。当父节点的运动给定时，计算子节点的运动，是实现动态装配的关键。这需要在静态装配和运动学分析的基础上，通过构件的运动矢向来计算。具体包括4个子节点的角度计算，以单支腿Ai,Bi的运动学分析为例，坐标系和参数定义见图5，x(0)，y(0)，z(0)是构件坐标系O，x，y，z的初始坐标轴位置。

对于上半部分串联机构，上铰轴坐标系为：

(1)

其中，n5i,x、n5i,y和n5i,z为上铰轴坐标系轴向量；Avi为上铰轴相对上平台的轴向单位向量，见图5。上平台与上铰支座固联，上铰轴相对其父节点上铰支座、 活塞杆相对其父节点上铰轴分别有一个转动自由度θ5i和θ4i：

(2)

图5 单支腿Ai，Bi的运动学分析

(3)

对于下半部分串联机构，下铰轴坐标系为：

(4)

其中，n2i,x,n2i,y,n2i,z为下铰轴坐标系轴向量；Bvi为下铰轴在Og，Xg，Yg，Zg中的轴向单位向量，见图5。下铰支座与大地固联，下铰轴相对其父节点下铰支座、液压缸相对其父节点下铰轴分别有一个转动自由度θ3i和θ2i：

(5)

(6)

采用以上基于运动学分析的动态装配算法，给定上平台的运动规律，实时计算Stewart平台4个角度，实现其动态装配，如图4所示。某时刻液压缸活塞杆的伸缩量，可表示为：

Δd=di-l2(i=1,2,…,6)

(7)

其中，l2为工作零位时液压缸的初始长度；di为上下铰轴的距离：

(8)

2 船舶时域摇荡运动建模

图6 耐波性计算坐标系定义

船舶的频域方程用矩阵形式表达为[13]：

[-ω2(MRB+A(ω))-jωB(ω)+C]ξ=ζAFwave1

(9)

其中，ω为激励频率；MRB为船体惯性矩阵；A(ω)为附加质量矩阵；B(ω)为势阻尼矩阵；C为恢复力矩阵；ζA为波幅；Fwave1为单位波幅产生的一阶振荡波浪力列向量，j为虚数单位。采用基于势流理论的3D边界元法，计算矩阵A(ω)，B(ω)，Fwave1。由式(9)得到船舶运动的频域传递函数Hr(ω)为：

(10)

上式即船舶运动响应幅值算子RAOs(Response Amplitude Operators)。式中:

Q=[-ω2(MRB+A(ω))-jωB(ω)+C]-1

(11)

对于短峰不规则波有：

(12)

其中，S(ωk,θn)为第k个频率ωk、第n个波浪扩展方向θn的波谱，Δωk为激励频率间隔，Δθn为扩展浪向间隔。S(ωk,θn)用下式表达：

S(ω,θ)=S(ω)f(θ)

(13)

描述无涌浪无限风区无限水深、充分发展的海浪时，采用长峰波MPM谱[14]：

S(ω)=Aω-5exp(-Bω-4)

(14)

(15)

根据式(10)得到船舶时域的运动响应为：

(16)

其中，瞬时波面升高为：

(17)

其中，φkn为第k个波分量的相位角。

3 Stewart摇摆台三维运动模拟

3.1 摇摆台装配算法的试验验证

本节对Stewart摇摆台的动态装配算法进行试验验证。试验中的实物平台如图1所示，运动控制点选在上平台坐标系Om，Xm，Ym，Zm(0,0,-0.305 m)处，即上铰平面中心，单自由度横摇与纵摇的输入分别为幅值23 °、频率0.14 Hz的正弦信号，其发生与截止阶段有渐放与渐缩的过程，见图7。

图7 单自由度摇摆试验的输入信号

摇摆台分别做横摇和纵摇时，其活塞杆伸缩量的试验值与计算值对比见图8和图9。图中，计算值与试验值吻合很好，但计算中未考虑负载的影响，导致计算值略超前于试验值。

通过以上对比，验证了动态装配算法的正确性，可有效地进行Stewart平台运动学反解分析，还可用来做干涉、奇异校核。从而可采用本方法，对救助船进行三维空间的实时运动模拟。

图8 单自由度横摇的活塞杆伸缩量

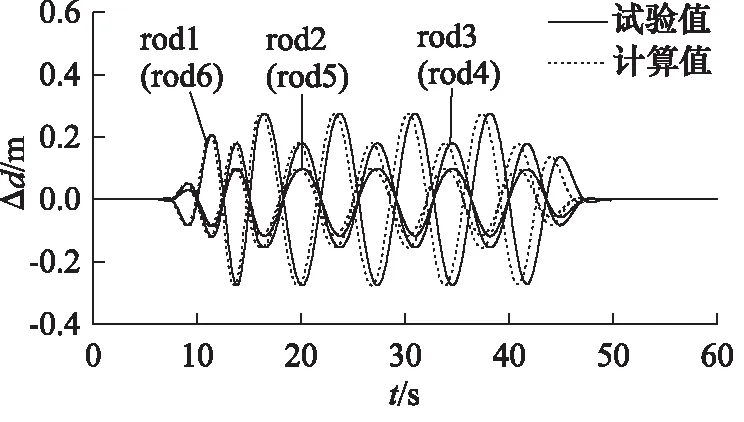
图9 单自由度纵摇的活塞杆伸缩量

3.2 救助船的运动模拟

以南海救111船为对象，在频域和时域计算其在深水不规则波中的运动响应，包括横摇和纵摇运动，作为Stewart平台运动的输入信号。计算条件设置如表1所示，波浪方向为90 °横浪。

采用式(10)来计算频域运动响应，计算点选在水线面上距舯后0.87 m的位置，横摇和纵摇运动RAOs的计算结果如图10和图11所示，分别给出幅值和相位随频率的变化。其中，横摇运动考虑了黏性阻尼修正。

表1 计算工况设置

图10 南海救111船横摇运动RAO

图11 南海救111船纵摇运动RAO

图12 南海救111船横摇和纵摇时域运动

根据式(16)来求解横摇和纵摇运动的时域响应，时厉变化如图12所示。计算结果中，横摇平均幅值在5°左右，最大值接近12°，纵摇平均幅值在2°左右，最大值接近4°，与设定的Hs=5.0 m对应6级海况吻合[10]。

将图12的横摇和纵摇时厉运动曲线作为信号同时输入到Stewart平台，运动控制点在上平台的中心Om，见图3。通过三维模拟计算，得到6个活塞杆伸缩量的时厉曲线，如图13所示。

图13 Stewart平台活塞杆伸缩量时厉曲线

在t=0时刻，活塞杆未伸出；当上平台运行到工作零位时，活塞杆随之运行到中位状态，此时伸缩量0；此后，各活塞杆围绕中位的伸缩量作周期性运动，大小随横摇角与纵摇角的变化而变化。

根据图13可知，将动态装配算法与三维运动模拟相结合，能够读取仿真或试验生成的历史数据，可有效地模拟救助船的摇荡运动。

4 结论

本研究针对救助船模拟器用的Stewart摇摆台，进行了南海救111船在短峰不规则波中的摇荡运动模拟。基于运动学分析和变换层级的动态虚拟装配算法，在Virtools的VSL编程环境中，实现Stewart平台在三维空间中的静态装配及实时运动约束装配，并通过试验验证了其正确性。采用耐波性理论，建立南海救111船在有义波高Hs=5.0 m的6级海况中的摇荡运动方程，给出横摇与纵摇的频域和时域运动结果。将横摇与纵摇的时厉运动曲线作为信号源输入到Stewart平台，实现对南海救111船在波浪中的摇荡运动模拟，给出平台各活塞杆在运动期间的伸缩量变化。

结果表明本研究的方法可有效地针对Stewart平台进行运动学反解分析和模拟救助船的摇荡运动，为配备有Stewart摇摆台的救助船模拟器的研究和相关标准的制定奠定基础。