负载口独立控制双联阀建模与特性分析
王 涛1,,刘 毅,黄方平,章卓耿,金列俊,高如君
(1. 安徽理工大学 机械工程学院,安徽 淮南 232001;2. 浙江大学 宁波理工学院,浙江 宁波 315100)
引言
在传统的液压系统回路中,常采用阀芯联动的液压方向阀对执行元件进回油进行控制,这就使得进出口的打开与关闭总是同时的,其进出口节流面积无法进行独立调节。而负载口独立控制技术,则利用双阀芯或多阀芯[1-2],解除了执行元件进出口之间的联动,能够实现液压执行元件进出口的独立控制,这增加了系统自由度,提高了系统对复杂工况的适应能力[3],在国防武器[4-5]和工程机械[6-7]智能化、节能化等领域具有广阔的应用前景[8]。其中负载口独立控制阀及其控制策略的优化设计是负载独立控制技术进一步提升的关键。
负载口独立控制技术最早由PALMBERG J.-O.教授系统地提出,他采用4个电液比例锥阀对电液负载恒压泵进行控制,增加了系统的柔性[9];张国泰等[10]提出一种带阀后压差补偿的负载口独立控制阀,降低了流量控制成本;赵翔宇等[11]提出一种新型螺旋先导独立负载多路阀,采用新型液压半桥先导放大结构设计,适用于大流量工作环境;ZHANG Q等[12]提出一种由5个双向滑阀组成的负载口独立控制系统,能通过软件编程实现不同的阀中位功能;DING R Q等[13]和徐兵等[14]提出一种负载口独立节能系统泵阀联合控制策略,降低了系统能耗;阮健等[15]通过大流量2D伺服阀控制器,实现了阀芯的精确控制,可用于负载口独立系统;ZHANG B等[16]则针对负载口独立系统设计了流量和压力耦合控制器,进一步提高了控制精度。
上述研究表明,负载口独立控制系统消除了进油口和出油口之间的耦合关系,可根据负载的变化运用不同的控制策略,使不同工作点都可以达到最佳的控制和节能效果,提高了控制系统的自由度,具有较高的控制精度。因此提出一种负载口独立控制双联阀[17],其结构简单,采用2个阀芯错位组合设计,能实现进出阀口节流面积精确、独立调节。
本研究主要介绍了负载口独立控制双联阀的工作原理,建立了其数学模型,并利用MATLAB/Simulink进一步分析了该阀在3种不同工况下的工作特性。
1 工作原理
图1所示为负载口独立控制双联阀控缸系统原理图,主要包括2个双联阀单元体、伺服电机、直线电机以及双出杆液压缸等,其负载口独立控制双联阀的立体结构如图2所示。其中,2个双联阀单元体阀芯的一端通过齿轮组与伺服电机相联,可由伺服电机带动同步旋转;而2个单元体阀芯的另一端分别与2个直线电机相联,可由2个直线电机独立带动2个单元体阀芯线性移动;如图1b、图1c所示阀口i、ii、iii、iv是由阀套沟槽与阀芯台肩沟槽所形成的通流阀口,阀口ii和阀口iv结构分布相同,阀口i和阀口iii结构分布相同,且不同时导通。如图1a中实线部分油路所示,液压油从油源P进入到第二双联阀单元体R2的f腔室,当伺服电机带动2个单元体阀芯从中位(阀口i、ii、iii、iv均不导通时阀芯所处的位置,相当于“O”形中位机能)旋转到如图所示的位置时,阀口iii打开,f腔室中的液压油通过阀口iii流入到e腔室,由于e腔室与双出杆液压缸的右腔室B相联通,从而推动液压缸活塞杆向左移动。同时,随着液压缸活塞杆向左移动,液压缸左腔室A中的液压油流入到第1双联阀单元体R1的b腔室,由于阀口i与阀口iii结构分布相同,阀口i也处于打开状态,因此b腔室中的液压油通过阀口i流入到a腔室,最终液压油回到油箱T以完成整个液压缸活塞杆向左移动的过程。同理,若伺服电机带动2个单元体阀芯再次从中位以反方向同步旋转相同的角度,阀口i(iii)关闭的同时阀口ii(iv)逐渐打开,如图1a虚线部分油路所示,液压油从油源P进入到第一双联阀单元体R1的c腔室,通过阀口ii流入到d腔室,然后流入到双出杆液压缸的左腔室A,推动液压缸活塞杆向右移动。同时,随着液压缸活塞杆向右移动,液压缸右腔室B中的液压油流入到第2双联阀单元体R2的g腔室,然后通过阀口iv流入到h腔室,最终流入到油箱T以完成整个液压缸活塞杆向右移动的过程。

1.伺服电机 2.齿轮组 3.阀芯 4.阀套 5.阀体 6.第一直线电机 7.第二直线电机 8.双出杆液压缸R1.第一双联阀单元体 R2.第二双联阀单元体 P.油源 T.油箱 A.液压缸左腔室 B.液压缸右腔室图1 负载口独立控制双联阀控缸系统原理图[17]
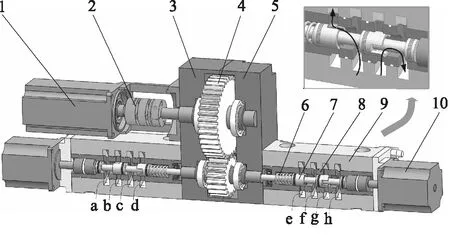
1.伺服电机 2.弹性联轴器 3.齿轮箱左盖板 4.齿轮组 5.齿轮箱右盖板 6.复位弹簧 7.阀芯 8.阀套 9.阀体 10.直线电机图2 负载口独立控制双联阀立体结构图
基于上述原理,通过对2个直线电机轴向进给量和伺服电机旋转角度的联合控制或单独控制,便可实现对进出阀口节流面积的精确、独立调节,这增加了系统控制自由度,有利于复杂功能的实现,可适用于复杂工况下的应用场景。
2 数学模型
分析时假定:供油压力ps恒定;回油压力p0约为0。图3所示为动力元件简化模型,当液压缸活塞杆向左移动时,阀口i、iii打开,阀口ii、iv关闭;当液压缸活塞杆向右移动时,阀口ii、iv打开,阀口i、iii关闭。

图3 动力元件简化模型
2.1 阀口通流面积控制方程
图4所示为工作过程中阀芯和阀套的配合关系,其中图4a、图4b分别展示了伺服电机在正转和反转情况下的阀口通流面积变化过程以及所对应的阀工作位置。分析时以该图视角观察,将阀芯逆时针旋转,即伺服电机顺时针旋转定义为正转;将阀芯顺时针旋转,即伺服电机逆时针旋转定义为反转。图中:阀口通流面积取决于控制边x1和x2之间的阀芯线性位移(xv)以及控制边θ1和θ2之间的阀芯旋转角位移(θ);控制边x1与阀套沟槽边界x3重合时为最大阀芯线性位移xvmax;阀芯旋转角位移θ对应弦长为yv,对应最大弦长为yvmax。

图4 工作过程中阀芯和阀套的配合关系图
图中黑色填充区域即为阀口通流面积Aj(j= i, ii, iii, iv),分析中将阀口i、ii、iii、iv均关闭时的位置定义为阀芯旋转角位移和线性位移的零位,即当Ai=Aii=Aiii=Aiv=0时,θ=xv=0,其中阀芯旋转角位移θ及其对应弦长yv满足以下关系式:
(1)
式中,n── 齿轮组传动比
n0—— 伺服电机转速
R── 阀芯台肩半径
由于伺服电机在正转和反转情况下的阀口通流面积增大和减小的过程完全一样,因此为了简化分析,均只考虑阀口通流面积从零逐渐增大的过程。于是,在这两种情况下的阀口通流面积变化分别可用以下方程来表示:
1) 伺服电机正转(左位: P-B; A-T)
xv1∈[0,x]
xv2∈[0,x]
(2)
2) 伺服电机反转(右位: P-A; B-T)
xv1∈[0,xmax]
xv2∈[0,xmax]
(3)
式中,xv1── R1单元体阀芯线性位移
xv2── R2单元体阀芯线性位移
Z── 阀芯台肩均布沟槽个数
2.2 阀口负载流量控制方程
根据节流孔流量计算公式,经过阀口i、ii、iii、iv的流量qj(j=i、ii、iii、iv)可以用以下方程来表示:
(4)
式中,Cd── 流量系数
ρ── 液压油的密度
pa── 液压缸左腔室的压力
p0── 回油压力,约为0
ps── 供油压力
pb── 液压缸右腔室的压力
与一般阀口匹配对称的阀不同,负载口独立控制阀由于其负载口独立特性,在动态时ps=pa+pb并不总是成立,这取决于进出阀口的开度大小。

则正向进油阀口压降为:
(5)
式中,k── 面积比Aiii/Ai
根据该阀结构原理,k=xv2/xv1,由此可知,仅当k=1,即xv1=xv2时,ps=pa+pb才成立。根据液压缸活塞受力平衡可得:
pb=pa+pL
(6)
式中,pL── 负载压力
将方程式(5)和式(6)联立可求得:
(7)
于是,该正向进油阀口压降可表示为:
(8)
当反向进油时,同理可推得:
(9)
于是反向进油阀口压降可表示为:
(10)
这表明,进油阀口压降大小由供油压力ps、负载压力pL和面积比k共同决定。
假定:由油液压缩性而产生的流量为0,若取动态时负载流量为流进流出液压缸的平均流量,则负载流量qL可表示为:
qL=[(qiii-qii)+(qi-qii)]/2
(11)
将方程式(4)、式(8)、式(10)代入式(11)中可得负载流量qL为:

(12)
考虑到伺服电机正转时,即0≤θ≤π/2Z时,Aii=Aiv=0;伺服电机反转时,即0≤θ≤-π/2Z时,Ai=Aiii=0。因此负载流量qL可以改写成如下形式:

(13)
利用线性化理论对阀进行动态分析时,流量增益是一个非常重要的性能参数,它往往对系统的稳定性、响应特性、稳态误差等有直接的影响,因此以下对阀芯角位移和线性位移单独控制工况下的流量增益进行分析。
首先为了便于线性化分析,假定:2Rsin(θ/2)≈Rθ,结合上述方程式(2)、式(3),阀口通流面积控制方程可改写成如下形式:
A(xv,θ)=Z·Rθ·xv
(14)
然后将上述方程式(14)代入式(13)中可以推导出该阀在正向进油时负载流量qL为:
(15)
于是,当k=1,即xv1=xv2,仅θ单独控制时阀芯角位移流量增益Kθ可简化为:
(16)
当xv1为一常数c,仅xv2单独控制时阀芯线性位移流量增益Kxv2可简化为:

(17)
其对应零位流量增益为:
(18)
(19)
由方程式(18)和式(19)可以看出,在上述假设条件下,该负载口独立控制双联阀的阀芯角位移零位流量增益和线性位移零位流量增益均取决于供油压力ps、阀芯台肩均布沟槽个数Z和阀芯台肩半径R;其中,阀芯线性位移零位流量增益还取决于进油阀口线性位移xv2、回油阀口线性位移c以及阀芯旋转角位移θ。
2.3 液压缸流量连续性控制方程
假定:忽略管道中的压力损失和管道动态以及液压缸的泄漏;液压缸每个工作腔内各处压力相等,油温和体积弹性模量为常数。
经过简化,可推导出流量连续性控制方程为:
(20)
式中,Ap── 液压缸活塞的有效面积
xp── 液压缸活塞位移
Vt── 液压缸2个腔室的总压缩容积
βe── 油液的有效体积弹性模量
2.4 液压缸与负载的力平衡控制方程
假定:液压缸活塞负载质量块沿光滑导轨移动,弹性力与阻尼力相比液压缸受到的力非常的小,可忽略不计,则液压缸与负载的力平衡控制方程可简化为:
(21)
式中,Fg── 液压缸输出力
m── 活塞及负载等效总质量
FL── 作用在活塞上的任意外负载力
3 特性分析
3.1 数值求解模型
根据上述数学模型,利用MATLAB/Simulink建立起该负载口独立控制双联阀控缸数值求解模型,如图5所示,具体包括4个子模块控制方程,分别为阀口通流面积控制方程、阀口负载流量控制方程、液压缸流量连续性控制方程和液压缸与负载力平衡控制方程。其中,数值求解中用到的主要参数如表1所示。

图5 负载口独立控制双联阀控缸数值求解模型

表1 数值求解主要参数
3.2 分析结果
1) 阀芯角位移和线性位移联合控制工况下供油压力与负载流量和活塞位移的关系
如图6曲面所示,在靠近阀芯旋转角位移和线性位移零位附近的地方可以实现非常微小节流阀口面积的控制,且该位置(A/Amax= 0.0~0.1)所围成的曲面面积相对较大,这表明在该位置范围内流量调节精度和灵活性相对较高,可应用于流量精密控制领域。同时,在阀芯角位移和线性位移行程末端附近可以达到较大的阀口通流面积,适用于大流量工况,虽相比零位附近其流量调节范围相对较小,但通过合适的控制策略设计,其流量控制精度依然可以得到较大程度的提升。

图6 阀口通流面积变化特性
具体的,如图7所示,若对伺服电机旋转角度和直线电机轴向进给量进行同步控制,使阀芯旋转角位移θ以20 Hz的换向频率从0匀速变化到π/4的同时,阀芯线性位移xv2也刚好从0匀速增加到6 mm,且在这过程中令xv1=6 mm保持不变,那么从图中可以发现:

图7 不同供油压力下负载流量及活塞位移变化特性
负载流量和相对应的活塞位移会随供油压力的增加而增加,且增速逐渐放缓;在不考虑任意外负载力以及其他因素干扰的情况下,阀芯角位移θ和线性位移xv2在0~30% 的工作行程范围内,随着供油压力从2 MPa 增加到10 MPa,负载流量可在0~30 L/min范围内进行调节,与此同时相对应的活塞位移可在0~5 mm 范围内进行调节;当阀芯角位移和线性位移达到最大工作行程时,10 MPa供油压力下可达到最大负载流量为186 L/min,且其最大活塞位移接近100 mm。
2) 阀芯角位移单独控制工况下供油压力与负载流量和活塞位移的关系
不考虑非线性因素的影响,根据式(16),动态时阀芯角位移流量增益与阀芯角位移无关,因此得出阀芯角位移单独控制时负载流量与阀芯旋转角位移之间存在正比例关系。
具体的,如图8所示,若对伺服电机旋转角度进行控制,使得阀芯旋转角位移以20 Hz的换向频率匀速增加到π/4,且在这过程中,始终令xv1=xv2=6 mm,那么从图中可以发现:在供油压力从2 MPa增加到10 MPa 的过程中,负载流量与阀芯旋转角位移始终成正比,这符合上述理论推导,因而该工况下具有良好的线性流量增益效果,其对应的活塞位移曲线趋于正弦曲线;当阀芯旋转角位移达到最大工作行程时,10 MPa 供油压力下负载流量能达到210 L/min,明显比上述联合控制工况下的负载流量大,这是因为该工况下阀芯线性位移xv2始终保持在最大工作行程,而联合控制工况下则与角位移同步增大,因而使其负载流量及活塞位移相对较大。

图8 不同供油压力下负载流量及活塞位移变化特性(θ单独控制;xv1=xv2=6 mm;f=20 Hz)
3) 阀芯线性位移单独控制工况下供油压力与负载流量和活塞位移的关系
不考虑非线性因素的影响,根据式(17),动态时若令阀芯角位移θ也为一常数,则阀芯线性位移流量增益还与线性位移xv2有关,因此不能得出阀芯线性位移单独控制工况下负载流量与阀芯线性位移成正比。于是结合式(15)、式(17)将qL(xv2)作二阶求导,发现xv2在0~6 mm区间内,qL(xv2)″<0,因此可以得出阀芯线性位移单独控制时负载流量与阀芯线性位移之间存在凸函数关系。
具体的,如图9所示,若对直线电机轴向进给量进行控制,使得阀芯线性位移xv2以20 Hz的换向频率匀速增加到6 mm,且在这过程中,始终令xv1=6 mm,θ=π/4,那么从图中可以发现:在供油压力从2 MPa增加到10 MPa的过程中,负载流量与阀芯线性位移之间并不是正比例关系,该曲线有向外凸的趋势,且供油压力越大,向外凸的趋势越明显,供油压力越小,向外凸的趋势越不明显,甚至逐渐趋于正比例关系,结合式(17)可得出是因为供油压力的大小影响了阀芯线性位移流量增益的大小;当阀芯线性位移xv2达到最大工作行程时,10 MPa供油压力下负载流量能达到225 L/min,活塞位移接近160 mm,相比上述2种工况,这种工况下的负载流量和活塞位移最大,这与阀口控制边宽度设计有关,相同情况下,单位时间内阀芯线性位移移动的距离大于角位移移动的距离,因此阀芯线性位移对阀口通流面积的影响程度相对较大,这就使得阀芯线性位移单独控制工况下的负载流量及活塞位移相对较大。

图9 不同供油压力下负载流量及活塞位移变化特性(xv2单独控制;xv1=6 mm;θ=π/4;f=20 Hz)
4 结论
(1) 阀芯角位移和线性位移联合控制工况下,在其工作行程零位附近,可以实现微小流量及活塞位移的稳定控制,且在该位置范围内流量调节精度和灵活性相对较高,可应用于流量精密控制领域;同时,在阀芯角位移和线性位移工作行程末端附近可以达到较大的负载流量及活塞位移,可适用于大流量、大行程工作场景,通过合适的控制策略设计,其流量控制精度可以得到进一步地提升;
(2) 阀芯角位移单独控制工况下,当阀芯旋转角位移达到最大工作行程时,相比联合控制工况,同样供油压力下负载流量及活塞位移较大;不考虑非线性因素的影响,其负载流量与阀芯旋转角位移成正比,因而该工况下具有良好的线性流量增益效果,其对应的活塞位移曲线趋于正弦曲线,可满足流量线性控制要求;
(3) 阀芯线性位移单独控制工况下,当阀芯线性位移达到最大工作行程时,相比上述2种工况,在同样的供油压力下能获得最大的负载流量和活塞位移,这使得该工况下系统具有较高的灵敏度,有利于实现大流量快速响应动作;不考虑非线性因素的影响,其负载流量与阀芯线性位移之间存在凸函数关系,且供油压力越大,向外凸的趋势越明显,供油压力越小,向外凸的趋势越不明显,甚至逐渐趋于正比例关系,因此在该工况下较小的供油压力有利于流量的线性控制。
以上研究表明该负载口独立控制双联阀能通过进出阀口节流面积的独立调节实现3种控制工况下流量和活塞位移的高精度控制,具有较高的灵活性,一方面可为阀芯旋转式负载口独立控制阀的设计分析提供借鉴,另一方面可为复杂工况下流量和压力的匹配补偿控制提供新思路。

