从一道联赛预赛题谈广义Prouhet球面的性质*

(惠州市实验中学，广东 惠州 516008)

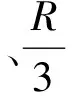
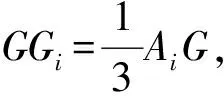
(2019年内蒙古自治区高中数学联赛预赛试题第9题)

笔者应用向量方法得到了赛题较为简洁的证法，并由此得到了四面体A1A2A3A4的广义Prouhet球面的几个有趣性质.现整理出来与读者分享，为叙述方便将上述试题记为性质1，即：

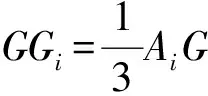
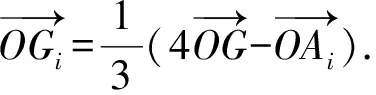
由于G是线段OH的中点，从而

代入上式可得

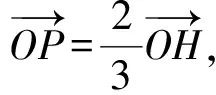
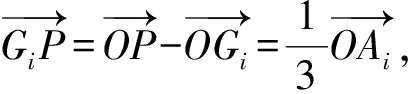
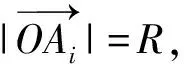
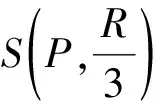
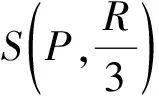
证明由题意可知

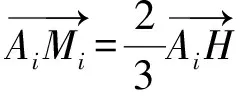
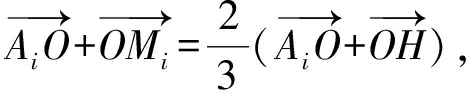
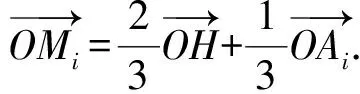
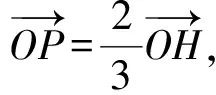
而顶点Ai(其中i=1,2,3,4)在球面S(O,R)上，故

因此

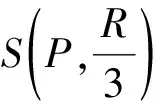
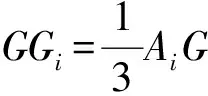
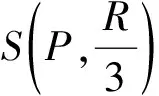
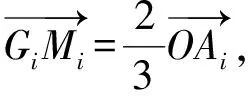
因此

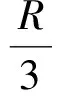
综合性质1～3，可得：

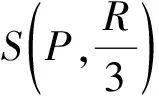
实际上，在性质4中，当四面体A1A2A3A4为垂心四面体时，令点H为其垂心，就得到了如下命题：

这就是1863年法国数学家Prouhet将三角形的九点圆定理类比推广到垂心四面体中得到的结论，由此产生了Prouhet球面的概念.