变革悄然而至，你觉察到了吗?*——2019年全国数学高考试题亮点记

(永登县第六中学,甘肃 永登 730300)

“断臂维纳斯”“嫦娥四号中继星‘鹊桥’”“参数云”“独孤信的印信”“概率与数列综合压轴”……作为师生的你，最近是否会被这些“热点”霸屏？2019年全国数学高考卷呈现出诸多亮点，有很多创新，可谓精彩纷呈.笔者对2019年全国数学高考卷的“亮点”进行了整理、分析，并对教师教学提出相应建议.

1 试题亮点

1.1 解答题次序变化较大

与2015—2018年全国数学高考卷相比，2019年全国数学高考卷的解答题次序有较大变化.全国卷Ⅰ理科试题将圆锥曲线、导数提前至第19，20题，第21题概率与数列综合压轴；文科试题将概率大题提前至第17题，第18～21题分别为数列、立体几何、导数、圆锥曲线.全国卷Ⅱ理科第17～21题的次序分别为立体几何、概率、数列、导数、圆锥；文科第17～19题的次序分别为立体几何、数列、统计.全国卷Ⅲ理科、文科第17，18题分别概率统计、解三角形，第20，21题分别为导数、圆锥曲线.

1.2 数学文化大放异彩，试题璀璨夺目

( )

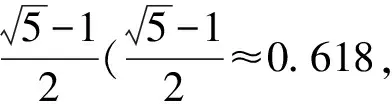
A．165 cm B．175 cm C．185 cm D．190 cm

(2019年全国数学高考卷Ⅰ理科、文科试题第4题)

分析本题渗透数学美，主要考查逻辑推理与数学运算素养．设人体脖子下端至腿根的长为xcm，肚脐至腿根的长为ycm，则

得x≈42.07 cm,y=5.15 cm．又其腿长为105 cm，头顶至脖子下端的长度为26 cm，可得其身高约为

42.07+5.15+105+26=178.22，

接近175 cm.故选B．

图1

例2我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，如图1就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是

( )

(2019年全国数学高考卷Ⅰ理科试题第6题)

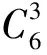
故选A．

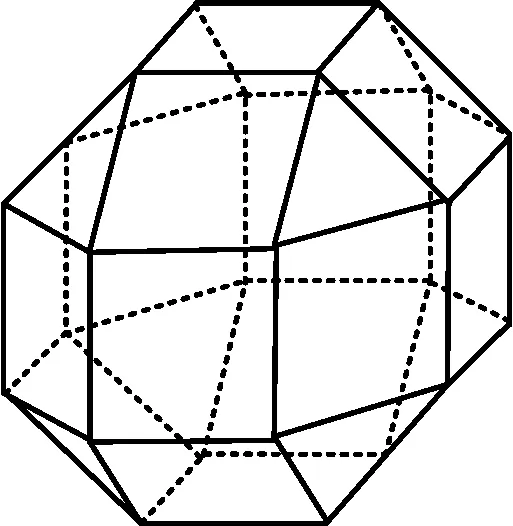
图2

例3中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图略).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1，则该半正多面体共有______个面，其棱长为______(本题第一空2分，第二空3分).

(2019年全国数学高考卷Ⅱ理科、文科试题第16题)

分析本题融入中国特有数学文化，主要考查直观想象素养.第一空可数出来，第二空需在正方体中简单还原出物体位置，利用对称性与平面几何知识解决．由图2知，该半正多面体共有26个面．如图3，设该半正多面体的棱长为x，则AB=BE=x，延长BC与FE交于点G，延长BC交正方体棱于点H.由半正多面体的对称性可知，△BGE为等腰直角三角形，从而

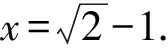
1.3 问题情境新颖多变，试题耳目一新

例42019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，我国航天事业取得又一重大成就.实现月球背面软着路需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地球月拉格朗日L2点的轨道运行，L2点是平衡点，位于地月连线的延长线上.设地球的质量为M1，月球质量为M2，地月距离为R，L2点到月球的距离为r，根据牛顿运动定律和万有引力定律，r满足方程

( )

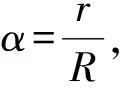
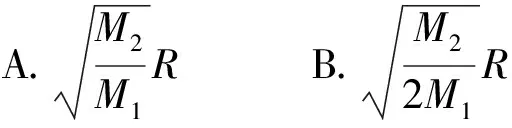
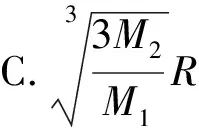
(2019年全国数学高考卷Ⅱ理科试题第4题)

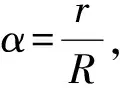
得

即

解得

从而

故选D.

全国卷Ⅰ文科第17题设置商场服务的现实情境考查统计知识；全国卷Ⅱ文科第3题设置“一带一路”时政情境考查理逻辑推理，理科第13题、文科第14题设置高铁现实情境考查统计知识；全国卷Ⅲ理科第3题、文科第4题设计我国古典四大名著情境考查统计知识，理科、文科第16题结合3D打印现实情境与物理科学情境，考查立体几何相关知识,文科第17题设置生物与化学科学综合情境考查统计知识.这些试题在众多的纯数学情境试题中“脱颖而出”，让人耳目一新.

1.4 打破常规命题模式，问题不落窠臼

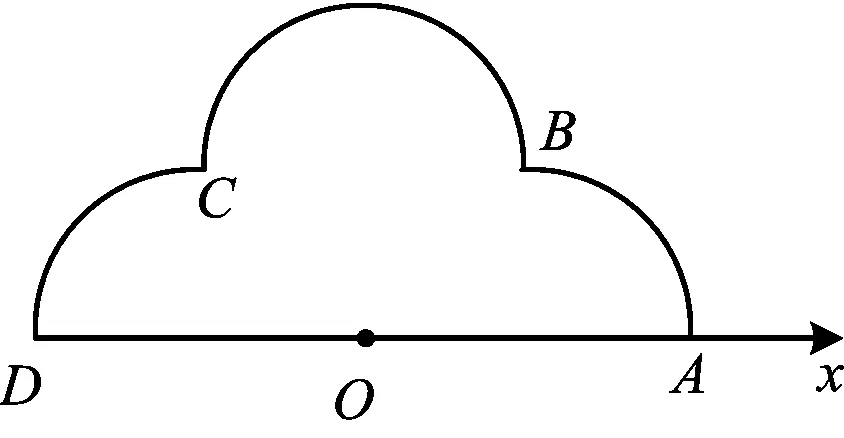
图5

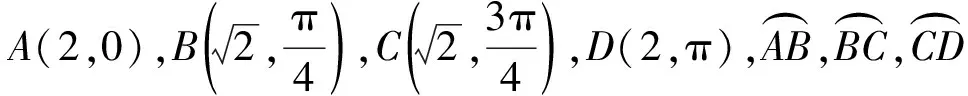
1)分别写出M1，M2，M3的极坐标方程；

2)略.

(2019年全国数学高考卷Ⅲ理科、文科试题第22题)

分析本题的创新之处在于打破常规命题模式，并非常见的极坐标与直角坐标互化，而是考查极坐标中过极点的圆的方程.因为题中要求的是弧，所以要注意方程中θ的取值范围.由题意，3个圆的直径都是2，并且都过原点，因此

1.5 知识考点融合交汇，试题深广度并存

例6为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物实验．实验方案如下：每一轮选取两只白鼠对药效进行对比实验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮实验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止实验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮实验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β，一轮实验中甲药的得分记为X．

1)求X的分布列.

2)若甲药、乙药在实验开始时都赋予4分，pi(其中i=0，1,2,…，8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1(其中i=1,2,…,7)，且a=P(X=-1)，b=P(X=0)，c=P(X=1)．假设α=0.5，β=0.8．

①证明：{pi+1-pi}(其中i=0,1,2,…,7)为等比数列；

②求p4，并根据p4的值解释这种实验方案的合理性．

(2019年全国数学高考卷Ⅰ理科试题第21题)

分析本题将离散型随机变量与数列巧妙结合，考查数学抽象、逻辑推理、数学运算等数学核心素养.题干较长，需耐心读题体会其中之意，利用递推关系式证明等比数列、累加法求解数列通项公式和数列中的项，问题就会迎刃而解.

1)由题意,X的可能取值为：-1，0，1，可求得

P(X=-1)=(1-α)β,

P(X=0)=αβ+(1-α)(1-β),

P(X=1)=α(1-β),

故X的分布列如表1所示：

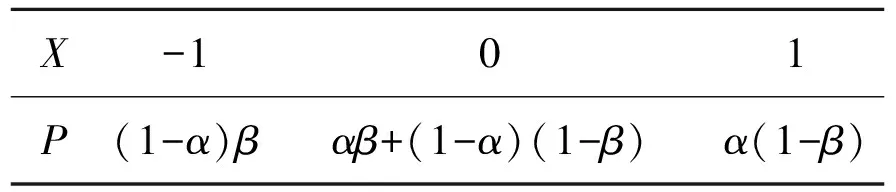
表1 X的分布列

2)①因为α=0.5，β=0.8，所以

a=P(X=-1)=0.4，

b=P(X=0)=0.5，

c=P(X=1)=0.1,

可得

pi=0.4pi-1+0.5pi+0.1pi+1，

即

0.5pi=0.4pi-1+0.1pi+1，

从而

0.4(pi-pi-1)=0.1(pi+1-pi)，

得

于是{pi+1-pi}(其中i=0,1,2,…,7)为等比数列．

②{pi+1-pi}(其中i=0,1,2,…,7)的首项为p1-p0=p1，可得

p8-p7=p1×47，

p7-p6=p1×46，

…

p2-p1=p1×4.

以上7个式子相加，得到

p8-p1=p1×(47+46+…+4),

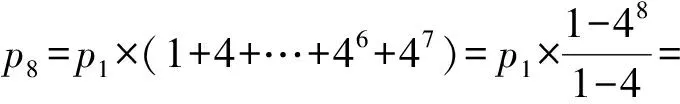
得

再把后面3个式子相加，得

p4-p1=p1×(4+42+43)，

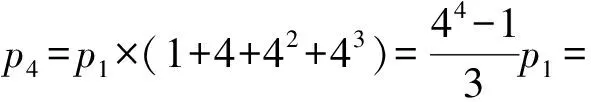
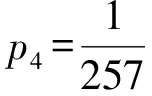
2 数学教学建议

《普通高中数学课程标准(2017年版)》(以下简称《新课标》)指出：数学高考命题，应围绕数学内容主线，聚焦学生对重要数学概念、定理、方法、思想的理解和应用，强调基础性、综合性；注重数学本质、通性通法；融入数学文化；应有一定数量的应用问题，考查学生的思维过程、实践能力和创新意识，问题情境设计自然、合理[1].2019年是《新课标》颁布的第二年，高考数学变革、创新顺理成章.“变则通，通则达”，为更好地应对变革，对教师教学提出以下建议：

2.1 践行数学文化，提升文化素养

以传统文化为载体，加强数学传统思想文化的渗透，将国家的育人要求与高考选拔相结合，是近几年高考新动向.高考具有导向性，随着高考卷中数学文化试题的大量出现，数学文化已被广大师生接受并认同.从认同到内化需要身体力行，需要教师有意识地结合相应教学内容，在日常教学中渗透数学文化，引导学生了解数学的发展历程，认识数学在科学技术、社会发展中的作用，感悟数学的价值，以提升学生的科学精神、应用意识和文化素养.

2.2 注重数学阅读，助力数学理解

苏联教育家苏霍姆林斯基曾说：“学会学习首先要学会阅读，一个阅读能力不好的学生就是一个潜在的差生.”从前面的考题不难发现，很多“亮点题”题目“长”且情境丰富，这就对考生的数学阅读能力提出了高要求.数学阅读不仅具有一般阅读的特点，还因数学语言的符号化、逻辑化以及抽象性、严谨性等原因，具有其特殊性.研究表明，中小学生数学阅读状况呈下降趋势，中学生对数学阅读的兴趣、态度、习惯等均不容乐观[2-3].因此，在日常教学中，教师要有意识地教授数学阅读策略、技巧，培养学生数学阅读兴趣和习惯，消除数学阅读障碍，助力数学理解.

2.3 抓主干搂枝叶，构建知识体系

高中数学知识点虽多，但都围绕函数、几何与代数、概率与统计、数学建模与数学探究等主干展开.高考试卷要在特定数量的试题中考查大多数知识点，势必大部分属于知识交汇融合的综合性题目.因此，教师在教学中要以数学学科核心素养为导向，引导学生抓主干，同时不忘搂枝叶，将数学知识点连成线、形成面、构成体，从整体上把握课程，提高灵活运用知识的能力，实现数学学科核心素养的形成和发展.