由一道中考题中“a的范围”求解说起*

(正余初级中学,江苏 海门 226153)

在初中数学中，函数是数与式的重要组成部分，其中二次函数更是重中之重.它是学生从常量数学向变量数学迈进的垫脚石，是衔接初高中内容的重要纽带，是学生应该掌握的基本知识.而伴随二次函数考查的一个重要考点，即“求‘a’的取值范围”，近年来成为各地中考数学命题者的不二选择.此类问题往往集函数、方程和不等式、数形结合、分类等于一体，综合性强，灵活度高,思维难度大,学生短时间内破题实属不易，为此笔者以2019年江苏省南通市数学中考试题第26题为例，精选考题加以分类、剖析，发掘问题的内涵、外延，以期破解相关“a的取值范围”求解问题，如有不当之处，敬请批评指正．

类别1“a”是二次项系数，抛物线图像与坐标轴的交点在一定的取值范围之内.

例1关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根都在-1和0之间(不包括-1和0)，则a的取值范围是______．

(2015年江苏省南通市数学中考试题第18题)

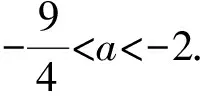
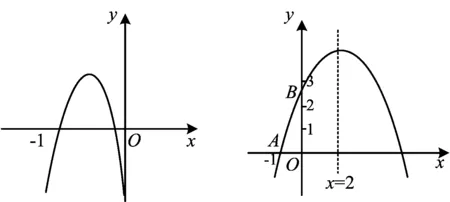
图1 图2

例2如图2，二次函数y=ax2+bx+c的图像与x轴交于点A(-1，0)，与y轴的交点B在(0，2)与(0，3)之间(不含点A,B)，直线x=2为对称轴，则a的取值范围是______．

(2018年四川省达州市数学中考试题第10题改编)

方法总结本题是明确的二次函数问题，但难点是想不到把多参数化为单参数.一旦能抓住确定条件A(-1，0)和对称轴为直线x=2，接下来的问题就较为简单了.具体思路为：由x=2，可得b=-4a；由A(-1，0)，可得a-b+c=0，进而得c=-5a,于是二次函数就化简为

y=ax2-4ax-5a.

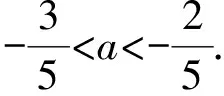
类别2“a”是二次项系数，抛物线图像与某线段的交点只有一个.

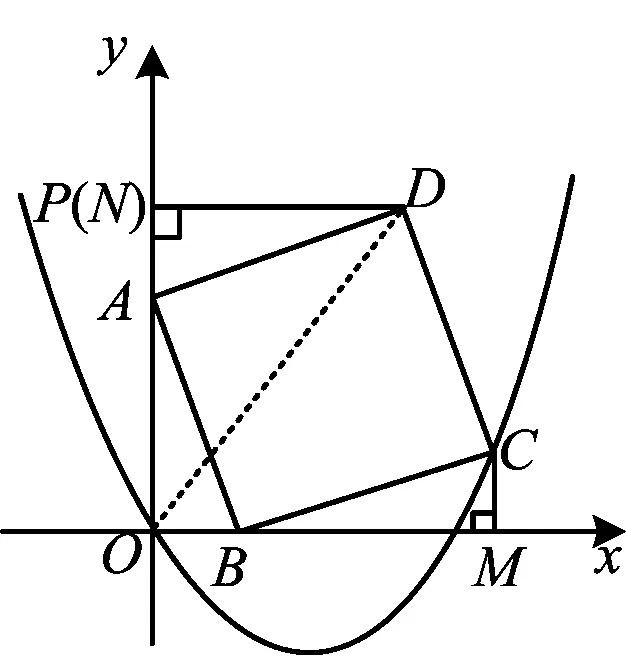
图3

例3如图3，在平面直角坐标系中，已知点P(0，4)，点A在线段OP上，点B在x轴正半轴上，且AP=OB=1，以AB为边在第一象限内作正方形ABCD,过点C，D依次向x轴、y轴作垂线，垂足为M，N.设过点O，C的抛物线为y=ax2+bx+c．联结OD，若此时抛物线与线段OD只有唯一的公共点O，求a的取值范围．

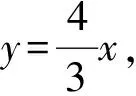
题目条件是“与线段OD只有唯一的公共点O”，但在解题时可以放大线段的条件，用直线的交点来考虑问题，得到

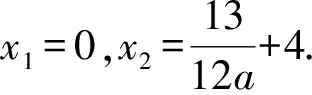
例4在平面直角坐标系xOy中，直线y=4x+4与x轴、y轴分别交于点A，B，抛物线y=ax2+bx-3a经过点A，将点B向右平移5个单位长度，得到点C.若抛物线与线段BC恰有一个公共点，结合函数图像，求a的取值范围.

(2018年北京市数学中考试题第26题改编)

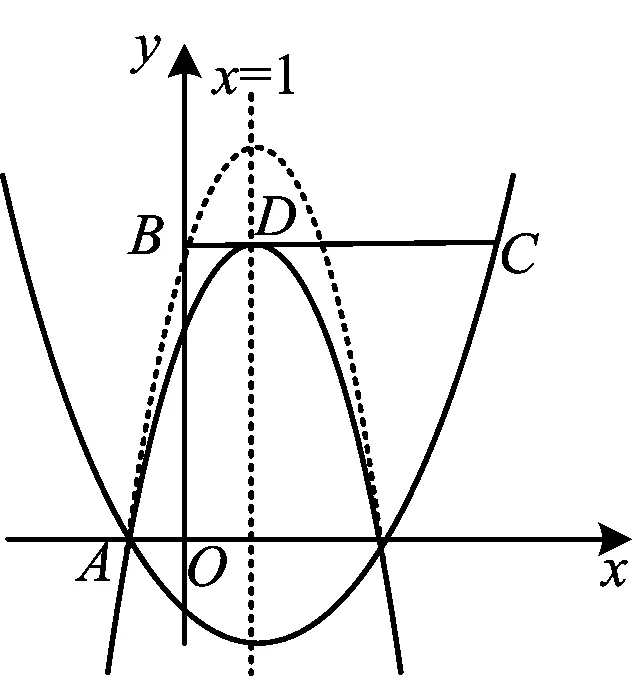
图4

方法总结本题的抛物线是两参数过定点的形式并且需要分类讨论，思维含量大，学生非常容易出现束手无策或漏解.这种类型的问题我们通常可以通过代入定点进行消参，然后借助图像(如图4)找到极端位置，再用变化的眼光研究找到破题入口.此题稍作处理即得新的抛物线y=ax2-2ax-3a，接下来的处理办法与例3类似.

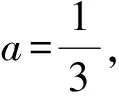
类别3“a”是二次项系数，函数值大于(或小于)某常数恒成立.

例5已知二次函数y=ax2+(2a+1)x+1(其中a≠0)．若对于任意的-1≤x≤1，y≥0恒成立，求实数a的取值范围．

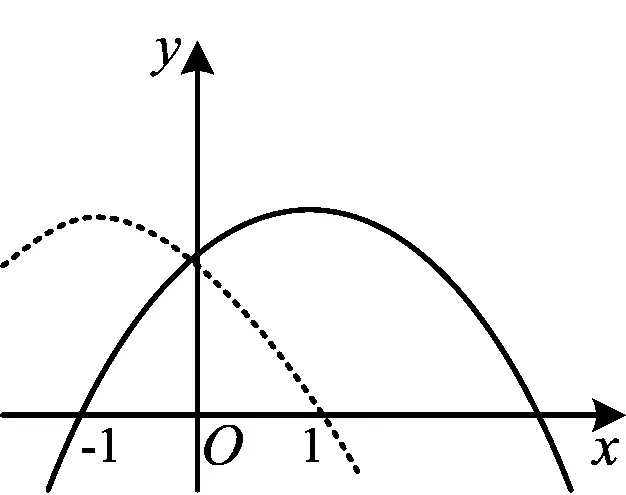
图5

方法总结本题属于二次函数值恒成立问题.如果自变量x的取值范围是任意实数，恒成立对学生就不构成困难了，但本题的x是对于任意的-1≤x≤1，这种情况学生不太会处理.常规方法还是数形结合，考虑利用二次函数图像(如图5)的直观性来辅助处理．因为a在二次项系数和一次项系数上，影响抛物线的开口方向、判别式、对称轴等，带来不少麻烦，这时不妨从常数项为1入手，即抛物线过y轴上定点(0，1)，这样问题就变得容易多了.

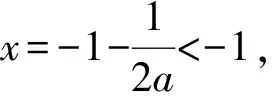
类别4“a”是二次项系数，抛物线顶点在某个封闭区域内运动.

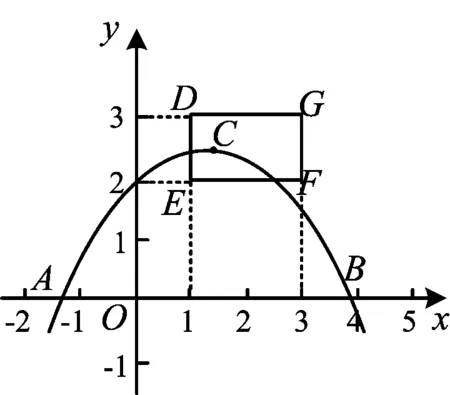
图6

例6如图6，抛物线y=ax2+bx+c与x轴的一个交点A在点(-2，0)和(-1，0)之间(包括这两点)，顶点C是矩形DEFG上(包括边界和内部)的一个动点，则a的取值范围是______．

方法总结本题是动抛物线问题，开口方向已经定好.本题中“a的取值范围”求解，即要找到抛物线开口大小的两个极端位置.题目中的条件发掘要充分利用图像，学会读图，使图像开口最大，则需要点A经过最外点(-2，0)，点C落在点F上与点A的水平距离最大，抛物线在x轴上截得的线段最长，顶点离x轴最近，这样抛物线的开口最大，因为开口向下，所以a的值也最大.类似地，点A经过最内点(-1，0)，点C落在点D上与点A的水平距离最小，抛物线在x轴上截得的线段最短，顶点离x轴最远，这样抛物线的开口最小，因为开口向下，所以a的值也最小.当这两个极端位置被找到，问题就很好解决了.

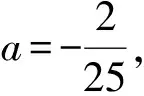
结合以上实例的解答过程，对此类问题的解法总结为：充分利用题目中所给的具体点的坐标和图像运动过程中的极限位置，巧妙使用数形结合，则解题思路就会“拨开云雾”，豁然开朗．

类别5“a”是常数项，抛物线图像在某范围内与定直线有两个交点.

例7设函数y=x2-4x+3a+2(其中a为常数).

1)请写出二次函数的3条性质；

2)在同一直角坐标系中，若该二次函数的图像在x≤4的部分与一次函数y=2x-1的图像有两个交点，求a的取值范围.

(2019年江苏省南通市数学中考试题第26题)

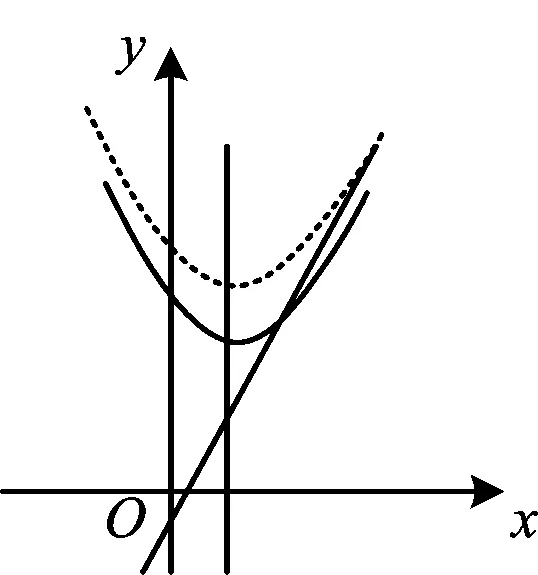
图7

方法总结本题是江苏省南通市数学中考试题第26题，其第2)小题属于压轴题，对学生而言是有一定难度的.“二次函数的图像在x≤4的部分与一次函数y=2x-1的图像(如图7)有两个交点”的问题，从知识点考查来看，是属于函数与方程及不等式的问题，是二次函数与方程的解都小于等于4的问题，但若真从这个角度去破题，则其运算及计算难度不是一般的大.其实本题抛物线的开口方向、开口大小以及对称轴都是定的，不定的是常数项，它将影响抛物线图像的上下位置，同时一次函数的直线图像又是定的.

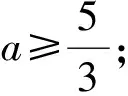
消去y得

x2-6x+3a+3=0，

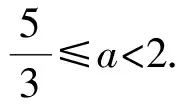
由此可知对学生数形结合思想的培养之重要性，教师要不断引导学生在数学学习过程中逐步感悟和强化它.数学结合对于数学问题的解决具有强大的功效，而本题对于这一数学思想考查之妙，就是考试者心中有“形”而题中则无图，最终解题又得依赖图形直观辅助思考.

每年此类型的中考试题都会给人以耳目一新之感，深感命题者的功底和用心.但站在学生角度再看此类问题，实质都是一种对自身思维能力的挑战.笔者多年来一直对此类问题给予关注，通过收集试题类比、归纳和整理，概括出以上5个类别并形成3点破题心得.

1)函数、方程、不等式有关系，要在心中常联系.

函数是初中阶段“数与代数”的重要内容，也是初中学生比较难以理解与掌握的数学概念之一.课标中对其教学是呈螺旋式上升的，在第三阶段的教学重点就是引导学生理解函数与方程之间、与不等式(组)之间的内在联系，帮助学生打通知识之间的壁垒，真正形成融会贯通之态[1].当a是二次项系数时，a的正负决定抛物线开口方向，当a>0时，开口向上；当a<0时，开口向下；a的绝对值决定抛物线开口大小，|a|越大，抛物线开口越小．这时抛物线图像的不确定，主要是由开口方向与大小的不确定所致，在分类讨论之后利用极端位置形成破题思路，化为方程或不等式(组)即可实现变“不确定”为“确定”，从而分散问题的难点使问题获得解决．

2)数形结合要奏效，画出草图不可少.

中考试卷中很多类似的二次函数题都是有“形”无图题(如例1，4,5,7都如此)，在做题时要求能洞察问题的本质，将内隐的图形显性化.抛物线图像有其典型的简洁美和对称美，图像的直观呈现在一定程度上可以诱发解题思路，再结合条件把数、式和图像结合起来进行思考，相互解释、相互补充，配上有理有据地思考和推理，就能形成破题思路.而这种以形助数、以数解形的思想，对整个中学数学乃至以后的学习，愈发的重要[2].平时教学中，教师应帮助学生积累一些常见的关于“a的取值范围”的类别，尤其是与特殊条件关系密切的解法模型，致使学生手中有“数”，眼中有“形”，心中有“法”.

3)以静制动能破题，极限位置要找准.

通过对此类中考试题的深入研究，问题的难点是抛物线图像的位置不确定，而不确定的原因又是“a”的取值是一个范围，而“a”的取值范围的求解又得求助于抛物线图像的位置，看似循环论证下的无解之境，实质在图形辅助之下，寻找已知的、固定的条件元素，挖掘条件的本质(如例1看似方程解的问题，实质是函数图像与x轴在一定范围内的交点问题；例7看似曲线与直线在一定范围内的交点问题，实质是方程与不等式问题等等)，这时就需要借助数形之间的关联，用数学的眼光进行审视，找到极端位置即是问题的破解之道.在平时的教学中应该让学生体验不同思考方式的问题情境，其中用“极限法”思想来作为破解动态几何问题的解题策略，也是符合“从特殊到一般”认知规律的，极限位置也是众多动态位置中的一种，对极限情况下的研究思路和所得结果，对一般位置的研究同样有着积极的辅助作用[3]．

本文例题数量不多，诚如数学教育家波利亚曾说过:“一个专心、认真备课的老师能够用一个有意义但不复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域．”此类问题若能教会学生借助所画的图像，挖掘题目中的隐含关系，用发展变化的眼光去观察、研究图形，抓住极端位置以静制动，捕捉到此类问题的固定模型，寻找到“数”与“形”的奇妙联系，从而能有效解决“a”的取值范围问题．