课堂教学若干操作的有效性分析及改进*

(河埒教育集团水秀中学,江苏 无锡 214071)

有效教学是指遵循教育教学活动的客观规律，选用合适的手段和方法，尽可能地以较少的投入取得较好的教学效果．围绕减轻学生的学业负担，如何提升教学的效率呢？在影响效率的诸要素中，教学设计举足轻重，它是课堂教学的起点，反映着教师的教育理念和教学策略．设计是否合理、有效，从某种意义上看决定了课堂教学的成败．本文通过案例，对课堂的导入方式、例题与练习等主要环节存在的一些低效、甚至无效的设计作一点剖析与改进，以寻求提升课堂有效性的途径．

1 异化的“合作学习”——因费时、费力而低效、无效

小组“合作学习”作为一种教学模式走进课堂，为新课改所倡导.这种模式可使学生人人参与学习过程，人人得到锻炼机会，有利于培养合作精神.然而在具体的实施过程中，存在不少异化现象.

1.1 镜头回放

镜头1初二“一次函数的图像”教学中，教师在巩固环节呈现例题：对于函数y=(m-1)x+2m+1的图像.1)若y随x的增大而增大，求m的范围；2)若图像经过第一、二、四象限，求m的范围.操作时，教师要求用“小组合作讨论”解决该问题，前后座位4人一组，共用时5～6分．

镜头2在“体验游戏公平与不公平”的课堂上，教师布置了“抛筹码”的游戏，要求小组合作讨论游戏的公平性.教室里一下子热闹起来，发口令的、抛筹码的……，教师见状也面露喜色，可是听课教师也发现：有的小组学生在做重复的事情，抢着抛筹码，觉得比较好玩，没有学生做记录；有的小组部分学生不动手，在看“热闹”……

1.2 效能分析

显然，镜头1中的题目是一道较为简单的问题．第1)小题由m-1>0，可得m>1；第2)小题只需借助图像，得m-1<0且2m+1>0，再解一次不等式组即可.对于这样一道中等层次的学生都能求解的题目，有必要进行小组讨论吗?笔者认为，只有那些结论不确定的探究题型或多结论的开放题型以及有一定难度的综合题型等，才需要通过小组“合作学习”来解决，同时也要考虑讨论的有效性．可以独立思考及完成的，就不必费时地小组合作.表象的多此一举，实质是对“合作学习”的浅层次理解，结果造成了效率的低下！

对于镜头2，这类游戏性质的动手合作，学生们十分兴奋，但小组成员分工不明，责任分散.有的仅是热闹的表面参与，缺乏有效的思维跟进，个别学生还游离课堂之外.

类似的“合作学习”在公开课中并不少见，有的是“作秀”的“合作”，有的是“分工不明”的“合作”，有的留时太少、“匆匆”的“合作”，这些异化的“合作学习”，既浪费时间，也浪费精力，且效果低下甚至无效．

1.3 提升有效性

为提升“合作学习”的效果，先要考虑是否有必要“合作”，因课堂的限时性，应坚决避免“作秀”．对于有必要进行的“合作学习”，应做到以下几点：

1)实施前要让学生明确目标，合理分组，适当减少小组规模，以防止学生滋生“混水摸鱼”的侥幸心理，使学生体会到是小组合作，而不是依靠他人；

2)实施中要做到分工细致，落实到每个小组成员，强化学生的角色意识、合作意识，增强责任感；

3)实施后要有检查、反馈，如果合作后的成果较多，还可布置该议题的相关作业．

2 含糊的“过程诊断”——因矫正问题的力度不够而低效

2.1 镜头回放

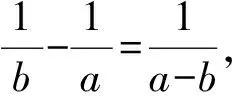
课堂操作：第一步，教师请甲、乙两位中等层次的学生上黑板板演．

(a-b)2=ab,

(1)

目标式化简，得

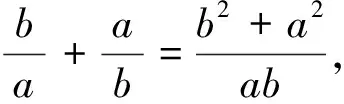
(2)

乙：同生甲得式(1)，展开移项，得

a2+b2=3ab,

(3)

目标式化为

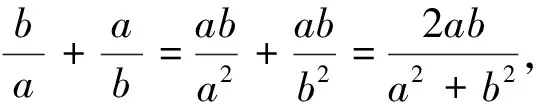
(4)

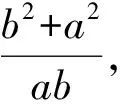
2.2 效能分析

该教师教学生如何解答，虽然也指出生乙的通分错误，但没能指出生甲思路受阻的原因，这恰恰是问题的关键．另外，还有其他解答方法吗？出现错误该如何矫正呢？这些问题都没能讲清楚．

2.3 提升有效性

面对学生出现的问题，如何分析、有效利用资源，提升教学效果呢？

1)除了要让学生板演或投影解答过程，还需要指出思路受阻的原因，让学生理解问题的来龙去脉，便于产生自觉矫正的行动.

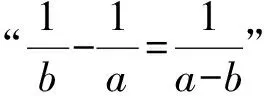
4)反思、归纳这一类问题的基本处理方法：从条件、目标两头“凑”，强化解题的目标意识．

3 过度的“细化处理”——因没有必要且费时过多而低效、无效

3.1 镜头回放

在初三“分式方程及应用”的一堂复习课上，某校初三年级两个普通班有两种不同的操作：

镜头4在复习解分式方程时，呈现问题后，让学生回答，教师对每一步都问为什么，师问、生答，然后归纳一般步骤、板书，教师讲得很细，强调得也很到位.这道解分式方程问题花费5～6分．在复习分式方程时出示了3道应用问题：两道例题、一道同步练习.第一道是行程问题，第二、三道是工程问题，教师在讲解时都用了表格，分析前后两次的速度、时间、路程与效率、时间、总量的关系.3道问题中有两道是教师列表、学生填空的．课堂上教师在指导列表时，有几位学生早早地把方程都列好了，望着教师，显得悠闲自得的样子．

镜头5在复习解分式方程时，用了与镜头4一样的问题，教师问该怎么解分式方程？全班学生几乎异口同声：去分母，解整式方程，然后检验．教师只是对学生出现的去括号、符号、忘记检验等问题，做点矫正、强调．在这一环节，时间少用了3分．对分式方程的应用问题，以一道工程问题为例子，与学生一起审题、理清其中的数量关系，寻找等量关系，另两道让学生练习，可以列表，也可以不列表，但重在分析等量关系，分析学生的易错点．时间少用了近5分．

3.2 效能分析

复习课上解一道分式方程用了5～6分，每一步都问为什么，每一步都细致讲，有这个必要吗？效果真的就好吗？从两个平行班的课堂反馈来看，学生主要错在两处：一是单位忘了换算；二是“被减数”与“减数”弄反了．教师只需把这两点讲清即可．问题出在教师的心理，对学生“不放心”，以为学生这也不行、那也不会，只有通过自己强调后才放心．其实不然，学生会的东西，可能听不进去，甚至有点抵触情绪．

以上问题具有一定的普遍性，如在一堂“二次函数”的复习课上，教师见有人听课，对于每一步都处理得很细，但只完成计划的70%，且一堂复习课，“尖子生”收获不大，显然是低效的．久而久之，还会降低一些“尖子生”的兴趣和信任度，不利于教学质量的提升！

3.3 提升有效性

教学的有效性离不开针对性，根据学生、教材的特点，详略得当地实施．要通过常反馈获取信息，对于有的简单问题只需口答即可，对于一般的问题，通过举手反馈：若正确率达到90%，一般不讲；若正确率不超过70%，则要让学生暴露问题、一同矫正，视情况详讲，把握其“度”．提高课堂45分的利用率，训练到位，教学效果突出．

4 过多的“事前提示”——因缺乏判断机会、易错而无效[1]

4.1 镜头回放

镜头6在一堂初三“二次函数的复习课”上，教师出示问题：已知抛物线y=(x+1)2，若一条直线过点(1，0)，且与抛物线只有一个公共点，试求该直线的方程.

操作：教师提示学生先画示意图，然后提示在审题时要抓关键词：只有一个公共点；当学生在解答时，又问学生：可能有几种情况？……

4.2 效能分析

镜头中问题出示后，学生尚未思考，教师就急忙提示学生要这样、那样．类似的场景，不时出现在我们的数学课堂中，教师把学生“含在口里”，不断指引：往前、往后……，不断提示，这里有“坑”、那里有“洼”．其一，学生未来得及思考，教师就过早地提示，这岂不是在限制学生的思维？其二，在测试卷中经常有一些学生，审题不细，做了前问，漏了后问，不会自我矫正，缺乏判断机会，是否有教师的责任呢？有的课堂，教师给学生审题的时间、解题后反思的机会很少.如此“事前提示”，是低效甚至无效的．

4.3 提升有效性

有效的数学活动要在“做中学”，即先通过学生的尝试，或动手实验、或观察判断、或推理演算，获得一些感性认识，再与同伴合作交流，必要时辅之以教师的点拨引导，以解决问题．对于镜头中的问题，可让学生独立审题、找关键点、尝试画图．这样，有的学生想到一个解，有的学生想到两个解，教师再进行事后提醒、矫正．如果经常先让学生尝试，再“事后提醒”，促其反思，就可以不断积累经验，使学生的头脑变得灵活，思维变得严谨．“一分为二”地看问题，我们也不是一味排斥“事前提示”，譬如有的公式容易混淆、记错，不妨“事前提示”，以树榜样；有的问题过于复杂或头绪太多，学生经思考后，仍难寻突破口，教师可做必要的“事前提示”，以提高课堂效率．

当然，课堂操作还有不少低效现象，如有的数学课堂学生机械操练多、模仿多，而思考少，致使不少知识、方法不能内化为学生的；有的在临近中考前还依赖于“几何画板”的动态演示，而一旦离开电脑的支撑，考生将如何应对？看似有益于学生的理解，但从考试结果和思维层面分析，则为低效.这些问题都期待我们去思索与改进．

有效的教学操作，离不开有效的教学预设；变化的课堂、灵动的学生呼唤机智应变的教师，让科学合理的教学操作为课堂增效，以实现大家都期待且放心的减负．