借由多种表征,建立小数与十进分数的联系
符玲利 章勤琼
【摘 要】小数的认识是小学生对数系统认知的一个扩充,学习小数时,需要让学生建立十进制可以向小数部分延伸的认识。在《小数的初步认识》的教学中,可以淡化[310]米=0.3米这样的形式表達,抓住“把1十等分产生小数”这个过程,这也是“建立小数与十进分数的联系”的根本所在,并通过实物、图形、数轴等多种不同的表征方式,让学生建立起“十等分才能产生小数”以及“十份里的几份就是零点几”这两点的理解。
【关键词】小数;初步认识;分数;十等分;表征
【课前思考】
三年级学生已经初步认识了分数,知道将一个物体平均分成几份,表示其中的一份或几份可以用分数来表示;他们也具备1元=10角、1米=10分米的生活经验,了解一些简单价格表示的意义,如0.1元是1角。但为什么1角用0.1元来表示呢?1元等分成10份,1份是1角,学生顺向思考好像没有问题,但逆向思考1角是十分之一元却出现障碍,认知出现断层。如何将小数的意义和生活经验建构起来,需要通过十等分来做支撑。故本课选择学生熟悉的人民币、长度单位等素材,试图在学生已有认知基础上建立起十等分的概念,再借助操作提炼出一位小数的意义。
【教学内容】人教版三年级下册第七单元
【教学目标】
1.结合具体情境初步认识小数,会读、写小数,知道一位小数表示的意义。
2.经历观察、操作、辨析等过程,沟通分母为10的分数与一位小数之间的联系,培养学生的数感,渗透一一对应思想。
3.在交流的过程中充分发表自己的想法,培养勇于质疑的精神 ,形成严谨求学的科学态度。
【教学过程】
一、导入新课,初悟小数
1.谈话导入
师:同学们,一年级小朋友上课时遇到一个问题,他们的书上出现了一些不认识的数(如下图),你认识吗?
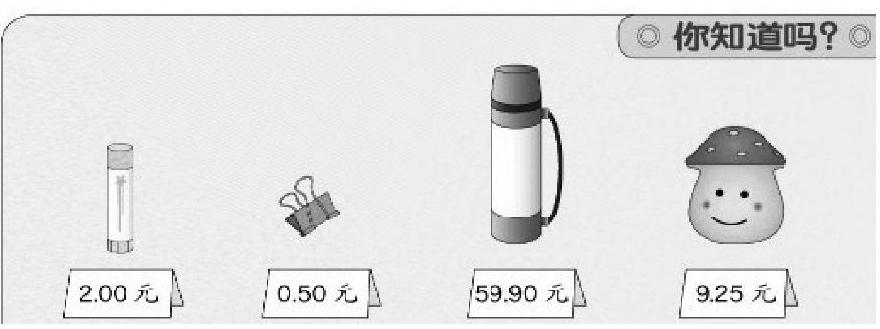
生:都有小数点。
生:不是,是小数。
师:是的,这些数叫小数,小圆点叫小数点,小数点左边是整数部分,小数点右边是小数部分。(板书课题:小数)
2.读小数
生:第一个是2元。
师:哦,固体胶的价格是2元,就读作2元吗?
生:二点零零元。
师:一起来读后面几个价格。
生齐读:零点五零元(零点五十元)。
师:我听到两种声音,小数部分的读法和整数部分一样吗?(学生无法肯定)其实小数部分的读法和整数部分不一样,小数部分要一个一个读,再来读一次。
生齐读:零点五零元、五十九点九零元,九点二五元。
3.生活中小数的意义
师:0.50元中的5表示什么意思? 9.25元中的5又表示什么意思?
生:0.50元中的5表示5角;9.25元中的5表示5分。
师:59.90元中的两个9分别表示什么意思?
生:59.90元中整数部分的9表示9元,小数部分的9表示 9角。
(思考:小数在生活中比较常见,学生并不陌生,结合具体情境学生能表述出各个数位上小数代表的实际意义,挖掘学生的生活经验,为后续深入理解小数做铺垫。)
二、数形结合,理解小数
1.实物表征,初步理解
师:1角=?元。
生:1角就是0.1元。
师:1角是0.1元,你是怎么想的?
生:1元=10角,1角=0.1元。
师:为什么?
生:1元里有10个1角,1角不够1元,它只是这10个1角中的一个。(师课件呈现)

生:1元=10角,相当于把1元平均分成10份,这1角就是10份中的1份,所以用0.1元表示。




