跨越断层,化零为整;数形结合,建构模型
骆乐
【课前思考】
现行人教版教材中三年级和五年级都编排了较多“解决问题”的内容,但四年级只安排了两个基本的数量关系教学内容(单价×数量=总价,速度×时间=路程)。而在五年级教学《简易方程》时,首先要求学生分析数量关系,然后根据数量关系列出方程,学生在解决稍复杂的问题时对一些数量关系就会分辨不清。追溯到四年级,我们发现在教学完这两个基本的数量关系之后,教材并没有安排相关内容进行巩固拓展,导致到了五年级学习方程时部分学生缺乏相关的经验积累。
两积之和结构的问题是小学阶段比重较大的问题,有很多经典问题就是以它为原型进行变式的(如鸡兔同笼等),但是两积之和问题在教材中并没有正式、独立的教学例题,只有一些零散的习题,学生碰到或许能解决,但却不能感受这些问题之间存在的联系。
基于这样的思考,我们设计了一节解决两积之和问题的课例。通过教学,让学生发现特征,提炼两积之和的模型,尝试借助模型去解决各种变式,同时在学习过程中感受用形去理解、表达题意和解决问题的好处,逐步渗透几何直观意识,培养几何直观能力,同时为后继的方程教学打下坚实的基础。
【教学目标】
1. 让学生从不同情境中提炼两积之和问题的特征,掌握解决两积之和问题的方法。
2. 经历观察、比较、归纳的过程,感受数与形之间的联系,提升解决变式问题的能力。
3. 在合作交流过程中,培养合作能力、归纳能力和几何直观能力。
【教学重点】能从不同的问题情境中发现两积之和的特征,掌握解决问题的方法。
【教学难点】引导学生沟通数与形之间的联系,借助形理解、解决各种变式问题。
【教学过程】
一、复习导入
1.列式解答
依次出示问题,学生口答,并说说是怎么思考的?

a.一副乒乓板20元,买5副需要多少元?
b.王叔叔开车从甲地到乙地,每小时行80千米,6小时到达。甲、乙两地相距多少千米?
c.工程队修路,每天修30米,10天修完,这条公路有多长?
2.整理数量关系
单价×数量=总价、速度×时间=路程、每天修的米数×天数=总长。
(设计意图:通过口答一步计算的问题,帮助学生回顾已经学过的简单数量关系,为后续教學做好铺垫。)
二、两积之和教学
1.出示问题,尝试解决
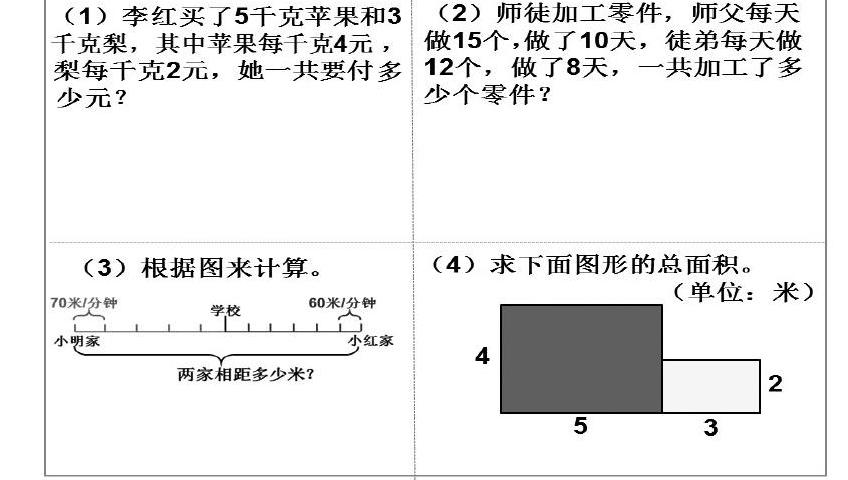
师(出示上图中题目):你们能解决吗?请在练习纸上完成。
(学生完成后集体进行校对)
师:在解决问题的时候你们是怎么想的呢?
生:我选第(1)题,苹果每千克4元,买5千克,用5×4=20(元)求出苹果的总价钱,梨每千克2元,买了3千克,用2×3=6(元)求出梨的总价钱,再相加就可以了。
生:我选第(4)题,先求红色长方形的面积是5×4=20(米2),黄色长方形的面积是3×2=6(米2),然后把两个加起来就是总面积。
……
根据学生回答,引出四个数量关系式:
苹果的价钱+梨的价钱=总价钱;师傅做的个数+徒弟做的个数=总个数;小明的路程+小红的路程=总路程;红长方形面积+黄长方形面积=总面积。
2. 对比交流,提炼特征
师:仔细观察这四道题,在解决方法上它们有没有什么相同的地方?
(学生讨论后反馈)
生:都是先算两部分,再把这两部分加起来。
生:都是先算乘法,再算加法。
师:是的,虽然题目不同,但都是先分别求两部分的积,再相加求和。这就是我们今天要学习的两积之和问题。
3. 沟通数与形之间的联系
师:除了解决方法是相同的,题与题之间还有相类似的地方吗?
生:我觉得第(1)(4)两题的算式是一样的。
师:除了算式一样,还有没有其他联系?
生:我觉得这道价格题能用这幅图表示,红色长方形面积相当于苹果的总价,黄色长方形面积就相当于梨的总价。
师追问:明明是长方形的面积呀,怎么能表示苹果和梨的总价呢?
生:图中的4可以表示苹果的单价4元,5表示苹果的数量5千克,2代表梨的单价,3代表梨的数量3千克。
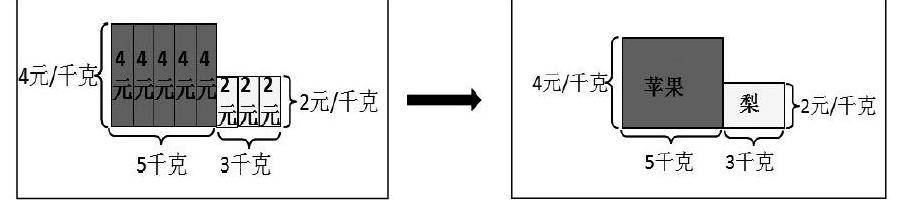
课件动态演示理解:
经过这个学生的启发,很多学生打开了思路:第(2)题能用第(3)题的图来表示,第(2)题能用第(4)题的图来表示……
师小结:同学们很善于观察思考,不仅发现这四道题有着相同的结构,还发现了文字与图形之间隐含的联系。接下去我们继续用你们的发现来解决问题。
(设计意图:通过四个不同情境问题的解决,让学生感悟解决方法上的共性,提炼两积之和问题的特征。同时引导学生进行数与形之间的沟通,深入感悟两积之和的模型。)
三、深化两积之和的模型
1.自主编题
师:刚才通过解决问题,我们知道第(1)题中李红共需要付26元,现在有五个信息了,你能将其中一个信息改成问题,重新编出一道题目吗?

出示编题要求(如上图)。先請一学生上来在电子白板上示范编。接着全班学生自主编题。
2.反馈编题
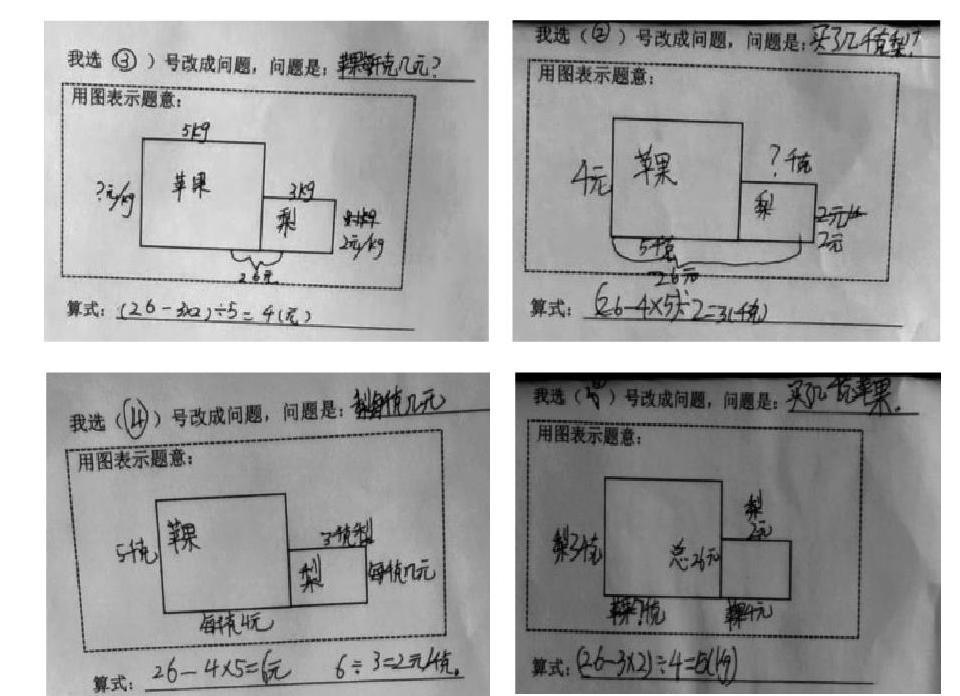
师:同学们很会动脑筋,编出了不同的题目,我们一起再来回顾一下。
3.对比沟通
师:观察一下,跟前面这些题相比,解决方法上有什么不同呢?
生:前面是先乘再加,后面是用总数减去其中一个部分得出结果。
生:前面是两部分相加,后面是用总数先减再除。
师:是的,其实还是利用这个关系,但当“和”已知时,要倒过来,用和减其中一个积,再利用之前学习的数量关系来解决题目中的问题。
(设计意图:通过对价格问题的逆向编题活动,不断让学生在条件与问题之间、数与形之间展开变式,渗透数形结合思想;同时对比正向和逆向题目的异同,让学生更深层次地感悟两积之和的模型,提升解决问题的能力。)
四、拓展两积之和的模型
1. 出示变式题
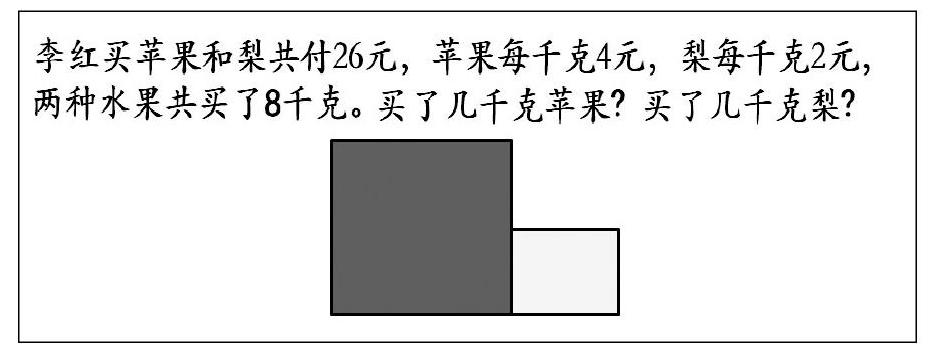
师:现在老师要把题目再变一变了,有两个问题,多了一个信息。这个问题能解决吗?还能用图来帮助我们分析吗?
(四人小组讨论,记录方法)
2. 交流方法
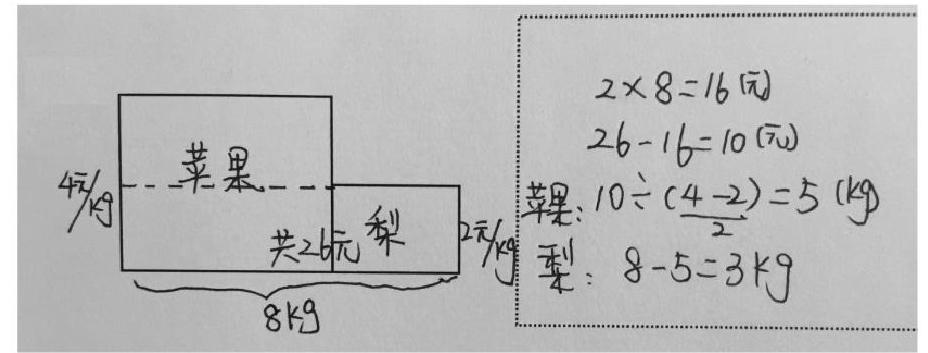
生:我加了一条辅助线(如上图),下面这个长方形表示的就是假设苹果的单价和梨一样,那8千克的水果只需要2×8=16元,而实际用了26元,说明苹果实际要多付26-16=10元,这是因为苹果实际每千克比梨贵4-2=2元,所以苹果有10÷2=5千克,梨就是8-5=3千克。
师:当苹果和梨的数量都不知道时,无法计算两部分的积,但像你们这样一分,就能知道下面这部分的积,然后就能求出上面这部分的积,这样就能求出苹果的重量和梨的重量。
3.小结提升
师:这样的问题你们以前有没有碰到过?
生:这是鸡兔同笼问题,我课外学习过,但是我没有用图形来解决。
生:我以前都是背公式的,现在发现用图形来解决更方便。
师:看来这幅图的作用可真大!
师:其实这个问题还有另外一种思考方法。
出示:
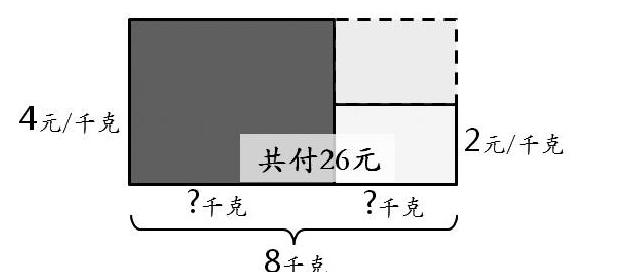
师:留给同学们课后思考!
(设计意图:借助图形解决复杂的两积之和问题,提高学生运用数形结合思想分析并解决复杂问题的能力,促进思维能力的发展。)
【教学反思】
一、不同情境找相同,感悟题组特征
教学前,笔者通过分析3~5年级的教材,提炼出了四种典型问题(价格问题、工作问题、路程问题、面积问题)作为例题进行教学,通过让学生自主解决和对比沟通,发现共性,从而提炼出两积之和的结构特征。让学生感悟到这些不同的问题竟然都是同一类问题,帮助学生跨越断层,化零散的知识点为整体的知识面。
二、正逆改编对比, 凸显模型本质
整节课的素材选取分为三个梯度,第一个梯度是正向的四道典型例题,第二个梯度是学生自主创编的四道逆向题,第三梯度是有两个未知量的拓展题。这三组素材层层递进,从简单的结构拓展变换成更复杂的结构。从不同的角度和宽度,丰富学生对两积之和这一模型的认知,让学生感悟到题型繁杂,千变万化,但万变不离其宗,都是两积之和的模型或变式。
三、沟通数形联系,深化模型理解
这四道题目的呈现有文字也有图形,意在让学生发现解决方法是相同之后,再次引导学生不断去寻找数与形之间以及形与形之间的联系,在不断求联的过程中,渗透数形结合思想。
在拓展练习中,引导学生尝试借助面积图去分析较难的问题,并给予充分思考和交流的时间,使学生深刻感受到借助图形来解决问题是非常不错的一种方法。事实上,学生通过这样的学习不仅感受到数与形之间的联系,更能借助形去理解难度更大的问题,能够主动去建构之前所学的一些内容和本课所学内容之间的联系。
(浙江省杭州市钱塘实验小学 310000)

