(2+1)维Kadomtsev-Petviashvili方程的留数对称及其相互作用解

葛楠楠,任晓静

(西北大学数学学院,陕西 西安710127)

1.引言

非线性演化方程及其精确解在物理、自然科学等领域有着极其重要的作用.在过去的几十年里,数学和物理领域在该方面取得了极大的进步.我们知道,对称群理论和Painlevé分析理论是发现和解决非线性演化方程的两大重要方法.在可积系统中,目前获取非局域对称的方法主要有递推算子法、逆递推算子法、Darboux 变换法、Bäcklund变换法、截断的Painlevé分析方法、Möbious变换法等[1−4].许多方程的相互作用解可以由非局域对称得到.最近,楼森岳教授发现在做非局域对称的Painlevé截断展开时发现,奇异流形的留数是一个非局域对称,称之为留数对称.而且,楼森岳教授通过Painlevé截断展开方法提出了相容的Riccati展式方法(CRE),该方法可以用来证明方程的CRE可解性,并根据此性质构造方程的新的相互作用解.尽管并不是所有的可积系统都是CRE 可解的,但是所有的CRE 可解方程都是可积的.CRE方法可以用于求解Kadomtsev-Petviashvili(KP)方程、sine-Gordon方程、Korteweg-de Vries(KdV)方程、非线性Schrödinger 方程等[5−17].

本文主要研究(2+1)维Kadomtsev-Petviashvili(KP)方程

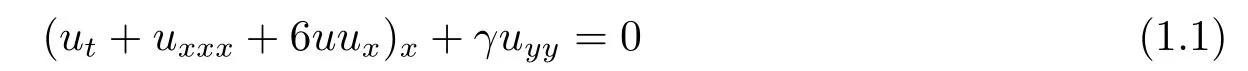
的非局域留数对称和CRE可解性及CTE可解性,并根据此性质构造(2+1)维KP方程的新的相互作用解.

2.非局域留数对称及其局域化

(2+1)维KP方程的Painlevé截断展开式可表示为如下的形式:

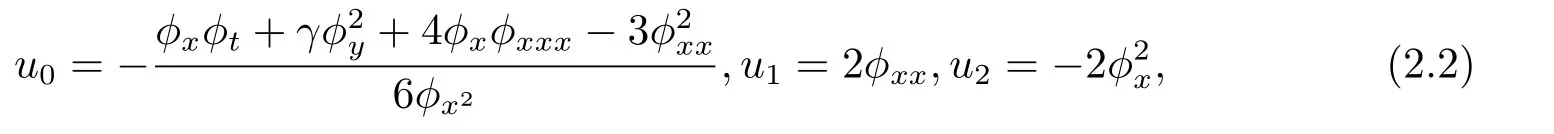
则

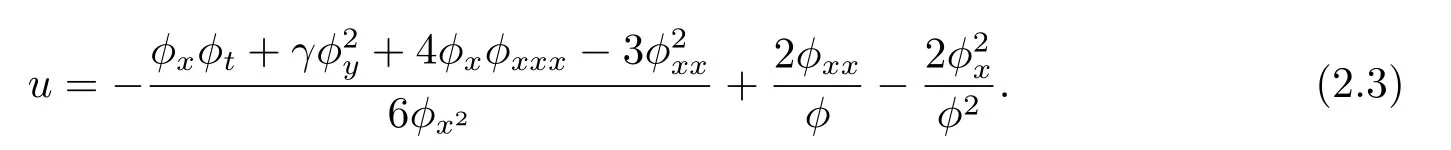
同时ϕ满足下面的Schwarzian形式:

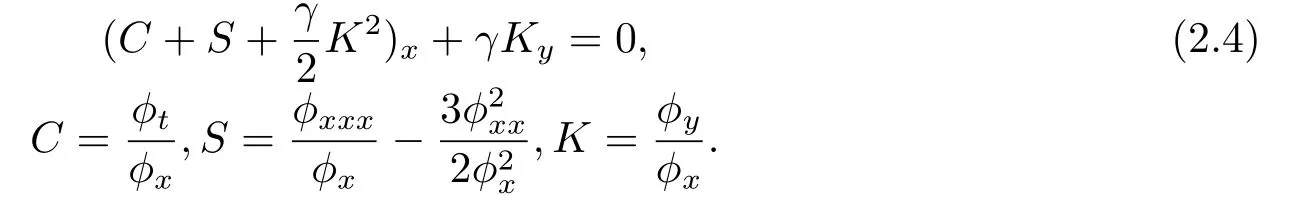
Schwarzian形式在下面的Möbious变换

下保持不变,即方程(2.4)容许三个对称σϕ=d1,σϕ=d2ϕ,σϕ=d3ϕ2,其中d1,d2,d3是任意常数.将表达式(2.1)代入方程(1.1)我们将得到下面的Bäcklund变换定理.

定理1(Bäcklund变换定理) 如果ϕ满足方程(2.4),则

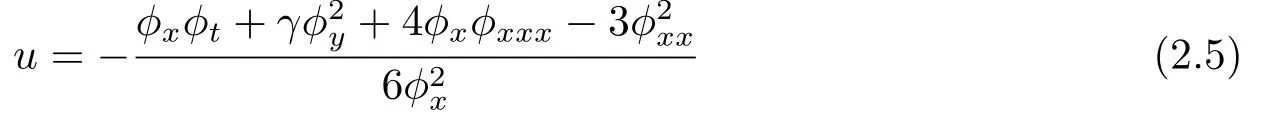
是方程(1.1)关于ϕ和解u间的一个Bäcklund变换,当ϕ和u满足Bäcklund变换(2.5)时,(2+1)维KP方程(1.1)有如下的留数对称

证将方程(2.5),(2.6)代入下面的表达式中

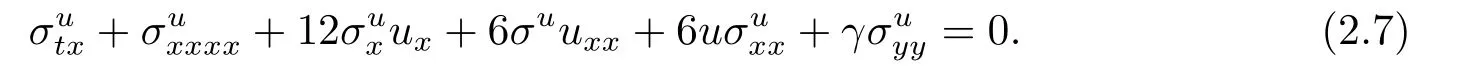
利用表达式(2.4)可以验证表达式(2.7)两端恒成立,而表达式(2.7)正好是方程(1.1)的对称方程,因此定理1得证.

由于非局域对称不能直接进行对称约化,因此需要将非局域对称局域化.为了寻求非局域留数对称的有限对称形式,我们需要解决下面的初值问题:

其中ε是群参数.受到函数(ε)及其导数的干扰,我们很难去解决初值问题(2.8),因此我们需要去延拓原方程使得非局域留数对称被转化为延拓的Lie点对称.通过引入新的变量g和h,利用表达式

方程(1.1)的非局域留数对称可被延拓为如下的Lie点对称:

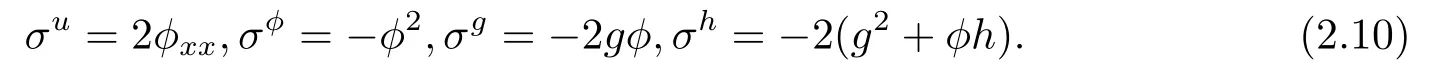
Lie点对称的向量场表示如下:

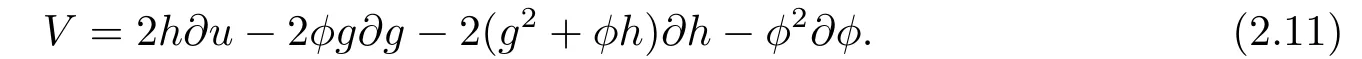
相应的初值问题(2.8)变成如下的初值问题

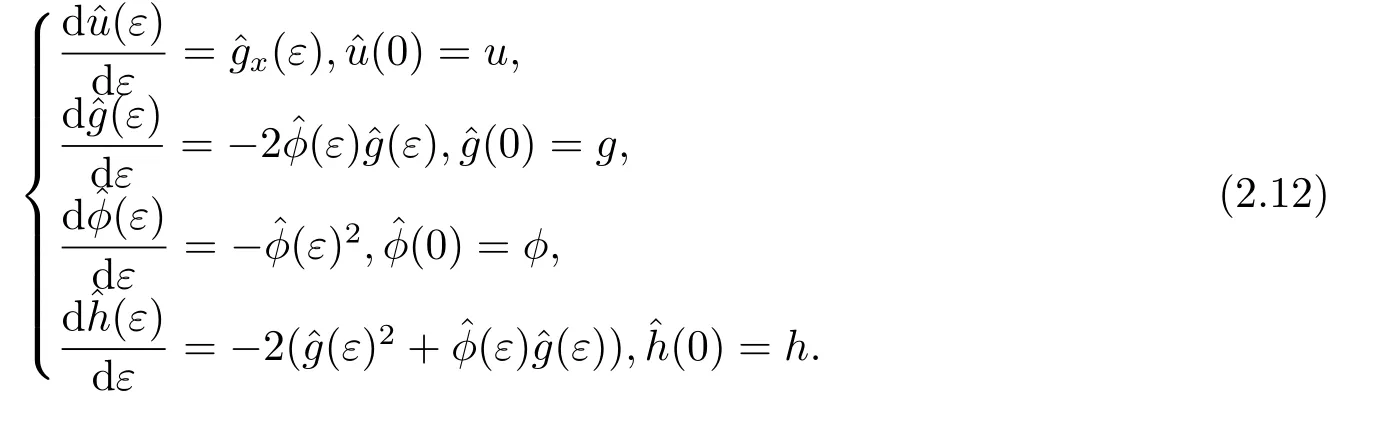
解上面的初值问题我们很容易得到下面的对称群变换定理.

定理2若{u,g,h,ϕ}是延拓系统(1.1),(2.4)和(2.9)的解,则也是他们的解,其中

注1通过定理2可知,从截断的Painlevé表达式得出的留数对称σu=2ϕxx正好是群(2.13)的无穷小形式.因为奇异流形系统(1.1),(2.4)和(2.9) 在变换

下是保持不变的,因此上面的群变换实际上等价于将表达式(2.2)代入(2.1)后的截断Painlevé展开式.

3.CRE可解和新的精确解

根据CRE方法,方程(1.1)有如下的截断展开形式:

其中ω=ω(x,y,t),R(ω)是Riccati方程

的解,a0,a1,a2是任意常数,γ=3.将表达式(3.1)和(3.2)代入方程(1.1),令R(ω)的各次幂前面的系数为零,可解出

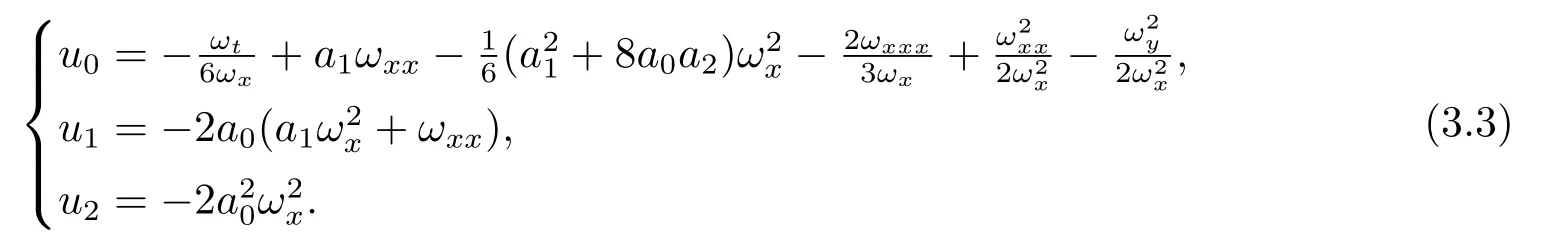
同时函数ω满足下面的方程

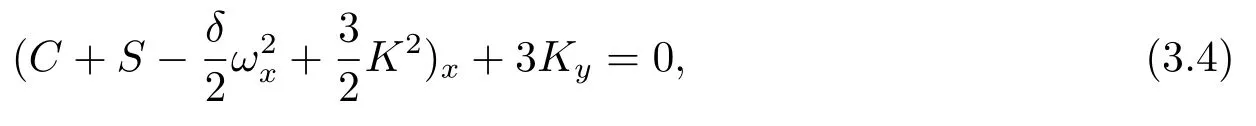
其中

根据CRE可解的定义可知,(2+1)维KP方程是CRE可解的.我们知道,当a0=1,a1=0,a2=−1时Riccati方程(3.2)有一个特解

此时,我们称CRE可解为CTE可解.显然,一个CRE可解系统一定是CTE可解的,反之亦然.此时,截断展开式(3.1)变为

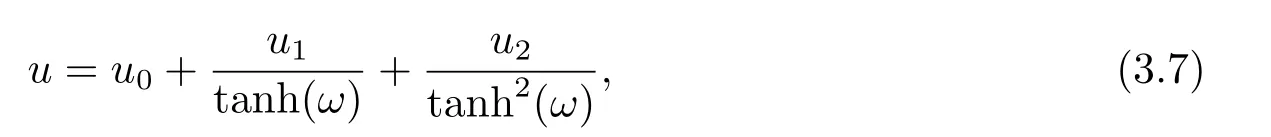
其中u0,u1,u2和ω由式(3.3)和(3.4)确定.因此有

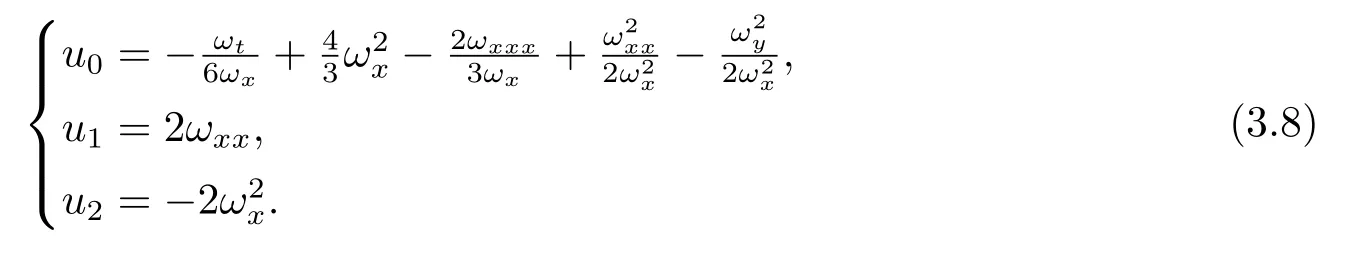
此时函数ω满足下面的方程

其中

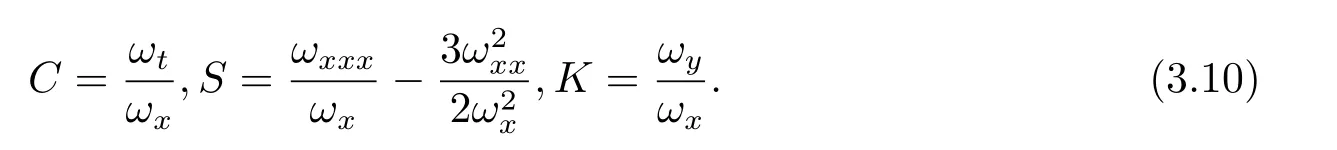
我们将得到如下的CTE可解定理.

定理3当a0=1,a1=0,a2=−1时,(2+1)维KP方程是CTE可解的,相容的tanh展式如下

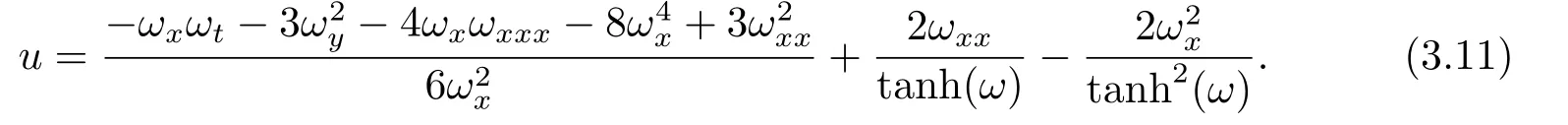
方程(1.1)的单孤子解是(3.9)式的直线解,由于(2+1)维KP方程(1.1)的CRE及CTE可解性,根据文[3],关于ω的方程(3.9)的解刻画了方程(1.1)孤立子和其他非线性激发模式的相互作用解,其一般形式为

把(3.12)代入(3.9)得到满足下面的椭圆函数方程

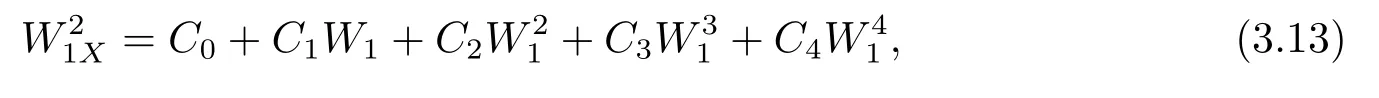
其中

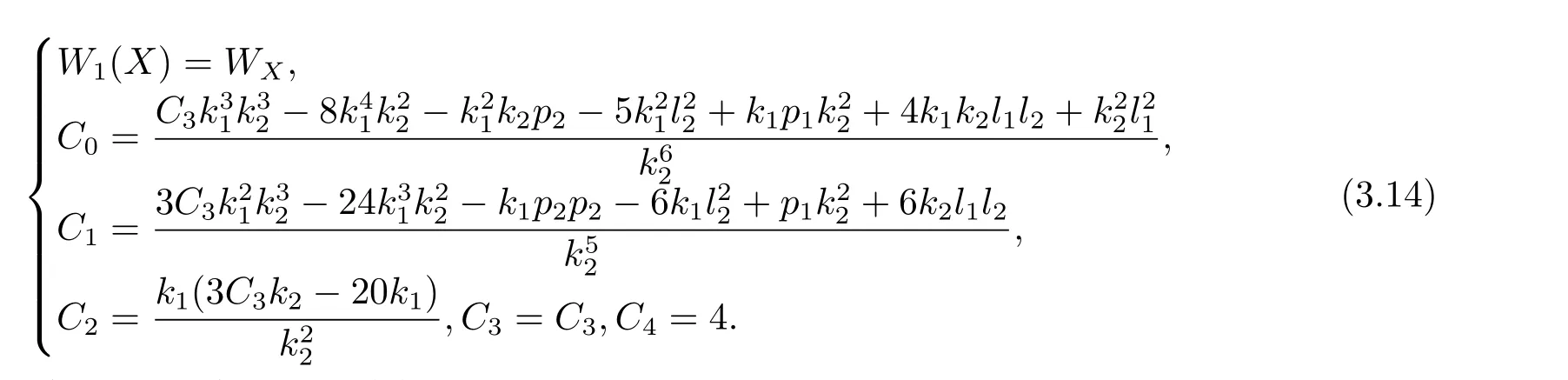
则(2+1)维KP方程有如下形式的解

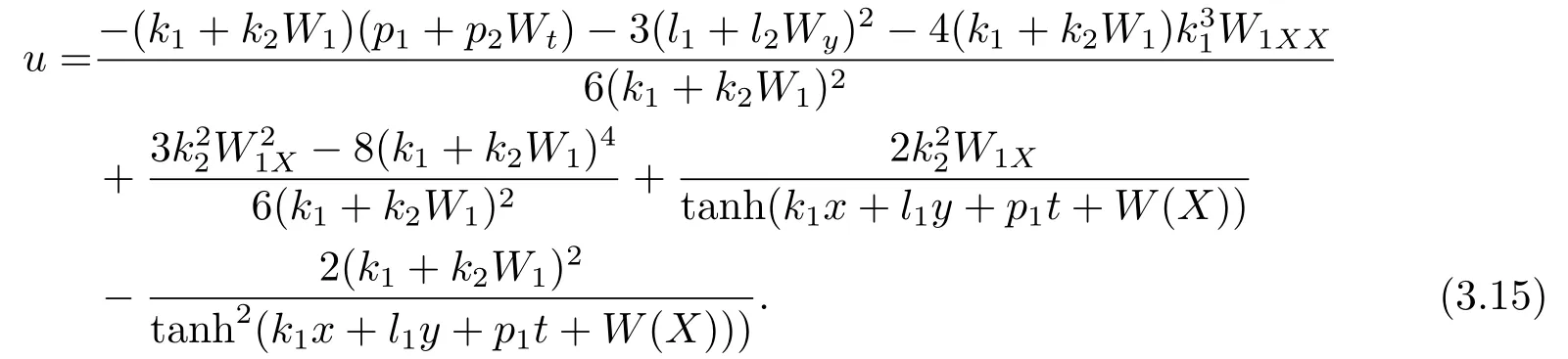
接下来我们将讨论两种特殊类型的相互作用解.

例1显然,方程(3.13)的一般解可以表示为雅可比椭圆函数.我们取ω为如下特殊形式的雅可比椭圆函数

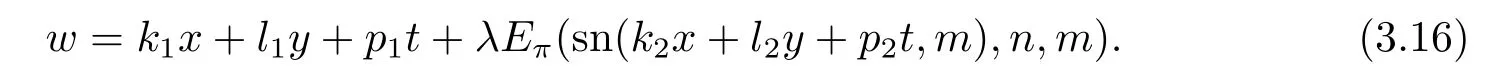
作为方程(3.9) 的解,表达式(3.15)刻画了方程(1.1)的孤立子与椭圆周期波的相互作用解,其中sn(q,m)为一般的雅克比椭圆sine 函数,Eπ是第三类不完全积分.把(3.16)代入(3.11),利用符号计算软件maple,我们得到方程(1.1)的孤立子与椭圆周期波的相互作用解

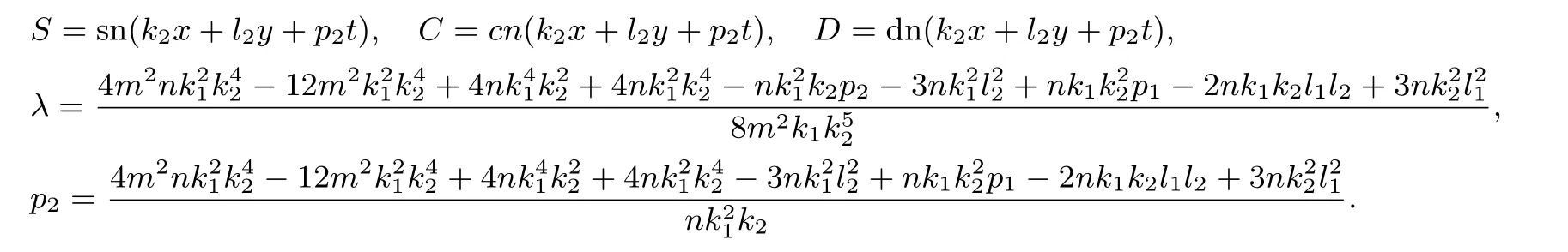
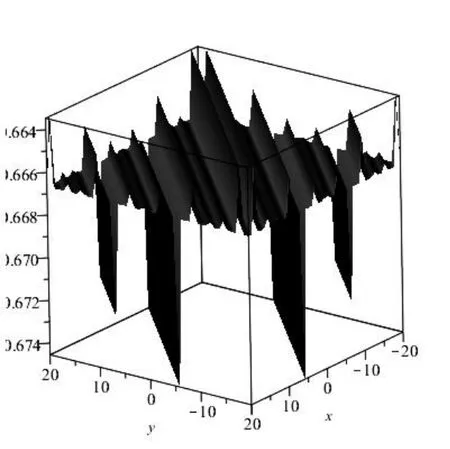
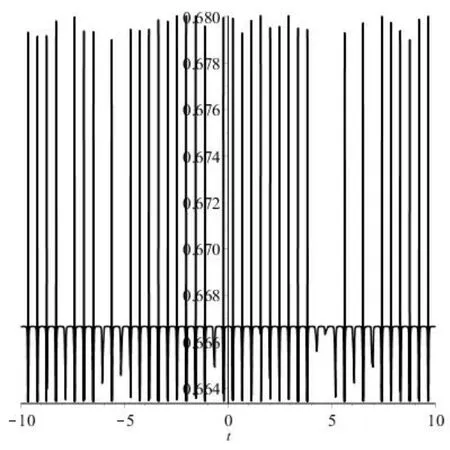
其中{k1,l1,p1,k2,l2,m,n}为任意常数,图(a1)描述的是当t=0时的方程的孤立子与椭圆周期波之间的相互作用解;图(a2)描述的是当x=0,y=0时u的平面周期波结构.其中参数选择选择如下:

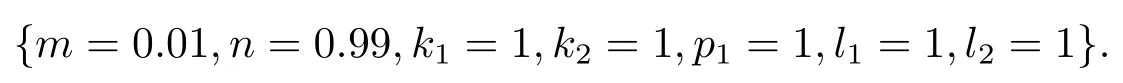
图(b1)描述的是当当t=0时的方程的孤立子与椭圆周期波之间的相互作用解;图(b2)描述的是当x=0,y=0时u的平面周期波结构.其中参数选择选择如下:

图(a1)

图(a2)

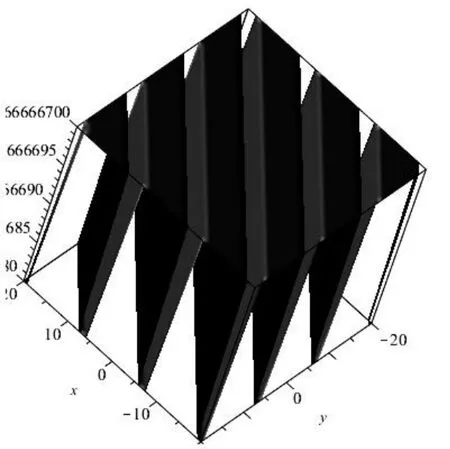
图(b1)

图(b2)

观察这些相互作用解的图形可以发现,在t=0时,对于不同的参数,方程的相互作用解不同,这些解具有多个不在同一平面上的波峰和波谷,且这些波峰和波谷的凹陷程度不同.

例2取W(X)=arctanh[sn(mX,n)],按照与例1类似的步骤可得方程(1.1)的相互作用解

其中{k1,l1,p1,l2,p2,m}为任意常数,

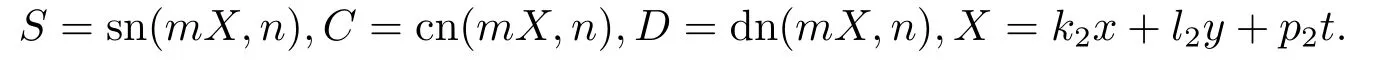
图(c1)描述的是当t=0时方程(1.1)的孤立波与椭圆周期波间的相互作用解;图(c2)描述的是当x=0,y=0时u的平面周期波结构.其中参数选择选择如下:

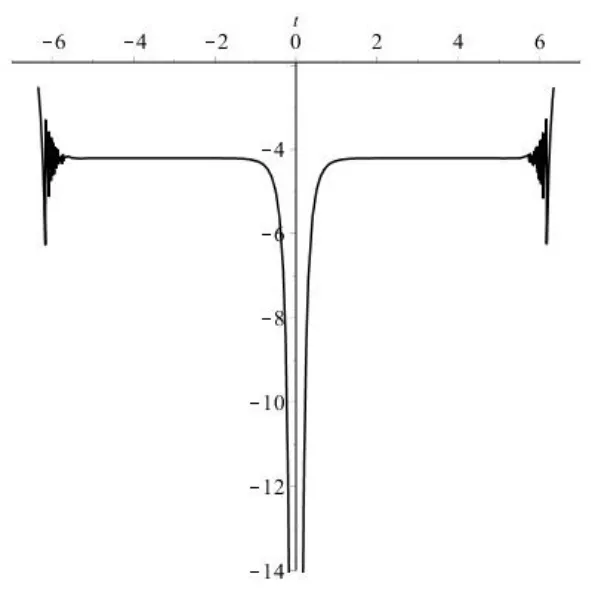
图(c2)

4.结束语

运用Painlevé截断展开方法,我们可以获得(2+1)维KP方程的非局域留数对称和Bäcklund变换定理.接着,我们将非局域留数对称局域化为(2+1)维KP方程的Lie点对称.利用Lie的第一基本定理研究了封闭系统的有限变换.由于(2+1)维KP方程具有CRE可解性,因此,CRE的一个特殊形式CTE方法被用于(2+1)维KP方程的求解.借助于CTE方法我们得到了(2+1)维KP方程的新的相互作用解,为了更好的研究解的性质,通过选取适当的参数,画出了上述解相应的图形.通过解的图形可以很好的描述(2+1)维KP 方程的相互作用解以及波峰、波谷的形状.