凸二次半定规划一个新的原始对偶路径跟踪算法

黎健玲,安婷,曾友芳,郑海艳

( 广西大学数学与信息科学学院,广西 南宁530004)

1.引言

本文考虑如下二次半定规划(简记为QSDP)

其中函数φ:Sn→Sn为自伴随线性算子,Sn表示n阶实对称矩阵空间.Ai(i=1,···,m),C和X都是n× n阶实对称矩阵,b∈Rm.表示矩阵的內积,即∀A∈Rp×q,B∈Rp×q,〈A,B〉=tr(ATB).X ≽0 和X ≻0 分别表示矩阵X是对称半正定矩阵和对称正定矩阵.

凸二次半定规划是半定规划[1−4]的推广,其在证券,金融,最优控制等领域中有着广泛的应用,因此对凸二次半定规划的研究受到学者们的关注,并已取得一批研究成果(见文[5–10]).文[5]提出了一个预估校正算法,该算法至多经次迭代可得到一个ϵ最优解.文[8]提出了一个非精确原始对偶路径跟踪算法.文[9]提出了一个基于参数核函数的原始-对偶内点算法.

受线性半定规划的HKM方向启发,本文提出一个基于HKM方向的新原始-对偶路径跟踪算法.在每次迭代中,算法通过求解一个线性方程组产生HKM搜索方向.在一定条件下证明了算法产生的迭代点列落在中心路径的邻域内,且算法至多经O(n|logϵ|) 次迭代可得到一个ϵ-最优解.

在一定的假设条件下,分析了该算法的迭代复杂度.

QSDP(1.1)的对偶问题(简记为QSDD)为

其中y∈Rm,Z∈Sn.

分别记QSDP(1.1)和QSDD(1.2)的可行域为FP和FD,并记F0P和F0D分别为FP和FD的严格内部,即

对于任意的可行点X和(X,y,Z),则对偶间隙为

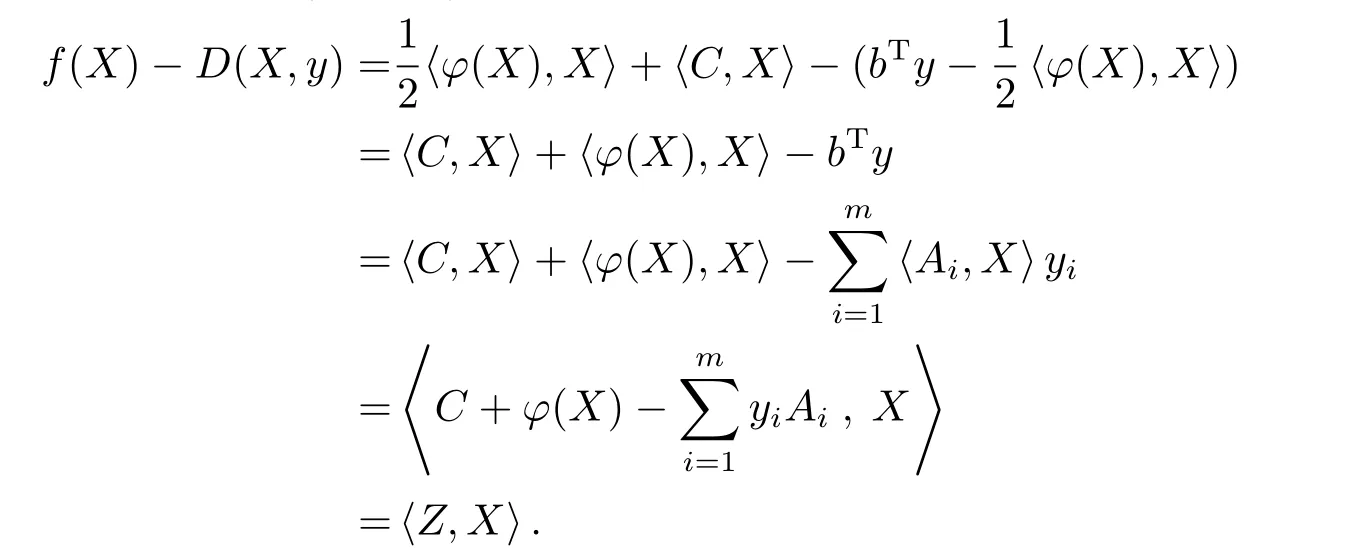
本文需作如下基本假设:

假设(A1) 线性算子φ(X)是对称半正定的,即满足

假设(A2) Slater约束规格成立,即存在X ≻0,Z ≻0,y∈Rm,使得X∈F0P,(X,y,Z)∈F0D;

假设(A3) 矩阵A1,A2,···,Am线性无关.

2.HKM 方向

称满足如下方程组

的点(X,y,Z) 构成的集合为中心路径,其中为中心参数,I为n阶单位矩阵.

设当前迭代点为(X,y,Z),且X∈F0P,(X,y,Z)∈F0D.用一步Newton 法求解方程组(2.1),得到下面方程组:

类似线性半定规划(见文[2]),HKM 搜索方向(∆X,∆y,∆Z)由下列线性方程组确定:

下面引理给出了线性方程组(2.3)的解(∆X,∆y,∆Z)的性质.

引理2.1假设(A1)-(A3)成立,X∈F0P,(X,y,Z)∈F0D,(∆X,∆y,∆Z)是线性方程组(2.3)的解,则下面结论成立:

证(i)根据方程(2.3b)和(2.3a)可得

其中最后一个不等式由假设(A1)得到.于是结论(i)成立.

(ii)由(2.3c)式得

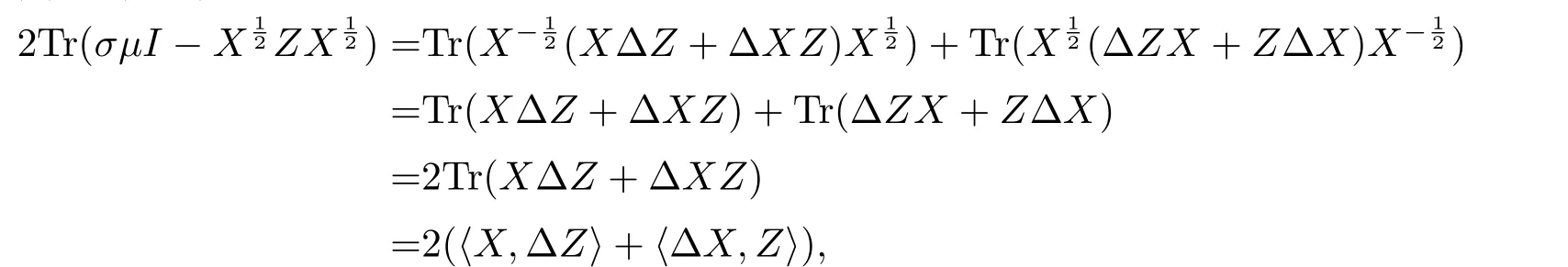
即结论(ii)成立.

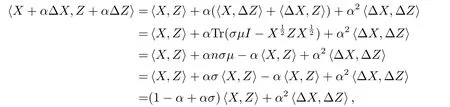
即结论(iii)成立.

3.长步原始对偶路径跟踪算法

本节将给出基于HKM方向(∆X,∆y,∆Z)的长步原始对偶路径跟踪算法的具体步骤,然后分析算法的性质.

算法3.1

步1 记(X,y,Z)=

步3 求解方程组(2.3),得到(∆X,∆y,∆Z);

步4 选择合适的步长α=αk≥0,令(Xk+1,yk+1,Zk+1)=(Xk,yk,Zk)+α(∆X,∆y,∆Z),k:=k+1,转回步1.

本文定义如下中心路径邻域:

在下面的讨论中,为简便起见,略去指标k,例:把(Xk,yk,Zk)简记为(X,y,Z).

引理3.1假设(A1)-(A3)成立,X∈F0P,(X,y,Z)∈F0D,(∆X,∆y,∆Z)是线性方程组(2.3)的解,对于任意给定的α>0,令

则

证对于任意给定的α>0,根据引理2.1(iii)及(3.3),有

因此,有

于是由(3.4)并结合(3.7),得

将上式进行化简并结合(2.3c),得

即(3.5)成立.

引理3.2假设(A1)-(A3)成立,(X,y,Z)∈NF(γ,Γ),(∆X,∆y,∆Z)是线性方程组(2.3)的解,则

其中µ(α)的定义见(3.3),且

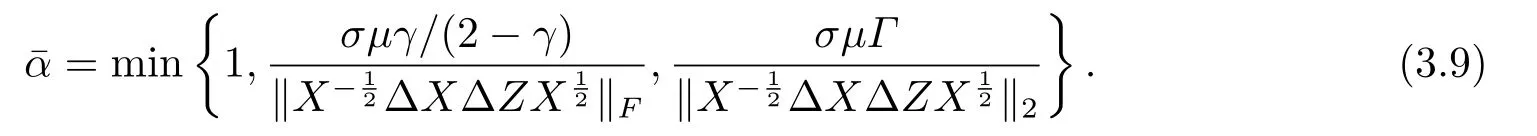
证由(X,y,Z)∈NF(γ,Γ)知

由(3.5)及λmax(·)为凸函数知

结合(3.10),(3.6),引理2.1(1)及文[2]中的引理3.1 可得

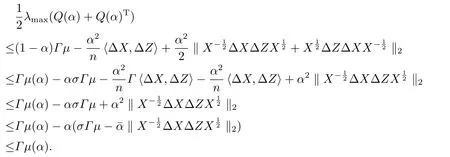
最后一个不等式源自(3.9).由此可知(3.8)式右边不等式成立.

同理,由(X,y,Z)∈NF(γ,Γ)知

由(3.5)及λmin(·)是凹函数知

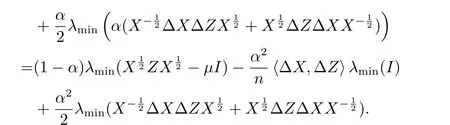
结合(3.11),(3.6)及文[2]的引理3.1 可得

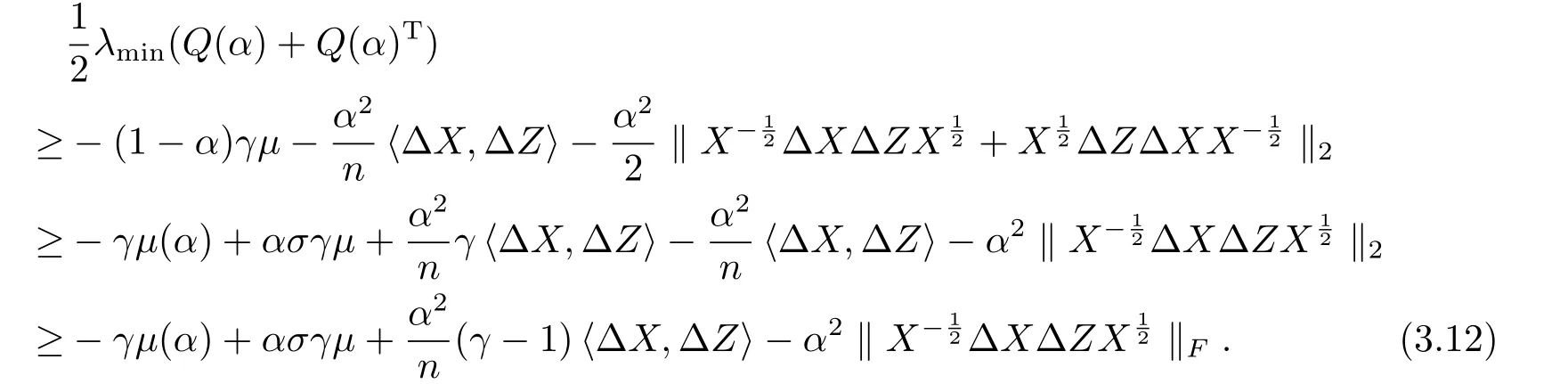
由‖·‖F的定义得

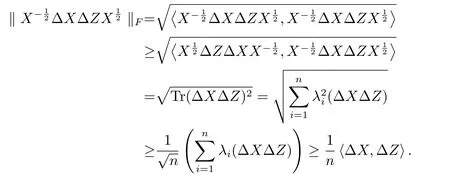
最后一个不等式源自(3.9).因此,(3.8)左边不等式成立.

综上可知本引理成立.

引理3.3假设(A1)-(A3)成立,(X,y,Z)∈NF(γ,Γ),(∆X,∆y,∆Z)是线性方程组(2.3)的解,则对于任意的α∈(0,),有(X(α),y(α),Z(α))∈NF(γ,Γ),其中

证先证明X(α)∈根据(2.3a)且X∈F0P,有〈Ai,X(α)〉=bi,i=1,···,m.由(3.13)及α <知α于是进而X(α)=因此X(α)∈F0P.

令

则易知N(α)非奇异,且N(α)E(α)N(α)−1=Q(α).根据文[2]的引理3.3 有

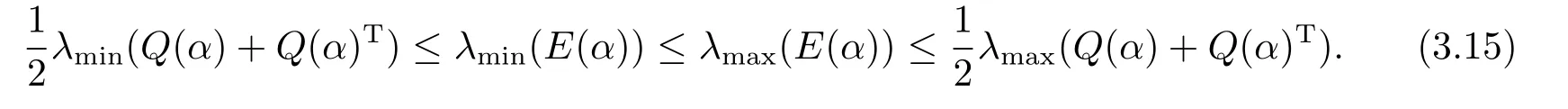
由(3.9)和(3.13)知≤,于是结合(3.8)和(3.15),得

将(3.14)的第二式代入上述左边不等式,得

于是,有

故

类似可得

于是

下面证明(X(α),y(α),Z(α))∈F0D.根据(3.16),设γ∈[0,1),得

由此可知X(α)Z(α)≻0,结合X(α)≻0 即知Z(α)≻0.由(X,y,Z)∈F0D及(2.3b)知

因此,(X(α),y(α),Z(α))∈F0D.

综合以上证明即知(X(α),y(α),Z(α))∈NF(γ,Γ).

引理3.4假设(A1)-(A3)成立,X∈F0P,(X,y,Z)∈F0D,(∆X,∆y,∆Z) 是线性方程组(2.3) 的解,则

证证明中需用到以下两个不等式(见文[11]):

从而

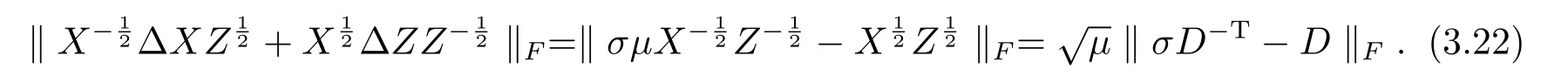
根据矩阵F-范数的定义和矩阵內积的性质有

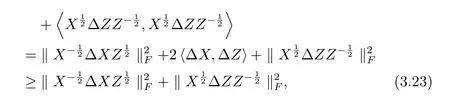
其中最后一个不等式是利用了引理2.1(1).于是由(3.22)和(3.23)即得

且

即(3.17)成立.

根据(3.21),(3.17)及矩阵D的定义,得

即(3.18)成立.

根据(3.21),(3.24)及矩阵D的定义,得

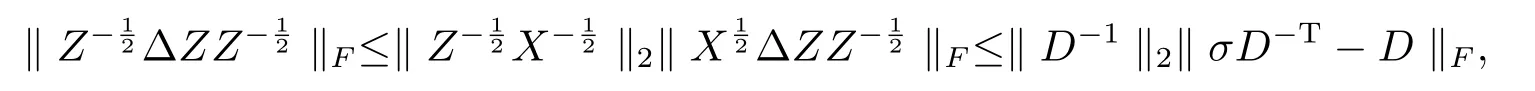
即(3.19)成立.

由(3.21),(3.19)及矩阵D的定义,得

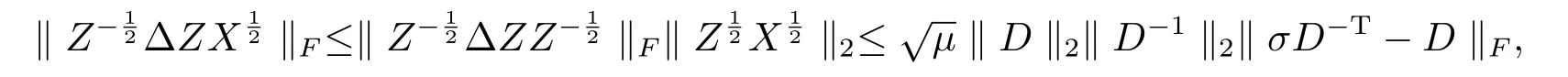
即(3.20)成立.

参照文[2]的引理5.7,可得如下结论:

引理3.5设矩阵W非奇异且则对于任意的有

下面定理给出了算法3.1 的一次迭代后迭代点(X(α),y(α),Z(α))的性质.

定理3.1假设(A1)-(A3)成立,(X,y,Z)∈NF(γ,Γ),Γ≥γ,(∆X,∆y,∆Z)是线性方程组(2.3)的解.令

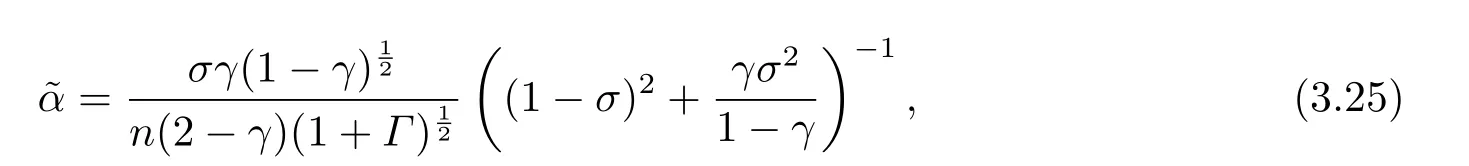
则对于任意的α∈[0,],有

证根据引理3.3,我们只需证明≤,即证

和

根据(3.28)和引理3.5,得

根据(3.17),(3.20),(3.27)-(3.29),有

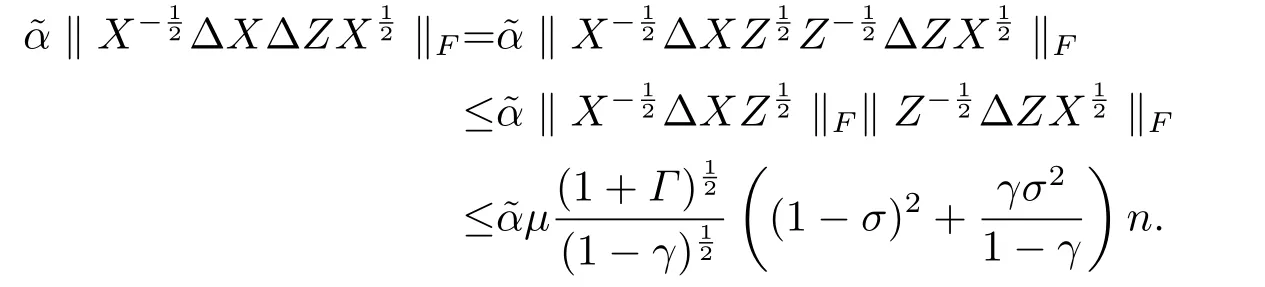
将(3.25)代入上式,即得

根据(3.18),(3.28),(3.29)和(3.25),可得

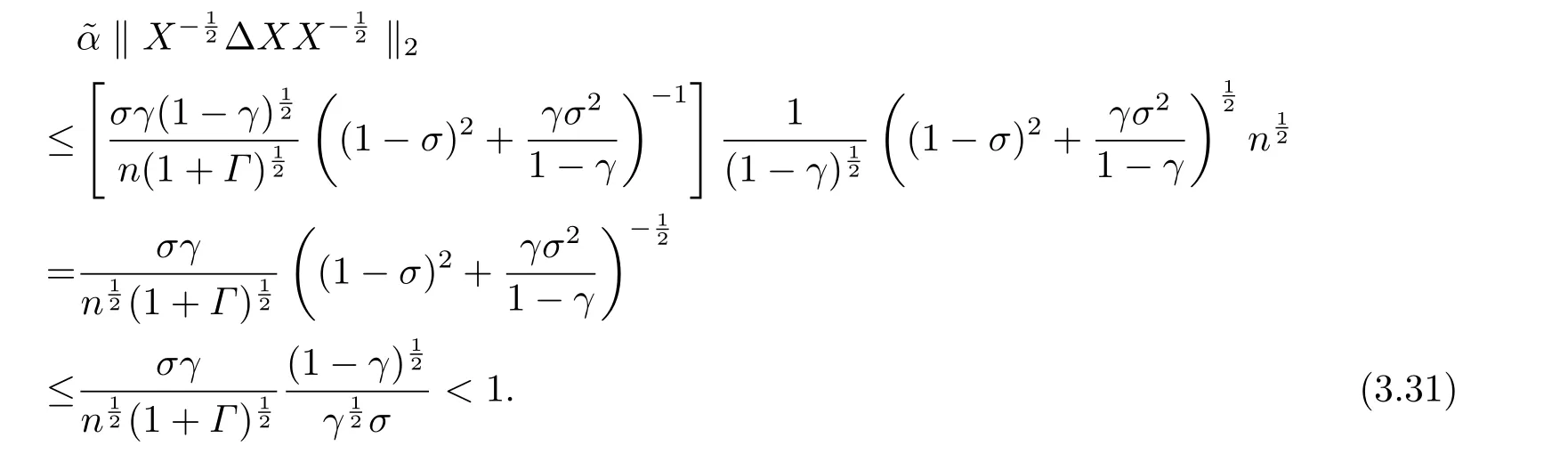
综合(3.30)-(3.32)即知不等式(3.26)成立.

基于定理3.1,算法3.1 中步长αk的选取方法如下:对于任意的k≥0,取

下面分析证明算法3.1 的迭代复杂度,为此需作如下进一步假设:

假设(A4)满足不等式:

定理3.2假设(A1)-(A4)成立,对于任意的ϵ>0,算法3.1 至多经次迭代可得到一个ϵ-最优解,其中

证根据(2.4)及假设(A4),有

根据定理3.1和(3.33)得αk≥τ/(1−2σ),代入上式,即得

于是有

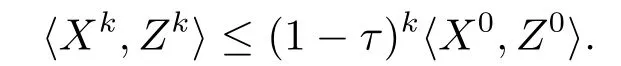
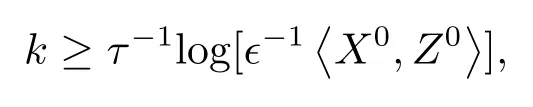
因此结论成立.