基于Pena距离的双重广义线性模型的统计诊断

邢伊琦,吴刘仓,聂兴锋

(昆明理工大学理学院,云南 昆明650093)

1.引言

经典的线性模型可以描述许多研究领域的现象,但是,在生物、医学、保险等领域的研究人员发现,经典的线性模型会遇到很多方法上的困难,在此基础上,广义线性模型也就应运而生了.广义线性模型是经典线性模型的推广.1972年Nelder和Wedderburn首先提出广义线性模型[1],McCullagh和Nelder在1983年出版了系统论述此专题的专著《Generalized Linear Models》.在一些经济领域和工业产品质量改进中,对均值和方差同时建模是非常有必要的,所以双重广义线性模型近年来引起了许多学者的关注.1984年,Pregibon在文章中首先提出了对散度参数建模的广义线性模型[2];WANG和ZHANG[3]研究了双重广义线性模型中仅均值模型的变量选择;WU和LI[4]研究了逆高斯分布下联合均值和散度模型的变量选择;陈海露[5]研究了双重广义线性模型的参数估计与变量选择;吴刘仓等[6]研究了基于Box-Cox变换下联合均值与散度广义线性模型的极大似然估计;胡江等[7]研究了基于Pena距离的广义线性回归模型的影响分析等.

在响应变量分布未知但已知其前两阶矩存在的情况下,Wedderburn提出了拟似然方法来进行参数估计.拟似然的方法是假定总体前两阶矩阵存在,然后通过对其对数似然方程求极值得到参数的估计值.陈希孺[8]在广义线性模型中对拟似然方法有详细的阐述;吴刘仓等[9]研究了缺失数据下双重广义线性模型的参数估计;袁巧莉等[10]研究了混合双重广义线性模型的参数估计等.

我们知道,统计诊断在数据分析中占有举足轻重的地位,主要目的就是找出数据中的异常点或强影响点,常用的统计量有似然距离、Cook距离等,Pena距离[11]这一诊断统计量是美国统计学教授Daniel Pena在2005年首次提出的,并对其在线性模型上的影响分析做了详细的研究,这种方法与之前的方法有较大差别,之前的方法是研究删除一(组)点,对回归分析的影响以及对预测值的影响,或者是某个(组)样本点的微小扰动对参数估计的影响或是对模型预测的影响.而Pena距离这一统计量则是研究的是样本中的某一个(组)点受其余各个(组)点的影响,简单来说,就是样本中各点删除后,对某一特定的点的回归值或预测值的影响.本文基于Pena距离,采用伪似然和扩展拟似然的方法估计参数,并通过数据删除模型的参数估计和统计诊断,比较了删除模型和未删除模型对应的统计量之间的差异.通过Monte Carlo模拟验证,本文提出方法的有效性.最后,通过实例研究,表明本文所提出的模型和方法是实用可行的.

2.双重广义线性模型下的极大似然估计

我们先给出双重广义线性模型(Double Generalized Linear Model,DGLM)为:

其中yi为被解释变量,xi=(xi1,xi2,...,xip)T,zi=(zi1,zi2,...,zip)T为解释变量,β=(β1,β2,...,βp)T为均值模型中的未知参数,γ=(γ1,γ2,...,γp)T为散度模型中的未知参数.xi,zi两个解释变量可能完全相同,部分相同或者完全不同,但相同的解释变量在均值模型和方差模型中有不同的影响方式.g(µi)=xTi β是均值模型,h(ϕi)=zTi γ是散度模型,g(·)和h(·)是联系函数,V(·)是关于均值的方差函数.

定理2.1对于模型(2.1),其Pena距离为:

证根据文[11],我们定义Pena距离如下:

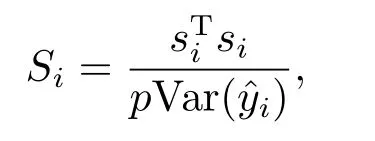
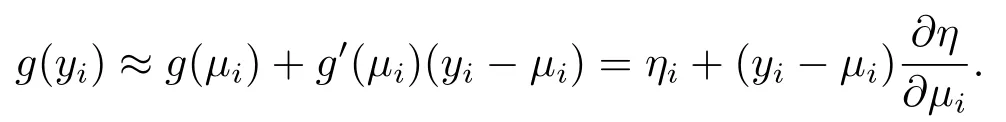
对上式两边求方差，有：

上述两式相减,得：

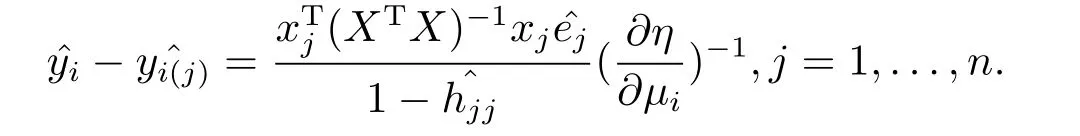
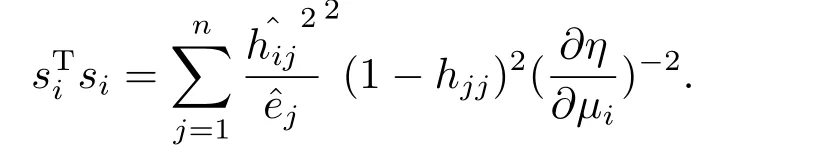
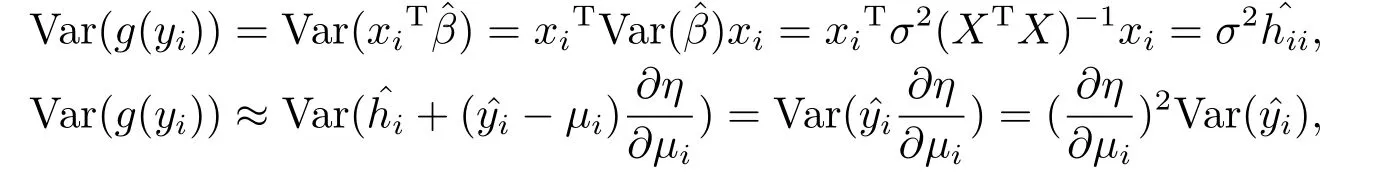
故

故Pena距离为：

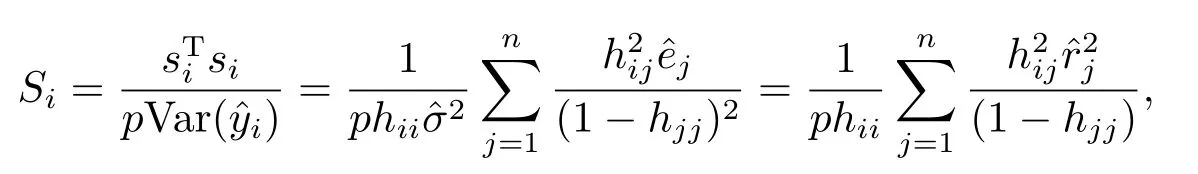
3.双重广义线性模型的统计诊断

数据删除是统计诊断中最常用的也是最基本的方法之一,比较删除第i个点前后模型参数估计量之间的差异,能得出一些的结论.用这些结论,我们能评价我们估计方法的好坏,详细内容参考韦博成[12]等的文献或书刊.模型(2.1)的数据删除模型可表示为：

对于未删除模型(2.1)和删除模型(3.1),为检验第i个数据点在整个数据集中是否为异常点或强影响点,可通过比较删除第i个点前后统计推断结果的变化,看出这个点是否为异常点或者强影响点,而统计推断结果的变化可由统计推断量来得到.

对于一组随机变量y1,y2,···,yn的分布是未知的,但知道其期望和方差存在,期望我们用E(y)表示,那么方差为:

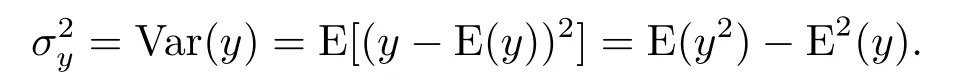
从式中,我们知道E(y)是一阶原点矩,Var(y)是二阶中心矩,我们也可以认为方差是二阶原点矩减去期望的平方.对于本文选用的模型,我们选用扩展拟似然算法和伪似然算法来进行我们的参数估计.本文采用的扩展拟似然函数(EQL)Q+为：

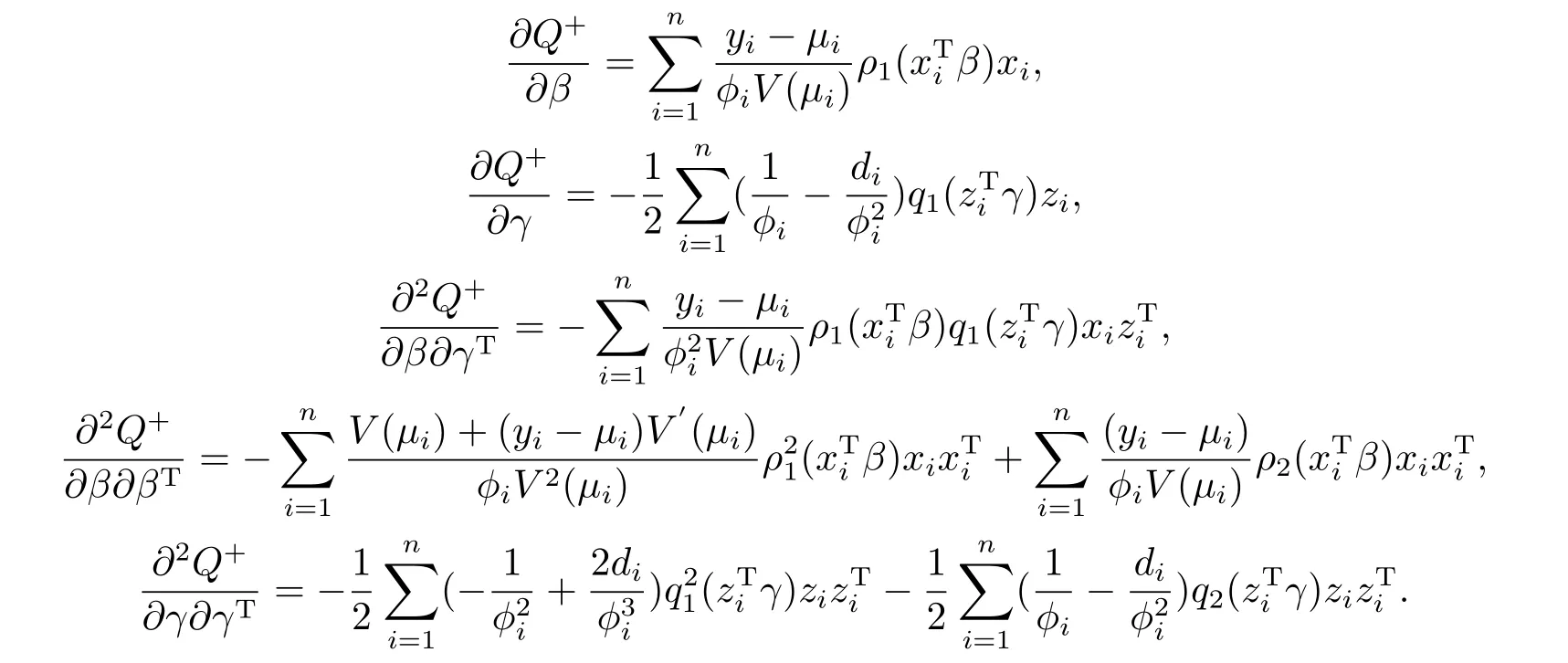
本文中采用的伪似然函数(PL)Qp为:

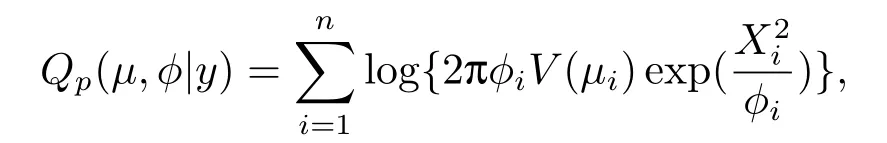
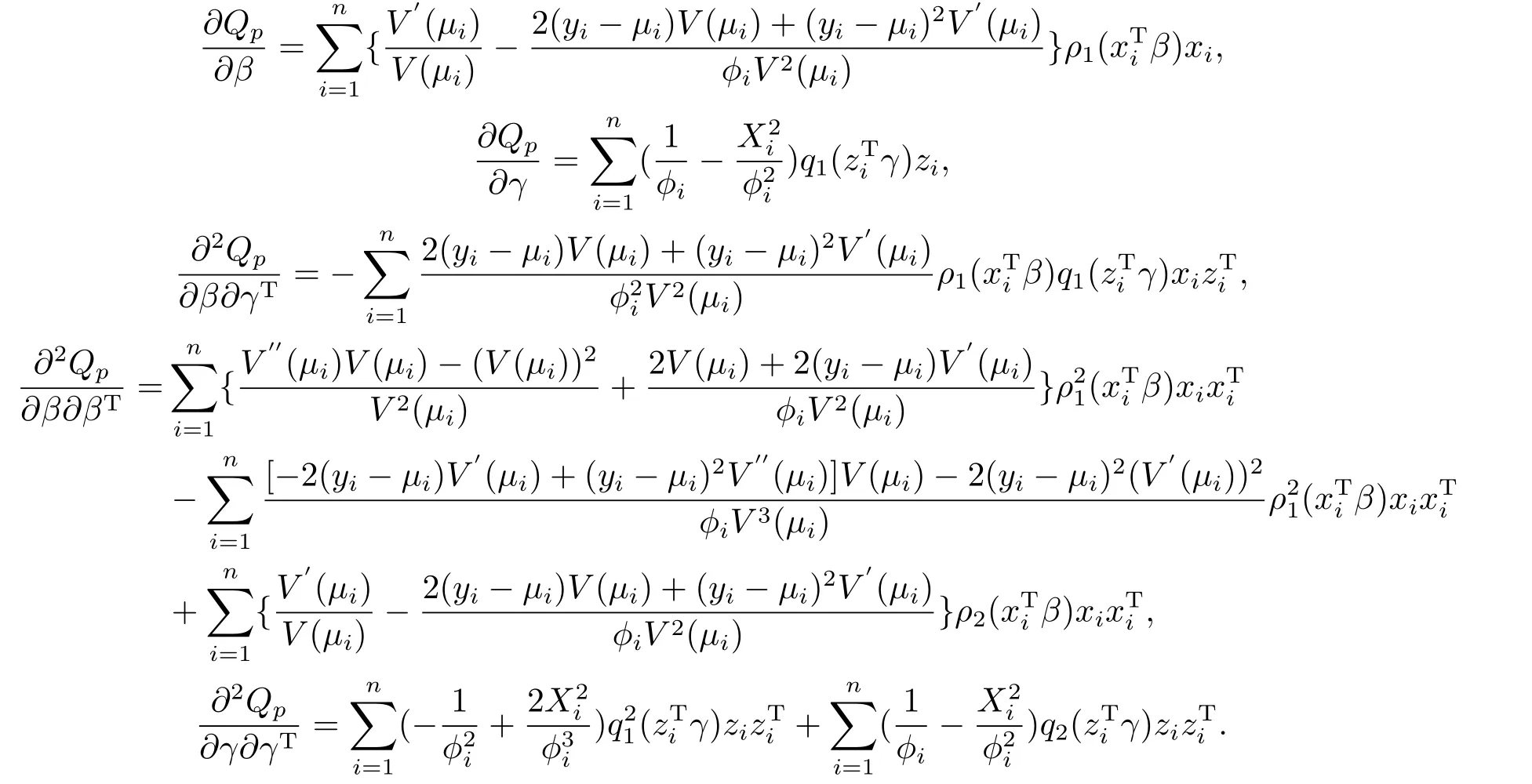
用Gauss-Newton迭代法可得到参数极大似然估计的估计值.设未删除模型的参数估计值用,表示,则删除模型的参数估计值用,表示,则有=(,)T.

由Gauss-Newton迭代法可得到参数极大似然估计的估计值和,但如果解释变量的维数为二维或者高于二维，这时参数和均为向量,难以比较大小.这时我们就可以用Cook距离来刻画参数的变化,Cook距离定义如下:

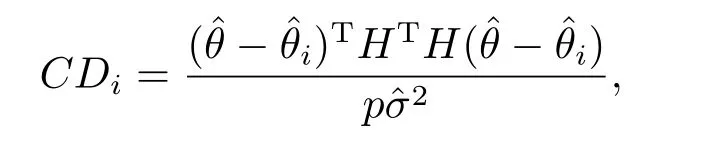
其中H=(xT,zT)T为解释变量,p为对应解释变量的维数,为未删除模型方差的估计值.

在分析具体数据时,先计算出各点的Cook距离,通过画散点图,找出其中特别大的Di,对应数据点可能就是异常点或强影响点.

Pena距离与Cook距离相比较，前者研究的是删除一个(组)点后对估计值或预测值的影响,而后者则研究的是样本中的某一点受其余各点的影响,简单的说,就是研究样本中各点删除后,对某一特定的点的估计值或预测值的影响,Pena距离定义如下：

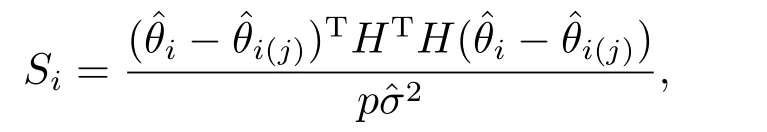
其中H=X(XTX)−1XT称为帽子矩阵,p为相应解释变量的维数,为删除第i个点后模型方差的估计值.是删除第j个点后第i个点的参数估计值.具体分析时,同样是先算出删除各点后某一点的Si,画出散点图,其中Si较大的就可能是异常点或强影响点.

4.Monte Carlo模拟

为了比较Pena距离和Cook距离的诊断效果,本文我们采用Extra-Poisson模型进行模拟.Extra-Poisson 模型如下

根据模型(4.1)产生模拟数据,其中yi是根据双重广义回归模型产生的相互独立的响应变量,解释变量xi和zi相互独立产生于U(0,1).给定β0和γ0的真值分别为β0=(0,1,1)T,γ0=(0,1,1)T.将第170号,190 号样本点的被解释变量的值做改变,即从样本点中人为的制造两个异常点,然后应用本文研究的Pena距离以及Cook 距离进行诊断,根据异常点的诊断情况来判断本文提出的方法是否行之有效.模拟结果如图1-4所示：

从图中我们可以看出,无论是用PL或者EQL方法,第170号点以及190号点均被诊断出来了,这说明本文提出的方法是可行并且有效的,下面用具体的实例进一步说明.

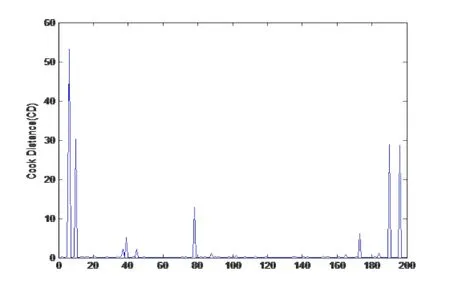
图1 PL的Cook距离CD散点图

图2 PL的Pena距离PD散点图

图3 EQL的Cook距离CD散点图

图4 EQL的Pena距离PD散点图

5.实例分析

这里我们用一组检验某种工业用发动机性能试验的数据,该试验使用的原料是柴油和从有机原料中通过蒸馏产生的气体的混合物,在各种不同的速度x(计量单位：百转/分钟)下，测量发动机的马力y.

表1 发动机性能数据

我们建立模型

利用伪似然和扩展拟似然的估计方法得到的参数做统计诊断，得到图5-8的结果.

图5 发动机性能数据PL的Cook距离CD散点图

图6 发动机性能数据PL的Pena距离PD散点图

图7 发动机性能数据EQL的Cook距离CD散点图

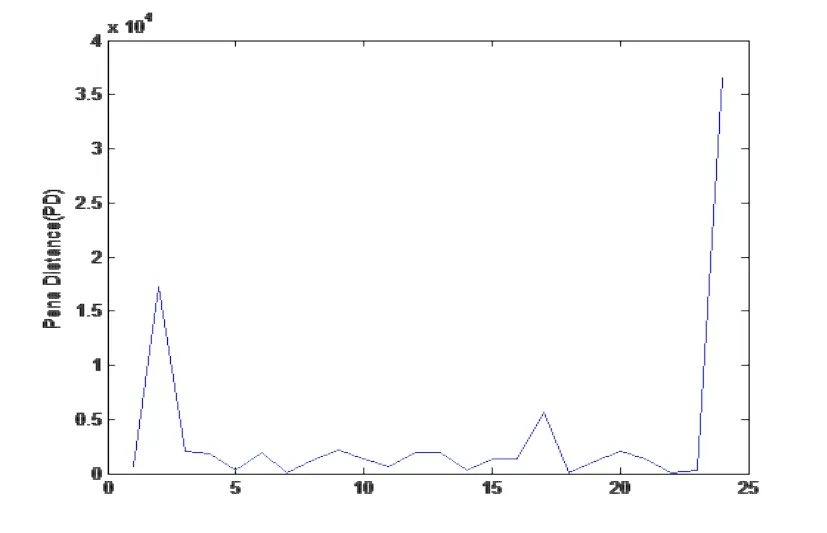
图8 发动机性能数据EQL的Pena距离PD散点图

从图5-8的结果可以看出,用伪似然和扩展拟似然的方法估计参数做统计诊断的效果大致相同.我们以图5和图6用伪似然的方法估计的参数做的统计诊断为例,由图5可知第2号点、16号点和24号点可能为异常点或强影响点,由图6可知第2号点和24号点可能为异常点或强影响点.由文[12]中的例5.4 可知,第2、24号点为异常点或强影响点,比起Cook距离,Pena距离很好地诊断出了这个点.

6.结论

本文针对分布未知但其一阶矩和二阶矩存在的随机变量,建立了双重广义线性模型,运用扩展拟似然和伪似然方法进行参数估计再用Pena距离和Cook距离进行统计诊断,得到在一定的条件下Pena距离优于Cook距离的结论.最后,通过Monte Carlo模拟和实例研究的结果验证,说明了本文所提出的模型与方法的有效性和实用性.