Poisson-Geometric模型下时间一致的最优再保险-投资策略选择

杨鹏,杨志江,孔祥鑫

(1.西京学院理学院,陕西 西安710123;2.西安交通大学数学与统计学院,陕西 西安710049;3.潍坊市工程技师学院电气系,山东 诸城262233;4.诸城市密州路学校,山东 诸城262233)

1.引言

1952年美国经济学家Markowitz在文[1]中引入了投资组合策略选择问题,他用财富的均值表示投资者的收益,用财富的方差表示投资者的风险.投资组合策略选择问题的目标是:求得最优策略使投资者的收益最大,同时投资者面临的风险最小.自从该问题提出,就受到了很多学者的关注,特别是进入21世纪,有越来越多的学者研究该问题.文[2]首次研究了多阶段、连续时间的投资组合策略选择问题;文[3]用线性二次控制的方法研究了投资组合策略选择问题;文[4]研究了负债对投资策略的影响.

对保险公司来说,通过投资可以增加财富,因此,有很多学者研究保险公司的投资策略选择问题.如:文[5]在第二章第四节研究了Cramer-Lundberg(CL)经典风险模型下,再保险-投资策略选择问题,通过求解相应的Hamilton-Jacobi-Bellman(HJB)方程得到了最优策略和有效前沿的显式解问题;文[6]在文[5]的基础上,研究了复合Poisson-Geometric(PG)风险模型的再保险-投资策略选择问题;文[7]在风险资产满足CEV模型时,利用线性二次控制理论研究了再保险-投资策略选择.

上述提到的文献,得到的最优策略是时间不一致的.在保险实务中,保险人每天的偏好有可能是不同的,但是在很多情形下,他们追求的最优策略基本保持一致.因此,研究时间一致的策略在保险实务中具有很重要的现实意义.文[8]在CL经典风险模型下,研究了时间一致的再保险-投资策略选择问题;文[9]在Heston模型下,研究了时间一致的再保险-投资策略选择;文[10]在风险资产带跳下,研究了时间一致的再保险-投资策略选择问题;文[11]在CEV模型下,研究了时间一致的再保险-投资策略选择问题;文[12]在状态相依下,研究了时间一致的策略选择问题.

PG风险模型是近年来发展起来的一个模型,它是经典CL风险模型的推广.CL风险模型中,风险事件与赔付事件是等价的,而且描述理赔次数的是Poisson过程.正如文[13]所说,在保险实务中,风险事件与赔付事件有可能不是等价的,比如在保险公司推出免赔额制度和无赔款折扣(NCD)等制度后,风险事件就不一定是赔付事件,理赔次数过程就不再是Poisson过程.PG风险模型中,描述理赔次数的过程是PG过程.文[14]通过研究得到:PG过程是Poisson过程的推广,并且PG过程中风险事件与赔付事件不再等价.文[15]研究了PG风险模型中,最优投资-分红策略;文[16]在比例再保险和超额损失再保险下,研究了PG风险模型中的调节系数方程、破产概率等问题;文[17]研究了一类PG风险模型的预警区域的矩母函数.

据我们所知,在PG风险模型中,没有学者研究时间一致的再保险-投资策略选择问题.因此,本文在PG风险模型中研究了时间一致的再保险-投资策略选择问题.大多数学者在考虑再保险时,一般采用期望值原理计算,本文按照方差值原理计算再保险的保费.方差值原理是期望值原理的推广,方差值原理不但含有理赔额的期望,还含有理赔额的二阶矩.在考虑投资时,风险资产满足带跳的随机微分方程.应用随机控制理论,我们求得了时间一致的再保险-投资策略和最优值函数的显式解,分析了结果的经济意义及模型参数对最优策略的影响.

2.金融模型与研究目标

为了引入PG保险模型,首先给出PG分布和PG过程的定义.

定义2.1(PG分布) 设常数λ >0和0≤l <1,t >0,若随机变量X的概率母函数为则称X服从参数为λ和l的PG分布,记为X∼PG(λ,l).

定义2.2(PG过程) 若计数过程{N(t),t≥0}满足条件:(i)N(0)=0;(ii)N(t)具有独立平稳增量;(iii)对t≥0有N(t)∼PG(λt,l),则称{N(t),t≥0}是参数为λ和l的PG过程.

注2.1(i)通过PG过程的定义有,

(ii)当l=0时,PG 过程转化为Poisson过程,所以PG过程可看作Poisson过程的推广.

注2.2(i) 若{N(t),t≥0}是Poisson过程,即l=0,则E[N(t)]=Var[N(t)]=λt,λ代表了保单的平均风险暴露.当风险事件与理赔事件一致时,λ也是平均理赔频率.因此,当每一次风险事件发生都理赔且每一次理赔确实反映一次风险事件时,理赔次数可以用Poisson过程描述.

(ii) 如果保险公司附加一些理赔条件(如:免赔额或NCD理赔条件)时,理赔事件就不等同于风险事件了,这时就不能用Poisson过程描述理赔次数.对于PG过程,当l≠0时E[N(t)]≠Var[N(t)],因此可以用PG过程描述理赔事件不等同于风险事件的情形.

基于上述定义的PG过程,下面在CL经典风险模型的基础上,给出PG风险模型.设X(t)为时刻t保险公司的财富,它满足微分方程dX(t)=cdt−dS(t).其中c >0是保险公司单位时间的保费收入;这里{Yk,k=1,2,···}是一列相互独立同分布取值为正值的随机变量序列,它们的共同分布为FY(y),密度函数为fY(y).Yk表示第k次理赔额,具有有限的一阶矩µ11和二阶矩µ12.{N1(t),t≥0}是PG过程,代表到时刻t为止保险公司理赔发生的次数,它具有参数λ1>0和0≤l<1.

再保险是保险公司规避风险的一种方式,再保险主要有比例再保险和超额损失再保险两种形式,本文考虑比例再保险.对任意的时间t >0设比例再保险的水平为a(t),满足a(t)≥0,当a(t)∈[0,1],表示保险公司进行再保险;当a(t)>1表示保险公司采取了新业务,或者理解为保险公司接受了新的分保,这时保险公司充当了再保险人的角色.大多数文献在考虑再保险的保费计算方式时使用期望值原理计算,然而期望值原理只包含理赔的一阶矩(期望)但不包含理赔的其它信息.方差值原理是计算再保险保费的另一种方式,方差值原理不但包含理赔的一阶矩(期望)也包含理赔的二阶矩,方差值原理是期望值原理的一种推广.基于此考虑,本文使用方差值原理计算再保险的保费,也就是再保险的保费为其中α>0为一常数.考虑比例再保险后,保险公司的财富过程满足下面的随机微分方程

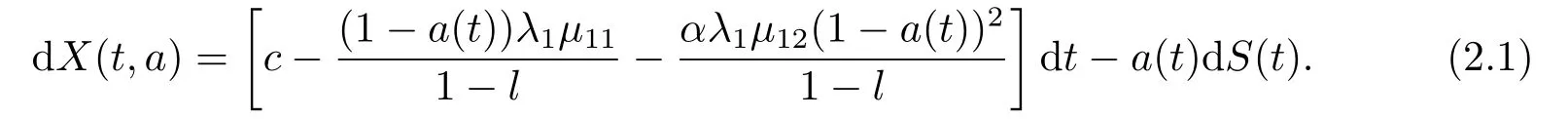
在金融市场上投资是保险公司增加收入的一种方式,下面给出本文用到的金融市场.金融市场由一个无风险资产(如债券、银行存款等)和一个风险资产(如:股票等)组成.无风险资产的价格为B(t),满足微分方程dB(t)=rB(t)dt,其中r >0表示利率.在现实金融活动中,由于受到一些不确定因素的影响(如:金融危机、政府宏观调控、通货膨胀、负债等),风险资产会发生一些剧烈的跳动,因此本文假设风险资产价格满足带跳的随机微分方程.也就是,风险资产的价格P(t) 满足下面带跳的的随机微分方程

其中µ >0为常数,表示风险资产的平均收益率;σ >0也是常数,表示风险资产的波动率;{W(t),t≥0}是一标准布朗运动,代表不确定的收益或损失;是一复合泊松过程,代表风险资产发生的跳动,它满足其中{N2(t),t≥0}是参数为λ2的泊松过程;{Zk,k=1,2,···}为一列独立同分布的随机变量序列,共同分布为FZ(z),密度函数为fZ(z).Zk的一阶矩和二阶矩都存在,分别为µ21和µ22.由于保险公司从风险资产上获得的平均收益一般要大于从无风险资产上获得的平均收益,因此假设µ >r.另外还假设{Yk,k=1,2,···},{N1(t),t≥0},{Zk,k=1,2,···}和{N2(t),t≥0}相互独立.

设T为投资的终止时刻,保险公司在有限的时间区间[0,T]内进行再保险来减少风险,同时考虑在金融市场上进行投资来增加财富.设π(t)是时刻t保险公司在风险资产上投资的资金,剩余的资金全部投资在无风险资产上.在时刻t保险公司选取再保险策略a(t)和投资策略π(t)作为控制变量,记u(t)=(a(t),π(t)).同时考虑比例再保险和投资后,保险公司的财富过程为X(t,u),满足下面的随机微分方程

这里X(0,u)=x0.

设Ft是由布朗运动W(t)生成的右连续且完备的流,它对应的完备概率空间为(Ω,Ft,P),其中Ω为样本空间,P为概率测度.

定义2.3(可行策略) 再保险-投资策略u(t)=(a(t),π(t))称为可行策略,如果它满足条件:(i)a(t)和π(t)关于流Ft是循序可测的,且是右连续的、左极限存在;(ii)a(t)≥0且满足所有可行的再保险-投资策略记为U.

在以往基于再保险-投资的最优策略研究中,大多数学者研究了下面的最优化问题

其中E0,x0=E[·|X(0,u)=x0];γ >0为常数表示保险人的风险厌恶程度.文[9]指出问题(2.3)是时间不一致的,也就是在不同的时间保险人选择的最优策略是不同的.问题(2.3)是时间不一致的原因是因为问题(2.3)中包含了条件方差,详细的证明读者可以查阅参考文[18],这里不再进一步阐述.人们的偏好可能会随着时间的改变而改变,然而大多数情况下人们希望最优策略在不同的时间是一致的.时间一致策略更精确的表述是:对于某固定的时刻s,若求得最优策略u(·)使得问题(2.3)成立;那么对于之后的时刻t,该策略u(·)仍是问题(2.3)的最优策略.

和其它一些文献如文[9]等类似的,本文研究如下的目标函数

这里(t,x)∈[0,T]×R,Et,x=E[·|X(t,u)=x],γ为常数表示保险人的风险厌恶程度.下面给出平衡策略的定义.

定义2.4(平衡策略) 对于任意的初始状态(t,x)∈[0,T]×R和可行策略u∗(t),选择三个实数0,R 和ζ >0,定义如下的策略:

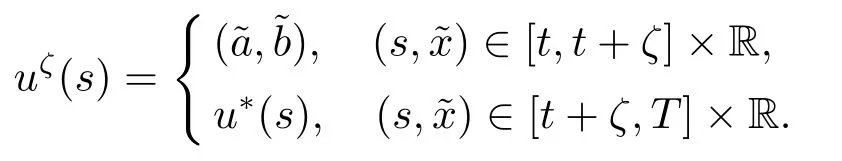
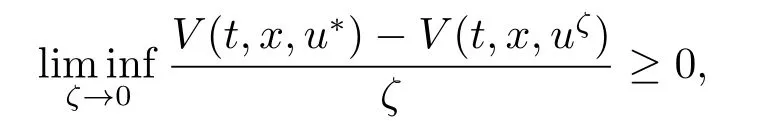
则u∗(t)称为平衡策略,相应的平衡值函数为V(t,x)=V(t,x,u∗).

文[9]证明了上述定义的平衡策略等于时间一致的策略,通常的最优值函数等于平衡值函数.所以接下来,对于平衡策略和平衡值函数,我们就分别称其为最优时间一致的策略和最优值函数.

3.主要结果

本节对于财富过程(2.2),利用随机控制理论求解时间一致的最优策略和最优值函数,本节是本文的主要研究结果.与文[12]中的定理2.1类似,我们给出如下的检验定理:

定理3.1(检验定理) 设F(t,x),G(t,x),H(t,x)定义在[0,T]×R上,它们关于t连续可微,关于x二阶连续可微;也就是F,G,H∈C1,2.若F,G,H满足如下的HJB方程

则

u∗(t)=(a∗(t),π∗(t))是时间一致的最优策略.

本定理的证明类似于文[12]中的定理2.1,因此本文不再给出证明.从(2.4)式和定理3.1,可得

因此

综合考虑财富过程满足的方程和边界条件F(T,x)=x,G(T,x)=x,与文[9]和[14]等文献类似,设F(t,x)和G(t,x)分别满足如下式子:

可得F(t,x)和G(t,x)的偏导数如下:

把(3.6)-(3.8)以及上面的各偏导数,代入(3.1)式化简后得

由一阶最优性条件,得到最优再保险策略和最优投资策略分别满足下式

把(3.10)式和(3.11)式分别代入(3.9)式和(3.2)式,可得

因此,求解(3.12)式和(3.13)式,只需求解下列常微分方程.

解(3.14)式和(3.16)式,得A(t)=m(t)=er(T−t).A(t)和m(t)分别代入(3.15)式和(3.17)式,求得B(t)和n(t)如下

在上述讨论的基础上,可得下面的定理:

定理3.2对于财富过程(2.2),最优的时间一致的再保险策略为

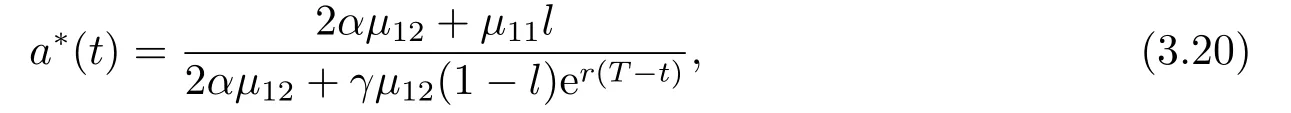
最优的时间一致的投资策略为

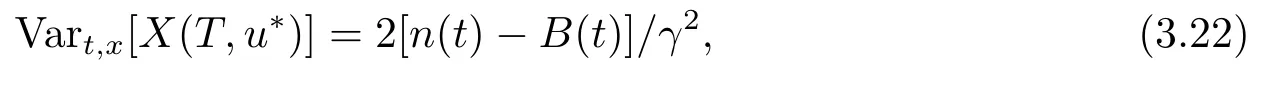
在最优策略和终止时刻T下,财富过程的方差为这里B(t)和n(t)分别满足(3.18)式和(3.19)式.

注3.1从定理3.2可得,Et,x[X(T,u∗)]=er(T−t)+B(t)/γ+0.5γVart,x[X(T,u∗)],该式给出了风险和收益的关系,当投资者面临风险Vart,x[X(T,u∗)],获得的收益满足上式.

注3.2从定理3.2可以参到,最优再保险策略不依赖于风险资产中的参数;最优投资策略,不依赖于保险市场中的参数.这是因为,我们假设再保险市场和风险资产市场是相互独立的.

4.经济意义及敏感性分析

本节分析上一节中得到的结果的经济意义,并通过数值计算分析一些模型参数对最优再保险-投资策略的影响.

Ⅰ最优再保险策略

(3.20)式关于γ求偏导数,得到

可见,最优再保险策略a∗(t)是关于参数γ单调递减.γ代表保险人的风险厌恶程度,保险实务中保险人一般都是厌恶风险的,因此随着风险的增大,自然会把风险转移给再保险者.(3.20)式关于r求偏导数,得到

因此,最优再保险策略a∗(t)关于r单调递减,这是符合实际的.因为这里r为无风险资产的利率,当无风险资产的利率增加时,保险人将从金融市场上获得更多的收益.因此,在每次理赔中希望承担更小的风险,把风险转移给再保险者.

接下来通过数值算例,给出参数α和l对最优再保险策略的影响.假设理赔额服从参数为1的指数分布,即fY(y)=e−y,y≥0;则µ11=1,µ11=2.因此,最优再保险策略为

例4.1设t=2,r=0.05,l=0.2,γ=0.05,T=4,6,8,10,α∈[0.02,0.08].图4.1给出了α和T对最优再保险策略的影响.

图4.1 α和T对最优再保险策略a∗(t)的影响

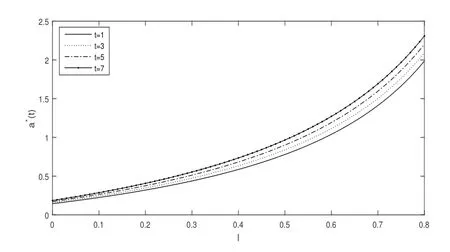
图4.2 l和t对最优再保险策略a∗(t)的影响

结果分析:从图4.1中可以看到,最优再保险策略关于α单调增加,关于T单调递减.随着α的增加,再保险的保费增加,保险人的再保险比例增大;随投资终止时刻的延长,保险人将减少再保险比例.

例4.2设T=8,r=0.05,α=0.06,γ=0.05,t=1,3,5,7,l∈[0,0.8].图4.2给出了l和t对最优再保险策略的影响.

结果分析:从图4.2中可以看出,最优再保险策略关于参数l和t是单调增加.当l=0,即PG风险模型为经典CL风险模型时,再保险的比例最小;随着投资终止时刻的到来,保险人会增加再保险的比例.

Ⅱ最优投资策略

(3.21)式关于µ求偏导数,有

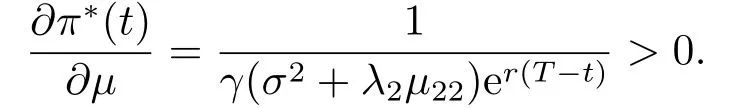
从上式可以看出,最优投资策略π∗(t)关于µ单调递增.这里µ是风险资产的平均收益率,平均收益率增加,保险人自然会把更多的财富投资到风险资产.(3.21)式关于γ求偏导数,得到

因此,最优投资策略π∗(t)关于γ单调递减,这是符合实际的.γ是风险厌恶参数,投资者一般都是厌恶风险的,随着风险的增大,投资者自然会把更多的资金投资到无风险资产.(3.21)式关于σ求偏导数,有

从上式,可以得出最优投资策略π∗(t)关于σ单调递减.σ表示风险资产的波动率,波动变大说明风险增大,保险会把更多的资金投资到无风险资产.

下面通过数值计算分析其它模型参数最优投资策略的影响.因为风险资产在发生跳跃时,可以向正的方向跳跃也可以向负的方向跳跃,因此设ZK的共同密度函数fZ(z)为双指数分布,即当z≥0时fZ(z)=pη1e−zη1,当z <0时fZ(z)=qη2ezη2.这里p≥0,q≥0,分别表示风险资产向正向跳跃和向负向跳跃的概率,满足p+q=1,η1>0,η2>0.所以µ21=p/η1−q/η2,µ22=2p/(η1)2+2q/(η2)2.因此,最优投资策略变为

例4.3设T=6,r=0.05,µ=0.1,γ=0.05,η1=1,η2=2,λ2=0.3,σ=0.2,t=1,3,5,7,p∈[0.3,0.8].图4.3给出了p和t对最优投资策略的影响.

图4.3 p和t对最优投资策略π∗(t)的影响

图4.4 r和λ2对最优投资策略π∗(t)的影响

结果分析:从图4.3看出,最优投资策略π∗(t)关于参数p单调递增,关于t单调递减.参数p代表风险资产向正向跳跃的概率,p越大说明从风险资产获得的期望收益会增加.因此,在风险资产上投资的资金会增加.t代表投资时刻,随着投资时刻接近投资的终止时刻,保险人将减少在风险资产上投资的资金.

例4.4设T=4,t=2,r=0.05,µ=0.1,γ=0.05,η1=1,η2=2,σ=0.2,p=0.4,q=0.6,λ2=0.2,0.4,0.6,0.8,r∈[0.01,0.09].图4.4给出了r和λ2对最优投资策略的影响.

结果分析:从图4.4可以看出,最优投资策略π∗(t)关于r和λ2都是单调递减.r表示无风险资产的利率,随着无风险资产的利率增加,保险人在无风险资产上的收益会增加.因此,在风险资产上投资的资金会减少.λ2代表单位时间内风险资产跳跃的次数,越大说明风险资产的风险越大,风险增大保险人将减少在风险资产上投资的资金.

5.总结

本文在PG风险模型中,研究了时间一致的再保险-投资策略选择问题.在考虑再保险时,再保险保费按照方差值原理来计算;考虑投资时,风险资产服从带跳的随机微分过程.研究的目标是,求得时间一致的再保险-投资策略,以及相应的值函数.为了求解该问题,我们给出了一个检验定理;通过求解相应的HJB方程,求得了时间一致的再保险-投资策略,以及相应的值函数显式解.最后,分析了结果的经济意义,并通过数值算例解释了一些模型参数对最优策略的影响.

在将来,还有很多问题值得研究.比如:1) 本文的终止时刻T是确定,如果T是不确定,结果会怎样呢？2) 本文考虑的风险资产服从带跳的随机微分方程,如果风险资产满足其它模型,比如CEV模型、Heston模型等,结果会怎样呢？3) 本文在进行再保险时,假设再保险比例a(t)≥0;如果限制a(t)∈[0,1],即只考虑再保险不考虑购买新业务,则在求得再保险策略时,还要讨论a(t)的范围,因此处理起来会更麻烦.将来,我们会继续研究这些问题.