求二次比式和问题全局解的一个新的确定性算法

张博,高岳林

(1.北方民族大学数学与信息科学学院,宁夏 银川750021;2.宁夏科学计算与智能信息处理协同创新中心,宁夏 银川750021)

1.引言

分式规划问题是非线性全局优化的一个重要分支,而二次比式和规划问题是又一类特殊的分式规划问题.在现实生活中,许多实际问题均可抽象为二次比式和规划模型,且在投资问题、运输方案、经济效益、生产管理等领域有着广泛的应用背景.数十年来它吸引了许多专家和学者的高度关注;其次,从研究的观点来看,二次比式和规划问题对理论分析和计算求解的方式提出了挑战.本文主要考虑以下形式的二次比式和规划问题(QFP):

这里,p≥2,H1i(x),H2i(x)均为二次函数其表达式如下：

其中,b∈Rn,A∈Rm×n,Qsi∈Rn×n,qsi∈Rn,psi∈R,s=1,2,X是非空有界闭集.根据H2i(x)的连续性以及介值定理可知,对任意的x∈X有H2i(x)>0或者H2i(x)<0.如果存在某一个i∈{1,2,···,p}使得H2i(x)<0,用替代使得所有分式项的分母项均大于零;为了方便起见,假设此时,H1i(x)<0,H2i(x)>0,用替代其中M是一个充分大的正数,满足对所有的x∈X,H1i(x)+MH2i(x)≥0,问题(QFP)的本质不变.因此,这里不失一般性,假定对所有的i=1,2,···,p,均有H1i(x)≥0,H2i(x)>0.

此外,对于问题(QFP)可能拥有多个局部最优解,这样会干扰寻找全局最优解,使问题的难度增加,因此研究此类问题是必要的.本文为上述比式和规划问题建立了一个分支定界算法.首先,通过线性代数矩阵满秩分解的知识将原问题中通项的分子和分母的二次函数分别转化为相应的两项乘积和的形式,然后利用求解两项线性乘积和规划的知识[1]并结合一些线性化技巧分别构造问题目标函数中通项的下界,并基于此技巧构造出能够为原问题提供可靠下界的线性松弛规划问题.最后,利用分支定界的思想以及文[2]的可行域缩减技术设计出关于本文问题的一个新的分支定界算法.

到目前为止,已经有许多全局优化算法可以用来求解比式和规划问题.当通项中的分子和分母都为线性函数时,那么文[3-9]给出了不同的求解方法,当问题为非线性比式和规划问题时,ZHANG,CHEN和JIA[10]提出了一种基于单调优化理论的算法用于求解此类问题.JIAO和LIU[11]构造了一种区间划分压缩算法并用求解二次比式和规划问题.最近,JIAO和LIU[13]他们又提出了一种基于参数线性松弛规划问题来确定下界的方法,并构造了相应的分支定界算法来求解二次比式和规划问题.文[14]为广义多项式比式和问题,GAO,Mishra和SHI讨论了函数比之和的最大化问题,推广了一种求解线性比和问题的算法,并给出了问题的复杂性.文[15]给出了一种基于单纯形剖分的确定性非线性比式和问题全局优化算法.关于其他类型非线性比式和规划问题还可以参考文[16-17].

本文后续章节布局如下:第二节给出问题预处理时必要的两个引理;第三节利用已知的两个引理得出原问题的一个等价问题并给出等价问题的线性松弛过程;第四节给出了新的分支定界算法以及相应的超矩形剖分方法和缩减技术,并证明了算法的收敛性;第五节通过数值实验说明了我们提出的算法是有效可行的;第六节为结论.

2.预备知识

为了求解问题(QFP),我们首先将其转化为一个具有特殊结构的等价问题以便建立线性松弛问题,为了验证这种转化的可能性,我们首先引入以下引理:

引理2.1[12]对任意矩阵Q满足秩(Q)=1,存在两个向量α和β,使得Q=αβT.

引理2.2[12]对任意矩阵Qsi∈Rn×n,假定秩(Qsi)=rsi,则一定存在两个向量αsij和βsij,使得

3.等价问题以及线性松弛规划

根据以上两个引理2.1 和2.2 我们知道,对每一个i=1,2,···,m,s=1,2,二次函数Hsi(x)都可转化为以下形式:

那么问题(QFP)可以进一步转化为以下等价问题:

其中,αsij∈Rn,βsij∈Rn,qsi∈Rn,psi∈R,i=1,2,···,p,s=1,2,X是非空有界闭集.

为了获得问题(QFP)的分支定界算法,我们需要确立线性松弛规划子问题,用于估计问题(QFP)最优值的下界,具体方法如下:

首先,求解以下2n个线性规划问题:

从而得到包含可行域X的初始超矩形

然后,对每一个i=1,2,···,p,s=1,2,j=1,2,···,rsi,继续求解以下线性规划问题:

根据式(3.2)和(3.3)很容易得到

再由(3.4)-(3.7),不难得出

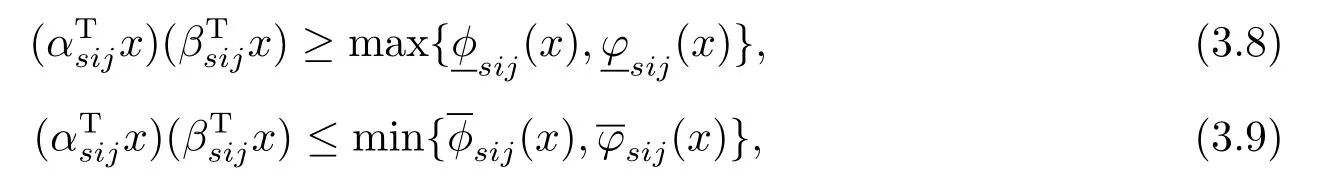
这里,

为了方便起见,这里记

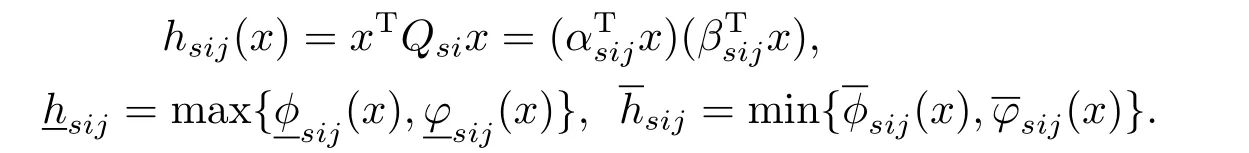
定理3.1令则对所有的x∈X ∩H,当εk→0时,hsij(x)−

证对所有的x∈X ∩H,由式(3.8)得:

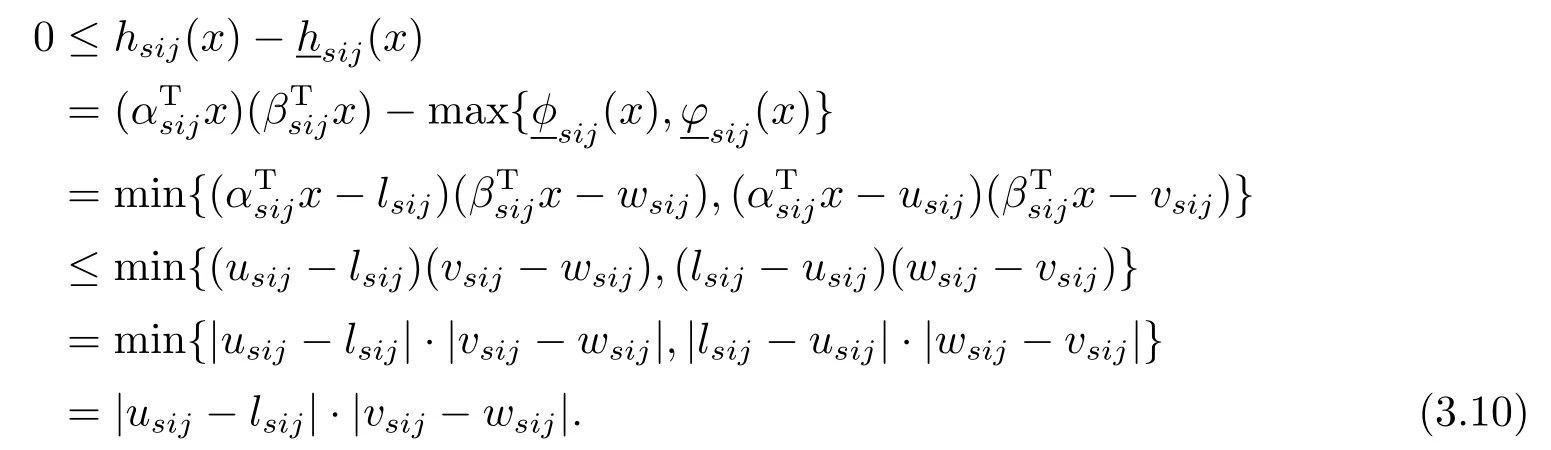
同样有(x)−hsij(x)→0.证毕.

不失一般性,对任意的x∈Hk ⊆H,i=1,2,···,m,定义

定理3.2对任意的以下结论成立:

证(i)对任意的x∈Hk,以及i=1,2,···,p,根据(3.10)可知,当s=1 时,

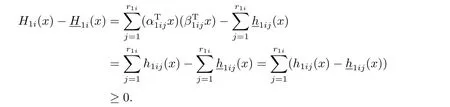
同理,根据式(3.11)可知,当s=2时,因为H2i(x)>0,所以(x)≥H2i(x)>0.虽然H1i(x)≥0,但是存在x∈Hk使得(x)<0,以及G(x)<0,此种情况下,显然G(x)>G(x),满足结论(i);当H1i(x)≥0即0 时,同样满足结论(i).

基于上述讨论,可以知道,对每一个i=1,2,···,p,H1i(x),H2i(x),(x)都是大于零的并且都是连续的,所以它们在有界闭集X,H以及剖分后的子区域Xk,Hk上都是有界并且是非负的,那么分别存在相当大的正数N1i,N2i使得记根据式(3.12)可知

那么,根据上述讨论,我们就得到了问题(QFP)的非线性松弛规划子问题(NLRP(Hk)):

显然,(NLRP(Hk))可以转化为(QFP)的一个线性松弛规划子问题(LRP(Hk)):

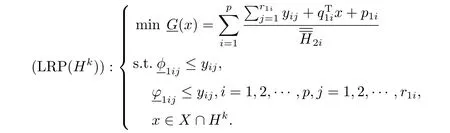
综上所述,我们知道在算法迭代到第k步时,只要在此步所对应的超矩形Hk上求解问题(LRP(Hk)) 的最优值v(LRPk),那么这个最优值同时也是原问题(QFP) 在Hk上全局最优值v(QFP)的一个下界,即v(LRPk)≤v(QFP).

定上界的操作是在分支的过程中不断产生问题(QFP)的可行点来完成的.通过求解原问题在Hk上的一个有效下界v(LRPk),它的最优解是原问题在Hk上的一个可行点,而我们通过在分支定界的过程中不断增加满足可行域X的可行点,以达到更新上界的目的.

4.超矩阵的剖分和缩减

在这一节,我们给出超矩形的分支、缩减步骤对应的算法(RPF)和算法(RSA).

首先,为了便于本文算法的分支,这里采用二分法的思想.令Hk=[lk,uk]∈H表示当前所要剖分的超矩形,用xk表示问题(QFP)当前最优解,显然xk∈X ∩Hk.假设xk∈Hk,对超矩形Hk=[lk,uk],我们给出算法(RPF)用来对其剖分:

算法(RPF):

步1计算ω=max{(xkj−lkj)(ukj−xkj):j=1,2,···,n},

若ω=0,

令ukµ−lkµ=max{ukj−lkj:j=1,2,···,n},

否则,找出第一个xkj∈arg maxω,记作xkµ=xkj.

记x′=(lk1,lk2,···,lkj−1,xkµ,lkj+1,···,lkn)T,x′′=(uk1,uk2,···,ukj−1,xkµ,ukj+1,···,ukn)T.

步2通过x′与x′′的连线或它们连线所在的平面将超矩形Hk剖分为两个子超矩形Hk1=[lk1,uk1]和Hk2=[lk2,uk2],则这两个子超矩形分别为:

其次,为了提高算法的收敛速度,这里使用文[10]中的超矩形缩减技术.假设问题(QFP)中的所有线性不等式约束的展开形式为:∑aijxj≤bi,i=1,2,···,m,文[10]中的超矩形缩减技术可以表述为算法(RSA):

算法(RSA):

令Ik:={1,2,···,m},

步1对每一个i=1,2,···,m,

分别计算rUi=

步2若rLi >bi,停止.问题(QFP)在Hk上没有可行解(Hk被删除);

若rUi≤bi,令Ik:=Ik−{i},问题(QFP)的第i个线性不等式约束被删除;

否则,对每一个j=1,2,···,n

若aij >0,令

否则aij <0,令

为了方便起见,我们把该算法产生的新的超矩形仍然记为Hk,它是原来超矩形的子集.

5.新的分支定界算法及其收敛性

最后,基于上述讨论,本文求解问题(QFP)全局最优解的分支定界算法总结如下:

步0(初始化)

步0.1构造包含可行域X的n维超矩形H0=H=[l,u];令分支的所有活跃节点的集合记为Q0={H0},上界为U0=+∞,将本文上述所有可行点都放入集合W中,所需容忍度ϵ>0.

步0.2解线性规划问题(LRP(H0)),如果不可行,那么原问题无解;否则,记得到的最优值和最优解分别为L(H0),(x0,y0),置L0=L(H0);如果x0∈X,令W=W ∪{x0},U0=G(x0),若U0−L0≤ϵ,那么称x0为问题(QFP)的ϵ-全局最优解,迭代终止;否则,置k=1,转入步1.

步1(超矩形的分支和缩减)

在Qk中挑选出当前最小下界所对应的超矩形Hk,超矩形Hk直接经过剖分算法(RPF)的分解可产生形如第四节中的两个新的子超矩形Hk1和Hk2;然后运用算法(RSA)分别对Hk1和Hk2按以下步骤缩减,为了方便起见,我们把缩减后的超矩形记为Hki,i∈Γ,其中Γ是缩减后超矩形的指标集合.

步1.1运用算法(RSA)对Hk1进行缩减.

若Hk1被删除,则Qk=Qk{Hk},转到步1.2;

否则,令Qk=Qk{Hk}∪Hk1;

求解线性松弛规划问题(LRP(Hk1)),得到最优值记为Lk1,最优解记为(xk1,yk1);

若xk1∈X,让W=W ∪xk1,转到步1.2;

步1.2运用算法(RSA)对Hk2进行缩减,

若Hk2被删除,

若Hk1已经被删除,转到步3;

若Hk1没有被删除,转到步2;

否则令Qk=Qk ∪Hk2;

求解线性松弛规划问题(LRP(Hk2)),得到最优值记为Lk2,最优解记为(xk2,yk2);

若xk2∈X,让W=W ∪xk2,转到步2;

步2(定界)

如果W=∅,那么Uk=+∞;如果W≠∅,那么Uk=min{G(x):x∈W},当前的最优解为xk∈arg minG;

如果Qk=∅,那么Lk保持不变;如果Qk≠∅,那么Lk=min{L(H):H∈Qk};

步3(剪枝规则)

让Qk+1=Qk{H:Uk−L(H)>ε,H∈Qk}.若Qk=∅,迭代终止:Uk是(QFP)的ϵ-全局最优值,xk是ϵ-全局最优解,否则,置k=k+1,转到步1.

下面为了说明我们算法是收敛的,给出定理5.1并给予相应的证明.

定理5.1设问题(QFP)的可行域X是n维的,且超矩形的剖分是耗尽的,那么以下两个结论成立:

(i)如果算法在迭代过程中有限步终止,则问题(QFP)的全局最优解将在算法终止时得到;

(ii) 如果算法在有限步不能终止,则将产生可行解组成的序列{xk}并且它的每一个聚点x∗必是问题(QFP)的全局最优解.

证(i)若算法是有限步终止,那么根据终止准则可知Uk−Lk <ϵ.步2和步3暗示了

假设此时的全局最优解是x∗,我们知道

因此,将式(5.1)和(5.2)联立可得

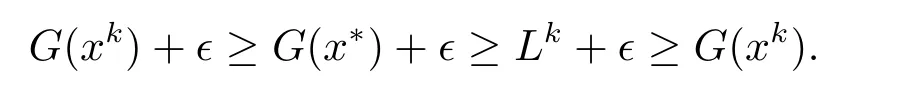
故(i)得证.

(ii)如果算法的迭代是无限的,则通过求解问题(LRPk)可产生原问题的可行解序列{xk},以及对应的序列{(xk,yk)}.根据步1,随着可行域的不断加细我们有

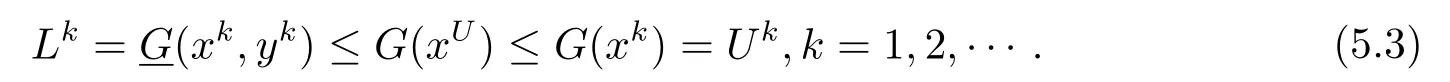
因为下界序列{Lk=(xk,yk)}是单调不减且有界的,且上界序列{Uk=G(xk)}是单调不增且有界,故原问题的上下界都是收敛的.对式(5.3) 两边取极限可得

于是,令L=那么式(5.4)将转化为

不失一般性,假设算法在迭代过程中形成的超矩形序列{Hk=[lk,uk]}满足xk∈Hk以及Hk+1∈Hk.由于算法在每步迭代中剖分超矩形都是沿着最长边来剖分的,这保证了超矩形尽最大可能的加细,那么在这个过程中也会形成关于x的序列{xk}同时满足根据函数G(x)的连续性,就会有

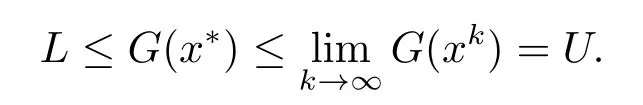
所以,序列{xk}的每一个聚点x∗都是问题(QFP)的全局最优解.

6.数值实验

在这一节,我们用几个其他文献中已知的算例来测试文中算法的有效性.本文所有的线性规划问题均选用单纯形法求解,算法所有测试过程均用MATLAB9.0.0.341360(R2016a) 在Inter(R)Core (TM)i5-3570K,CPU@3.2GHz,4GB 内存,64 位Windows7 操作系统的计算机上运行.

算例1[11,14,16]:

算例2[11,13]:

算例3[13,14,16]:

算例4[14,16]:

算例5[11,17]:

算例1-5的计算结果我们已呈现在表6.1中,算法运行过程中的容忍度分别为10−3,10−5,10−2,10−2,10−6,显然从表6.1中我们知道这些容忍度分别为其他各个文献中所用容忍度的最大值,足以与其他算法对比.通过表6.1可以看出,本文算法总体来说比文[11,13,17]计算效果要好,与文[14]相比,我们算法仅在算例3表现的更好,其他算例表现略差,虽然总体计算能力低于文[16]中的算法,但是我们所提出的算法是有效可行的.

为了进一步说明本文算法的性能,对于算例6,我们也进行了若干的伪随机试验并呈现在了表6.2中,下文也做出了对应的说明.

表6.1 算例1-5 利用本文算法产生的数值结果

表6.2 算例6 利用本文算法产生的数值结果

算例6:

这里,A,b,αsij,βsij,qsi,psi,s=1,2,i=1,2,···,p,j=1,2,···,r,的每个元素都是在[0,1]上伪随机产生的,r表示矩阵的秩.

表6.1和表6.2中,表头的符号分别是:E:算例编号;R:计算方法;x∗:原问题的最优解;G(x∗):目标函数的最优值;I:平均迭代次数;ϵ:容忍度;t:迭代终止时CPU平均运行时间;p:目标函数中二次比式的个数;r:目标函数分子和分母中矩阵的秩,这里假设它们秩都相等;m:线性约束的个数;n:目标函数的维数.

通过表6.2的计算结果,可以知道当m,r和n固定不变时,随着p的增加,算法的平均迭代次数I在缓慢增加,但是迭代时间t增加的很快;当p,r和n固定不变时,约束条件增多时,I和t都是快速减少的;当p和m保持不变时,随着维数n的增加,I和t都是急剧增加的,此时若将矩阵的秩变小,那么相应的I和t也在减少;当约束条件的个数m相对于决策变量个数n非常大时,因为这样形成的可行域非常狭小,所以能够在很少的迭代步骤找到最优解,但是每一步的迭代时间都很长;当决策变量个数n相对于约束条件的个数m很大时,形成的可行域范围很大,迭代时间和步骤都变大.