基于Delaunay三角剖分处理二维欧式空间MTSP的近似算法

寿 涛, 刘朝晖

(华东理工大学数学系,上海 200237)

基于Delaunay三角剖分处理二维欧式空间MTSP的近似算法

寿 涛, 刘朝晖

(华东理工大学数学系,上海 200237)

考虑了在二维欧式平面内的多旅行商问题,通过Delaunay三角剖分的方法,将问题转化为求解多个旅行商问题。树分解算法的核心是Delaunay边的空圆性质并且可以证明该算法的近似比为2。最后,通过数值模拟验证了算法的有效性。

MTSP; Delaunay三角剖分; 近似算法

多旅行商问题(MTSP)是TSP问题的推广[1]。通常可以把MTSP问题拆分成2个子问题,即:先确定每个旅行商访问客户点集;再对每个旅行商访问的点求解TSP问题。对于MTSP问题的研究,最早可以追溯到1990年Li等[2]的5近似算法。之后Harks等[3]给出了该问题的4近似比算法。Rathinam等[4]在2006年给出了基于欧式距离下MDVRP问题的2近似算法。Malik[5]则在2007年给出了推广的多旅行商问题的2近似算法。上述文献中的算法大多基于双生成树算法[6]。此外,邻域搜索算法也是处理MTSP的经典方法,如Aarts等[7]讨论了组合优化中邻域算法的重要性以及Angel[8]对于邻域算法在各种条件下的最坏情况研究。直到2011年Zhou等[9]给出了理论近似比为(2-1/k)的算法,其中k为旅行商个数,该算法主要基于Christofides算法[10]。

本文将讨论在二维平面内MTSP问题:对于平面中点集V={v1,v2,…,vn},D为旅行商集,使得每个V中的每个点当且仅当被一个旅行商访问,并最小化访问总路程。随后引入Delaunay三角剖分概念,进而优化最优路线。

1 Delaunay三角剖分

网格剖分是平面可视化的关键技术,早期的网格剖分主要基于矩形和正六边形,后来为了增加灵活性发展为三角形[11]。在20世纪80年代末,三角形的网格剖分技术已经在船体建模、桥梁受力等实际问题中有着广泛的应用。本文给出三角剖分的概念,且介绍Delaunay三角剖分。

定义1若由平面上的点集V与其构成的边集E组成的平面图G(V,E),满足下列条件,则称其为三角剖分:(1) 平面中不含孤立点;(2) 每个面均为三角形,且三角面的合集为该点集的凸包。

若在生成三角剖分的过程中提出若干个优化条件,如最小化边的总长度、最大化边的总长度、最大化最小角等,将会得到不同意义下的三角剖分。Delaunay三角剖分是满足最小角达到最大条件的三角剖分。在二维空间中,对于每个三角剖分总存在一个最小角,值得注意的是这种思想仅在二维空间中成立,因为在三维及更多维空间中,单纯体的内角和并不是一个常值[12]。因为这个特性,Delaunay三角剖分总是尽可能避免生成“瘦长”的三角形,进而尽量生成“等边”的三角形[13]。通常生成Delaunay三角剖分的过程,就是实现三角剖分中所有三角形的外接圆内不含其他点的过程[14]。

定义2给定点集V={v1,v2,…,vn,},将连接其中两点v1,vj的边e称为Delaunay边,当且仅当存在一个经过v1,vj两点的圆,且圆内不包含V中的其他点。同时若V的一个三角剖分中只包含Delaunay边,则称这个三角剖分为Delaunay三角剖分。

对于给定的点集,通常情况下其Delaunay三角剖分是唯一的,但是当存在四点或多于四点共圆的情形,则该点集的Delaunay三角剖分不唯一。生成Delaunay三角剖分,若从贪心算法出发,则至少要在O(n2)时间内才能完成[13]。如果从最近点意义下的Voronoi图出发,则可以通过Fortune算法构造Delaunay三角剖分,且时间复杂度为O(nlogn)。定义2可以通过局部变换法的思想实现,该算法通过将边翻转的方式来寻找Delaunay边,直到所有的边都满足定义2从而算法终止[15]。事实上,寻找Delaunay边的过程就是最大化最小角的过程,因为在将边翻转的过程中,总是优先生成“等边”的三角形,同时避免生成“瘦长”的三角形。

定义3在V的Delaunay三角剖分的边集中,包含一棵V的欧几里得最小支撑树,即EMST。

证明 运用反证法,假设T为点集V上的一棵欧几里得最小支撑树且在T的边集中除了边e其他边均为Delaunay三角剖分中的边,那么记T1,T2为边e连接的2个子树,且v1,v2为边e相关联的点。根据定义2,则可以得到对于经过任意v1,v2两点的圆内都包含其他点,考虑以边e为直径的圆的情况,其中存在一个其他的点a,假设点a为T1上的点。此时将a与v2连接,那么会得到一条比e更短的边,与假设矛盾,故得证。

2 算法

2.1 树分解算法

对于给定的点集V,其中点的个数为n,若直接生成EMST,则算法的复杂度为O(n2logn),但是当引入Delaunay三角剖分的方法,则可以将复杂度降低到O(nlogn)。树分解算法的详细步骤如下:

(1) 基于所给的点集V,产生Delaunay三角剖分;

(2) 对于Delaunay三角剖分,生成最小支撑树;

(3) 对最小支撑树中的边ei,进行降序排列,即为S;

(4) 从S中依次对最小支撑树进行删边处理:若删去ei,能保证每个连通分支至少有一个旅行商,则删去,否则保留;

(5) 重复第4步,直到生成的k个连通分支,其中k为旅行商个数;

(6) 运用双生成树算法,产生k条汉密尔顿回路。

2.2 算法近似比

首先介绍一些算法中的记号,把W记作树分解算法得到的解,d(W)记作W的解值,此外,Wi代表的是由第i个旅行商在近似算法中访问的客户点集,TWi表示在近似解中的第i棵子树。作为对应,在最优解中,OPT记为最优解,d(OPT)记为最优解值,Hi代表的是由第i个旅行商在最优中访问的客户点集,THi表示在最优解中的第i棵子树。

定义4树分解算法的近似比为2。

证明 情况1:Wi与Hi相同,其中i为1～k中的任意值。

在这种情况下必定会有d(TW)=d(TH),可用反证法证明,将边重复并删去重复点生成回路,可得到d(W)≤2d(OPT),故得证该算法的近似比为2。

情况2:在近似解和最优解的子树中,除了i=k,k′这两棵子树不同外,其他子树均相同,具体细节如图1所示。

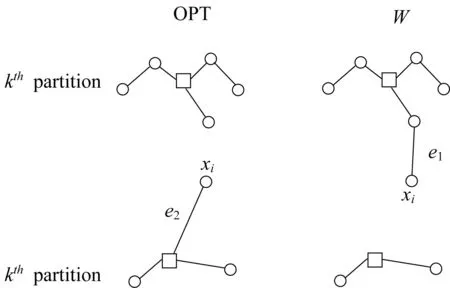
图1 情况2中的最优解与近似解的子树Fig.1 Subtree of OPT and W in case 2

在上述情形中,假定Hk包含n1个点,而Hk′包含n2个点,在Wk中包含(n1+1)个点,在Wk′包含(n2-1)个点。对于点xi,根据树分解算法,若可去边为e2而不是e1时,则必有e1≤e2,所以必有d(TWk)+d(TWk′)≤d(THk)+d(THk′),从而得证。

情况3:情况3为情况2的补充,具体细节如图2所示。

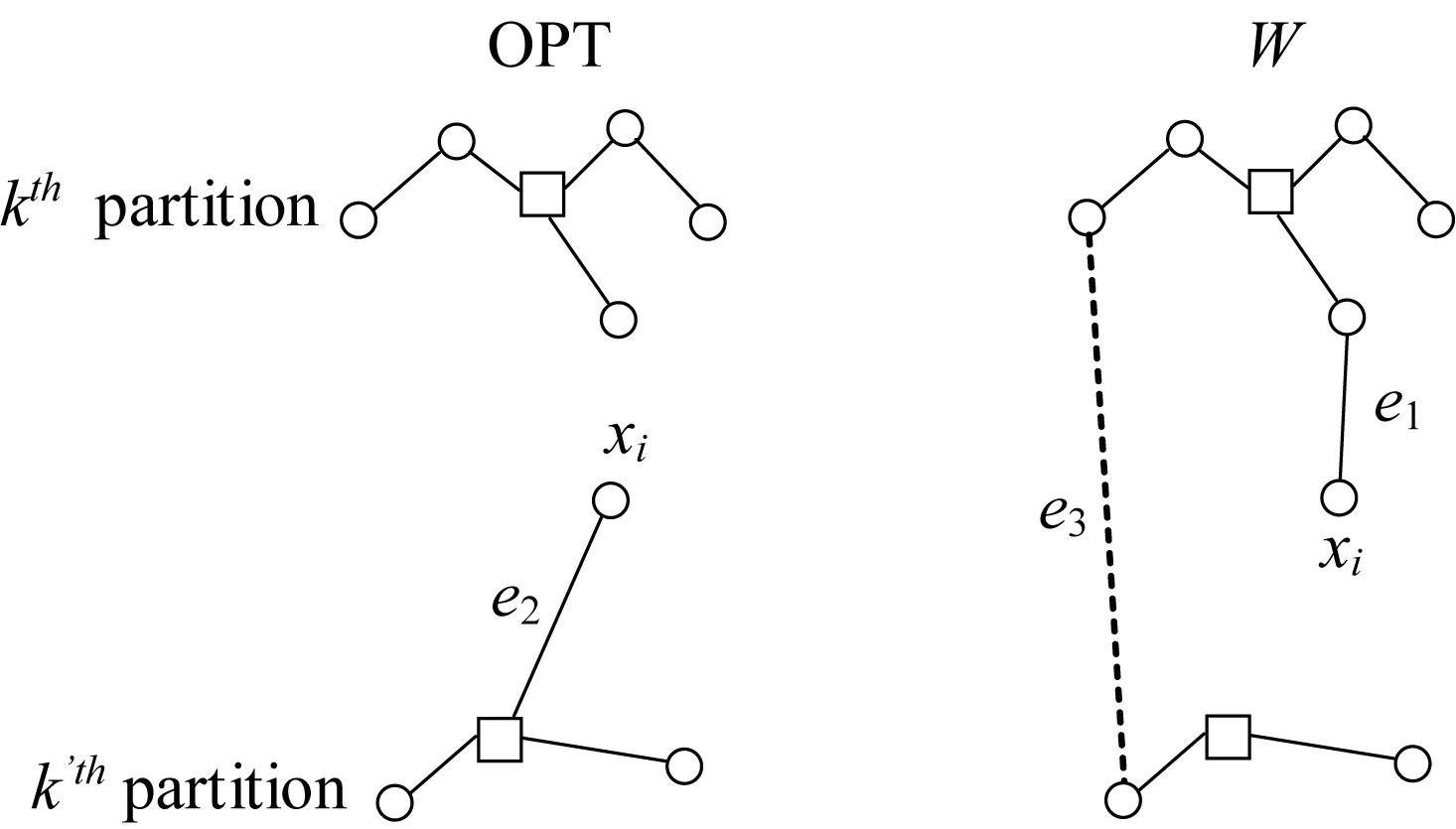
图2 情况3中的最优解与近似解的子树Fig.2 Subtree of OPT and W in case 3

由于边e3不与点xi相关联,可得到d(TWk)+d(TWk′)≤d(THk)+d(THk′)。因为根据算法,若有e3>e2,则最小支撑树中一定会包含e2。此外由于e1

3 数值模拟

将从TSPLIB数据库上选取一些例子用于数值模拟,并将结果与Rahinam的2近似算法进行对比。

从TSPLIB数据库中挑选9个实例(Ei151,Ei176,Rat99,Ch130,Rat195,Tsp225,A280,Lin318,Rd400)并随机设定旅行商点来对比算法的表现。将Rathinam的2近似算法作为参照[16],下面以ei151为例进行演示。

首先,随机挑选第3,7,11,25,34,41这6个点作为旅行商。运行树分解算法,将得到6个环游,依次如下:第1个为14,25,14;第2个为3,20,35,36,3;第3个为11,32,1,22,11;第4个为43,7,23,24,43;第5个为13,41,19,40,42,13;第6个为2,29,21,50,34,30,9,38,5,49,10,16,39,33,45,15,44,37,17,4,18,47,12,46,51,27,48,6,8,26,31,28,2。运行Rathinam的算法可得6个环游:第1个为14,25,14;第2个为43,7,23,24,43;第3个为5,38,11,32,1,22,5;第4个为43,7,23,24,43;第5个为13,41,19,42,40,13;第6个为2,29,21,50,34,30,9,49,10,16,39,33,45,15,44,37,17,4,18,47,12,46,51,27,48,6,8,26,31,28,2。具体细节如表1所示。

表1 不同实例下解值的对比

4 结束语

Delaunay三角剖分是计算几何中常用的方法,但是在MTSP问题的研究中,却很少涉及。本文将MTSP问题限定在二维平面中,并将Delaunay三角剖分应用于此,同时引入树分解算法。该算法的理论性能比与时间复杂度比较稳定,并且在实际的数值模拟中,能处理一些中型的实例问题,且能给出较优的解。

[1] GAREY M R,JOHNSON D S.Computers and Intractability:A Guide to the Theory of NP-Completeness[M].New York:W.H.Freeman,1979:206-218.

[2] LI C L,SIMCHI-LEVI D.Worst-case analysis of heuristics for multidepot capacitated vehicle routing problems[J].Informs Journal on Computing,1990,2(1):64-73.

[3] HARKS T,KONIG F G,MATUSCHKE J.Approximation algorithms for capacitated location routing[J].Transportation Science,2013,47(1):3-22.

[4] RATHINAM S,SENGUPTA R,DARBHA S.A resource allocation algorithm for multivehicle systems with nonholonomic constraints[J].IEEE Transaction on Automation Science,2007,4(1):98-104.

[5] MALIK W,RATHINAM S,DARBHA S.An approximation algorithm for a symmetric generalized multiple depot,multiple travelling salesman problem[J].Operations Research Letters,2007,35(6):747-753.

[6] ROSENKRANTZ D J.An analysis of several heuristics for the traveling salesman problem[J].SIAM Journal of Computing,1977,6(3):563-581.

[7] AARTS E,LEBSTRA J.Local search in combinatorial optimization[D].USA:Princeton University Press,2003.

[8] ANGEL E.A survey of approximation results for local search algorithms[M].Heidelberg:Springer,1970:30-73.

[9] XU Z,XU L,RODRIGUES B.An analysis of the extended Christofides heuristic for the k-depot TSP[J].Operations Research Letters,2011,39(3):218-223.

[10] CHRISTOFIDES N.Worst-Case Analysis of a New Heuristic for the Travelling Salesman Problem[D].USA:Carnegie Mellon University,1976.

[11] 徐永安,杨钦,吴壮志,等.三维约束Delaunay三角化的实现[J].软件学报,2001,12(1):103-110.

[12] JOE B.Delaunay versus max-min solid angle triangulations for three dimensional mesh generation[J].International Journal of Numerical Methods in Engineering,1991,31(5):987-997.

[13] DE BERG M,VAN KREVELD M,OVERMARS M.Computational geometry:Algorithms and applications[J].Computational Geometry Algorithms & Applications,2013,19(3):333-334.

[14] LEE D T,SCHACHTER B J.Two algorithm for constructing a Delaunay triangulation[J].International Journal of Parallel Programming,1980,9(3):219-242.

[15] MARCUM D L,WEATHERILL N P.Unstructured grid generation using iterative point insertion and local reconnection[J].AIAA Journal,1995,33(9):1619-1625.

[16] RATHINAM S,SENGUPTA R,DARBHA S.A resource allocation algori-thm for multivehicle systems with nonholonomic constraints[J].IEEE Transactions on Automation Science and Engineering,2007,4 (1):98-104.

ApproximateAlgorithmofMTSPon2DEuclideanSpacewithDelaunayTriangulation

SHOUTao,LIUZhao-hui

(DepartmentofMathematics,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

This paper discussed Multi Travelling Salesman Problem (MTSP) on 2D Euclidean space.This problem could be simplified to solve several TSP by Delaunay Triangulation.It could be proven that the approximate ratio of Tree Decomposed Algorithm was 2 and the core proof was based on empty circle property of Delaunay edge.The paper testified the performance and efficiency of the algorithm by some numerical examples.

MTSP; Delaunay triangulation; approximate algorithm

1006-3080(2017)06-0895-04

10.14135/j.cnki.1006-3080.2017.06.022

2017-01-16

寿 涛(1991-),男,上海人,硕士生,研究方向为优化理论与应用。E-mail:603077928@qq.com

刘朝晖,E-mail:zhliu@ecust.edu.cn

O224

A