滑动法关间隙过程中横腭杆对上牙弓宽度的影响：三维有限元研究

李毕超 高瑜 武姗 项桦 任利玲

临床上，横腭杆（the transpalatal arch，TPA）主动加力不仅可以扭正、直立磨牙，还能扩弓纠正磨牙宽度不调；其被动就位后能发挥支抗作用，可阻碍支抗牙的旋转和横向移动［1-4］。目前，多数文献主要研究TPA对支抗牙三维方向的影响，而在拔牙病例间隙关闭过程中其对牙弓中后段牙齿横向移动有何影响尚无文献报道。因此，本实验通过建立滑动法关间隙的三维有限元模型，探讨间隙关闭过程中TPA（Goshgarian型）对尖牙、第二前磨牙、第一磨牙和第二磨牙横向移动的影响及其在间隙关闭量为0、2、4 mm时不同阶段对各牙横向移动的影响趋势。

1 材料与方法

1.1 建立滑动法关闭拔牙间隙的上颌模型

1.1.1 上颌牙颌系统三维模型的建立 选择拔除上颌双侧第一前磨牙、经排齐整平准备内收的成人男性患者1名，双侧拔牙间隙平均剩余6.05 mm。将其以DICOM格式储存的上颌牙颌系统的CBCT（Planmeca公司，ProMax®，芬兰）影像数据导入Mimics 19.0软件（Materialise公司，比利时）。通过阈值划分建立上颌骨、上牙列的Mask层，并以Calculate 3D指令生成相应的上颌骨、上牙列初始三维模型。利用逆向工程软件Geomagic studio 2015（3D Systems公司，美国）对上颌骨、上牙列模型表面进行修复、优化，通过Offset指令将优化后的上颌牙根外表面向外扩展0.2 mm［5-6］，根据布尔逻辑运算得到各牙的初始牙周膜模型；同时将上颌骨向内偏置1.5 mm以形成骨皮质与骨松质结构，使用曲面功能建立牙周膜、骨皮质、骨松质、上颌牙列的实体模型，并通过前牙整体向后移动建立内收量为2、4 mm模型（原始模型内收量为0 mm），使用雕刻功能调整牙列移动后的牙槽骨厚度。

1.1.2 弓丝、托槽、及横腭杆等模型的建立 在Unigraphics NX 8.5软件（Siemens公司，德国）中，按照美国3M公司生产的MBT托槽数据［7-8］建立0.56 mm×0.70 mm槽沟系统的托槽。根据现有的牙弓形态建立弓丝尺寸为0.48 mm×0.64 mm的主弓丝模型，通过曲线建模，利用扫掠功能建成直径为0.9 mm的横腭杆，测绘牵引钩实物尺寸利用NX 8.5软件的草图建模建立牵引钩模型。

1.1.3 滑动法关闭拔牙间隙有限元模型的建立 根据内收量为0、2、4 mm不同阶段及使用TPA与否将上述模型组装成6个模型（0 mm指拔牙间隙尚未开始关闭，2、4 mm指拔牙间隙已减小2、4 mm），导入Ansys workbench 15有限元分析软件（ANSYS公司，美国）进行网格划分、属性定义以及边界的设定，建立最终的三维有限元模型。

1.2 实验设定

设定各种组织为各向同性、连续均质的线弹性体，受力变形为小变形，材料的弹性模量与泊松比参数见表1。模型采用四面体十节点单元，将托槽与牙齿及其与弓丝间接触方式分别设定为Bonded和Frictional类型，摩擦系数为0.2［9］，即托槽与牙齿间为固定接触，但与弓丝间可发生相对滑动。设定尖牙牙尖、第二前磨牙颊尖及根尖点、第一、二磨牙近中颊尖、近中颊根及腭根根尖点为参考点，由于模型左右基本对称，计算时仅统计右侧各牙及参考点的位移。关于坐标系统，设定各牙近远中向、颊（唇）舌向、龈向分别为X、Y、Z轴，近中、舌向、龈向为正（图1）。在Ansys workbench 15模拟的6个工况中，设定滑动牵引钩与颊钩间加载力为1 N［2］。

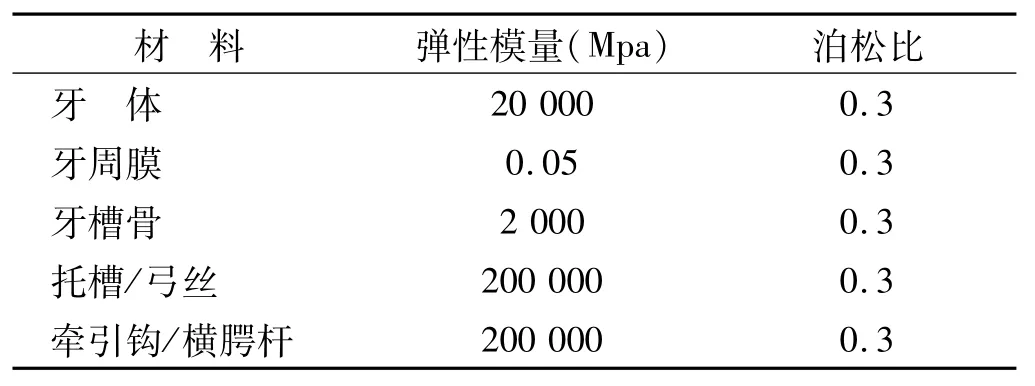
表1 相关材料力学性能参数Tab 1 Material properties of FEA model

图1 各牙的三维坐标系Fig 1 The coordinated system of model

2 结 果

2.1 尖牙移动趋势

6种工况下，尖牙均表现为牙冠舌向移动，牙根唇向移动，牙冠移动量大于牙根，各牙冠根位移量见表2，在间隙关闭量为0、2、4 mm阶段，无论TPA组还是对照组（Non-TPA组）尖牙牙根唇向位移仅少量减小，而牙冠舌向位移则明显减小，4 mm组牙冠舌侧位移约为0 mm组的1/3，表明间隙关闭后期尖牙牙冠舌向移动逐渐变小。TPA组与对照组在以上3个阶段中的尖牙牙冠舌侧位移量分别为：0.145、0.115、0.034 6 mm和0.151、0.122、0.053 mm（表2），TPA组在间隙关闭各阶段牙冠舌侧位移量均小于对照组，表明TPA一定程度上维持了牙弓的宽度；此外，通过TPA组与对照组位移量的差值除以对照组位移量作为评价在间隙关闭各阶段TPA的横向效应，结果表明，较之Non-TPA组，在间隙关闭量为0、2、4 mm时，尖牙舌向位移分别减少了3.8%、6%、34.7%，平均为14.8%，表明在间隙关闭后期TPA对尖牙的横向效应明显增加（图2～4）。

2.2 第二前磨牙移动趋势

6种工况下，第二前磨牙牙冠、牙根均表现为舌向移动，牙冠移动量大于牙根；2、4 mm组牙冠舌侧位移量相似略大于0 mm组；TPA组与Non-TPA组相比舌向移动分别减少了33%、31.2%、24.9%，平均减少了29.7%（图2）。

表2 不同加载情况下各牙的横向位移变化 （mm）Tab 2 Displacement of posterior teeth under different loading conditions in transverse direction （mm）

图2 不同加载情况下牙冠的横向位移趋势Fig 2 The tendency of transverse displacement under different loading conditions

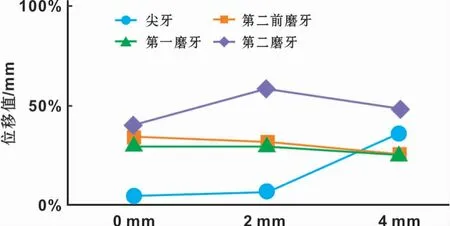
图3 不同加载情况下上颌后牙TPA效应量Fig 3 The efficiency of TPA about maxillary posterior teeth under different loading conditions

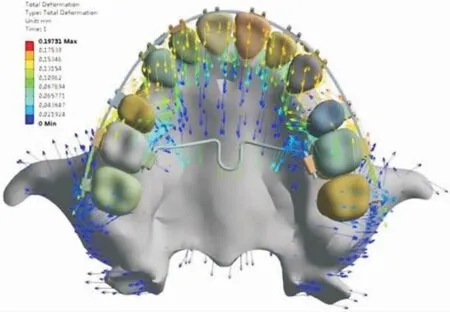
图4 TPA组（2 mm）加力后各牙移动趋势Fig 4 The movement tendency of teeth after loading in TPA group（2 mm）

2.3 第一磨牙移动趋势

6种工况下第一磨牙为冠舌向、根唇向移动，牙冠位移量略大于牙根；2、4 mm组牙冠位移量相似，略大于0 mm组；与Non-TPA组相比，TPA组第一磨牙牙冠舌侧位移量分别减少了29.7%、28.9%、24.4%，平均减少了27.7%，与第二前磨牙相似，在间隙关闭的各阶段，TPA对第一磨牙的横向效应有减小的趋势（图2）。

2.4 第二磨牙移动趋势

6种工况下第二磨牙均表现为牙冠颊向、牙根舌向移动，牙冠位移大于牙根；0 mm组牙冠颊向位移值最大，其次为4 mm组，2 mm组最小；与Non-TPA组相比，TPA组牙冠颊向移动分别增加了39.4%、57.7%、47.6%，平均增加了48.2%，而牙根舌向移动量均较小，表明间隙关闭过程中TPA的使用有加重第二磨牙颊向倾斜的趋势（图2）。

3 讨 论

除颅面部持续生长影响外，牙齿移动到新的位置后牙周组织的改建常需4～8个月的时间，因而正畸矫治后牙齿、牙弓形态较不稳定易复发到治疗前的状态，其中尖牙和磨牙尤为明显，矫治过程中尽量维持牙齿原始位置及牙弓原有形态有利于治疗后的稳定［10-12］。临床上，拔牙病例随着间隙的关闭，前磨牙和磨牙间宽度均有所减小［13］，而TPA被动置入可有效防止支抗牙扭转及横向移动［2］，本实验通过三维有限元方法进一步探讨TPA在滑动法关间隙过程中对牙弓中后段牙齿横向移动的影响。

该研究发现尖牙、第二前磨牙、第一磨牙牙冠在间隙关闭过程中均表现为舌向移动，TPA组较对照组移动量小；第二磨牙牙冠颊向移动，TPA组较对照组移动量大。多数临床研究［14-17］发现拔牙病例矫治后第二前磨牙、第一磨牙间宽度减小，与本实验结果一致，但尖牙间宽度增加、第二磨牙间宽度减小与本实验结果相反。上述研究比较了整个正畸治疗前、后同名牙间的宽度变化，而治疗的各阶段都可能存在牙齿三维方向的变化，本实验则仅研究间隙关闭过程中上牙弓宽度变化，且以上研究均未告知拔牙病例间隙关闭过程中是否使用TPA等，因而可能与本实验结果有一定的差异。三维有限元分析方法不能模拟牙槽骨的改建，所有牙齿的移动均为牙周膜受力形变产生的初始位移［9，18］，Kojima等［9］学者利用三维有限元迭代运算模拟牙槽骨的连续改建以分析滑动法关闭拔牙间隙过程中前牙的移动趋势，结果发现加力初期前牙表现为牙冠舌倾的倾斜移动，但经过多次迭代运算后则为整体移动，并认为不能通过初始移动类型来判断牙齿的远期移动方式。本实验建立了内收量为0、2、4 mm不同阶段的三维有限元模型试图分析间隙关闭过程中后牙横向移动的变化趋势，但由于三维有限元实验方法的局限，上述3个关闭阶段的牙齿移动均为加力后的初始位移，因此，这可能是本实验与其他临床研究差异的另一个原因。

第二磨牙无论实验组还是对照组均表现为牙冠颊向移动。对于实验组而言，第二磨牙牙冠颊向移动可能是因为关间隙过程中随着牙弓两侧加力，主弓丝沿后牙颊管向远中滑动，同时两侧第一磨牙受力带动TPA向近中移动，由直径为0.9 mm不锈钢丝弯制而成的TPA［19］具有一定的刚性，类似一个坚硬横梁支撑在第一磨牙间形成支点造成主弓丝发生形变，从而引起第二磨牙颊向移动；由于三维有限元分析方法尚不能模拟牙槽骨的改建，所有牙齿的移动均为牙周膜受力形变产生的初始位移［9，18］，而实验设置的牙周膜厚度仅0.2 mm［5-6］，因此，对照组第二磨牙的颊向移动可能是第二前磨牙、第一磨牙在间隙关闭过程中由于近中舌向移动超过牙周膜形变范围后受到舌侧骨壁的阻碍，产生类似TPA效应使主弓丝发生形变，从而导致第二磨牙的颊向移动。另外，与有限元研究不同的是，临床上随着第一磨牙的近中舌向移动，越隔纤维也会潜在地使第二磨牙近中移动［20］，这可能会抵消部分TPA效应引起的颊向移动。而主弓丝的尺寸大小与刚性及其与托槽系统间余隙角大小也可影响第二磨牙移动类型［5，21］。

虽然三维有限元方法通过建模可精确分析正畸过程中牙齿三维方向上的移动，但该方法目前仅能计算牙齿的初始位移，尚不能模拟牙槽骨的改建以反映牙齿的连续移动。目前研究滑动法关间隙过程中牙弓宽度变化的文献较少，使得本实验进行力值计算时困难程度加大，因此对关间隙各阶段的模型设置进行了简化，2、4 mm的模型为前牙整体后移，而临床关间隙过程中前牙存在一定程度的倾斜及后牙的前移。因此，三维有限元牙槽骨的连续改建将是课题今后的研究方向。

4 总 结

TPA的使用阻碍了滑动法关间隙过程中尖牙、第二前磨牙及第一磨牙间宽度的进一步减小，有利于维持牙弓形态的稳定，但有加大第二磨牙牙冠颊向移动的趋势，在间隙关闭过程中应注意第二磨牙的转矩控制及横向位置的调整。