一种机动目标动态规划检测前跟踪算法

孟 宁 史小斌 高青松 连 豪 任哲毅 孙藏安

(西安电子工程研究所 西安 710100)

0 引言

检测前跟踪(Track-Before-Detect，TBD)是低信噪比条件下对雷达微弱目标进行检测和跟踪的一种方法。和传统跟踪方法比较，这种方法对单帧的雷达回波数据不做目标检测宣判，而是对目标的多帧雷达回波信息进行累积，然后判决检测结果，并且同时完成雷达目标的跟踪航迹。由于对单帧回波数据没有进行过门限操作，TBD保留了更多的目标信息,所以TBD的实质是利用时间累积来提升雷达目标雷达信号信噪比[1-4]。

基于动态规划(Dynamic Programming，DP)的雷达微弱目标检测前跟踪算法最早在红外微弱目标的检测中进行应用，最近几年在雷达系统中也应用了该检测跟踪算法。在这些应用中，假设目标具有匀速直线或者弱机动的运动特性，由于跟踪目标速度变化比较小，采用雷达目标的起始速度确定动态规划方法里面每一帧的搜索范围，匹配跟踪目标的航迹，实现比较好的检测跟踪效果[5]。然而，当目标做比较大转弯机动时，由于目标速度(大小与方向)变化比较大，目标起始速度决定的状态转移步长不能每时每刻和雷达目标真实速度相匹配，这样就不能对雷达目标进行有效地检测和跟踪[6]。

文中首先采用状态转移矩阵实现雷达目标状态的预测，当对雷达目标的每个可能状态进行搜索时，采用相邻时刻状态之间距离差作为搜索窗的匹配速度，实现了沿着目标运动方向的目标信号能量的有效积累。该算法的优点是跟踪目标的转移步长在每时每刻变化，这对于跟踪转弯机动目标是必要的，由于转弯机动目标的速度在一直变化，需要不断地改变转移步长来匹配目标航迹。

1 目标运动模型

(1)

目标状态转移方程为：

Xk=FCV·Xk-1+QCV·Vk-1

(2)

其中，状态转移矩阵：

(3)

式(3)中：Ω表示目标转弯系数，Ω>0时雷达跟踪目标左转;Ω<0时雷达跟踪目标右转。线速度相等的条件下，Ω越大雷达跟踪目标转得越快。

过程噪声输入矩阵：

(4)

过程噪声：

Vk-1=[δx(k-1)δy(k-1)]T

(5)

2 自适应步长DP-TBD算法

假设量测平面有Nx×Ny个分辨单元，每个分辨单元的大小为Δ×Δ，第k时刻的量测数据Zk为一Nx×Ny矩阵，且有

Zk={zk(i,j)} 1≤i,j≤N

(6)

其中，zk(i,j)是k时刻分辨单元(i,j)的测量值。

(7)

其中，Ak表示点目标在分辨单元(i,j)处的信号强度；wk(i,j)是分辨单元(i,j)处的观测噪声，且满足均值为0、方差为δ2的高斯分布。

动态规划方法解决的核心问题为：从观测矩阵序列(Z1,Z2,…Zk)中寻找出雷达目标的状态矩阵序列(X1,X2,…Xk)。

2.1 传统动态规划检测前跟踪算法

传统DP-TBD算法流程如下：

(8)

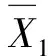
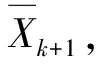
(9)

其中，q为有效状态转移数，取q=9。

步骤3：结束。根据门限VT找出满足条件的状态，有

(10)

其中，VT为检测门限。

步骤4：回溯。当k=K-1,K-2,…,1时

(11)

传统动态规划算法假定目标具有匀速直线或者弱机动特性，设定目标的初始速度，利用目标的初始速度确定动态规划算法每一帧的搜索范围，从而匹配目标的运动轨迹，达到较好的检测跟踪效果。

检测的航迹为利用检测前跟踪技术恢复的目标航迹。检测前跟踪是通过对多帧原始回波进行联合处理。图1为单帧回波过门限处理效果，可以看出噪声引起的虚警点很多；图2为两帧回波处理效果，虚警显著降低；图3为四帧回波处理效果，虚警已经很低。所以，联合处理回波帧数越多，对噪声抑制效果越好。

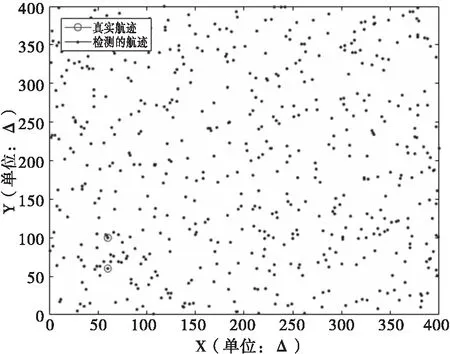
图1 单帧回波处理效果(K=1)

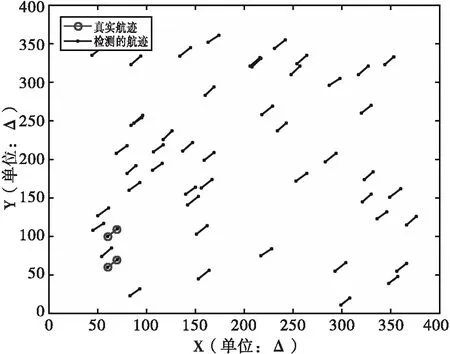
图2 两帧回波处理效果(K=2)

图3 四帧回波处理效果(K=4)

当目标做转弯机动时，搜索范围与目标模型不匹配，传统动态规划算法的性能会严重下降。如果加大搜索范围，算法的计算量会大幅度增加。如果能够在当前帧预测到目标在下一帧的大概位置，并改变转移步长，那么就可以检测到目标，提高检测性能。

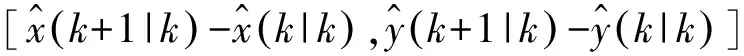
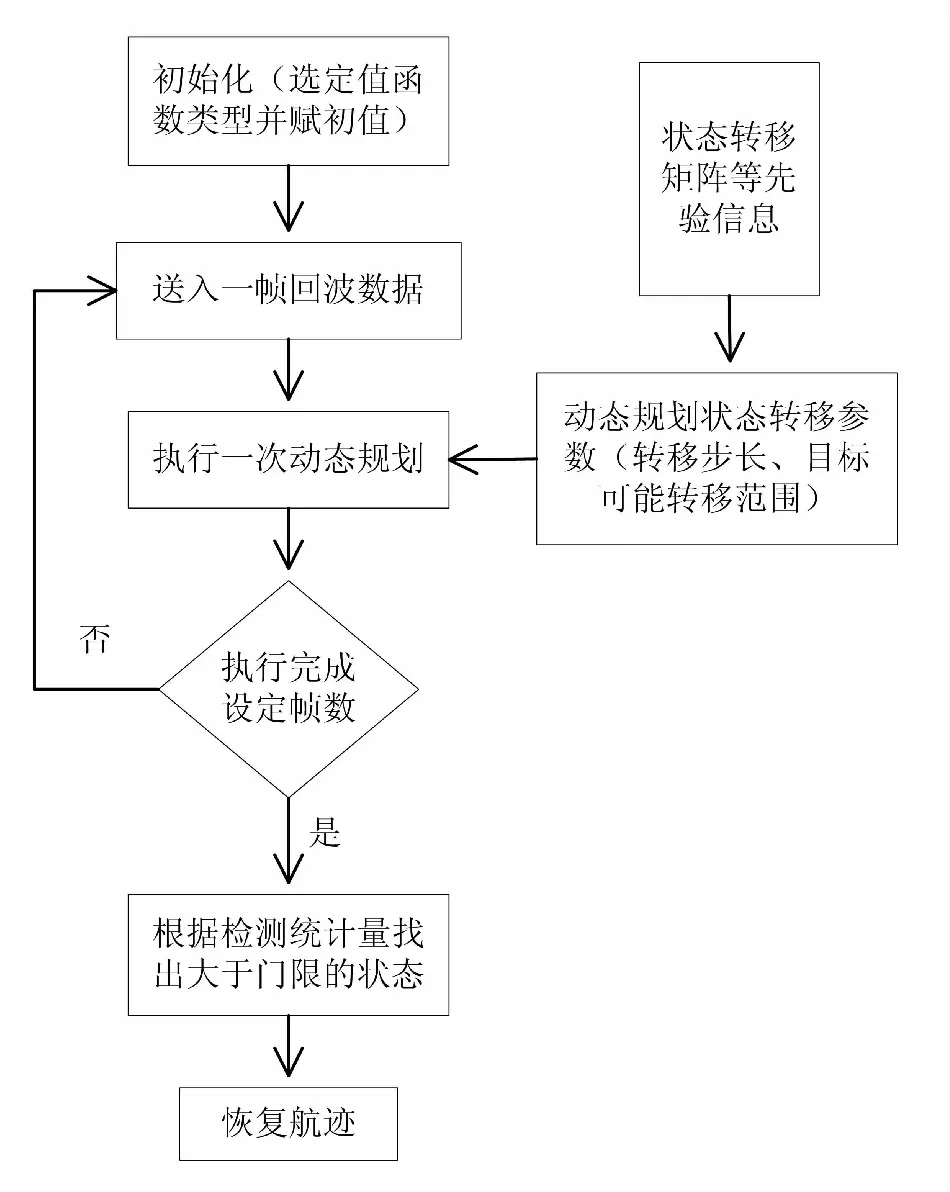
图4 算法流程图

2.2 变步长动态规划检测前跟踪算法

当目标做转弯运动时，搜索范围与目标模型不匹配，传统动态规划算法的性能会严重下降[8]。如果加大搜索范围或每相邻两帧通过滤波算法对速度实时更新，算法的复杂度和运算量都会大幅度增加。如果在当前帧能够估计出雷达目标在下一帧的大概位置，并实时改变状态转移步长，就能够提高雷达检测性能。

变步长动态规划具体算法流程为：

(12)

(13)

(14)

2)计算可变步长

①状态预测

(15)

②状态量化

(16)

(17)

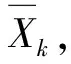
(18)

(19)

3)结束：根据门限VT，找出满足条件的状态。

(20)

4)回溯：当k=K-1,K-2,…,1时

(21)

3 仿真分析

对于目标做近匀转弯(CT)机动，为了验证该算法的有效性，将变步长DP-TBD算法与传统的DP-TBD、粒子滤波、IMM-EKF算法进行了性能对比，目标运动场景描述如下：

目标1从初始位置(60m,60m)以角速度ω=0.1rad/s做近匀转速运动，持续11s，观测间隔1s；目标2从初始位置(60m,150m)以角速度ω=0.1rad/s做近匀转速运动，持续11s，观测间隔1s。目标1和2的虚警率为10-3，过程噪声、观测噪声分别为强度为0.01和0.1的高斯分布。过低门限处理后目标运动场景如图5所示。

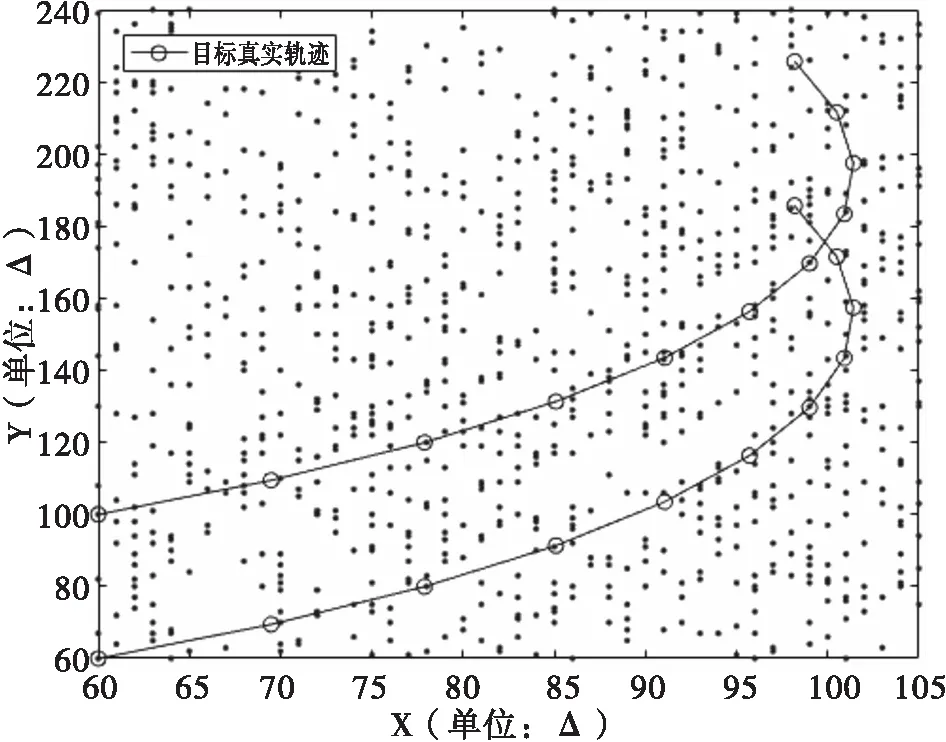
图5 目标运动场景(ω=0.1rad/s)

目标空间位置均方根误差为：

(22)

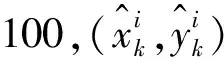
传统DP-TBD算法、变步长DP-TBD算法、粒子滤波和IMM-EKF算法对于近匀转弯弱机动(如ω=0.015rad/s)目标，均可达到良好的跟踪效果，见图6。从图7可以看出，传统的DP-TBD算法位置均方根误差可以达到4.7m，远远大于变步长DP-TBD算法、粒子滤波和IMM-EKF算法位置均方根误差；粒子滤波和IMM-EKF算法位置均方根误差次之；变步长DP-TBD算法位置均方根误差最小。

图6 目标实际轨迹和跟踪轨迹(ω=0.015rad/s)

图7 目标位置均方根误差曲线(ω=0.015rad/s)

航迹精确跟踪概率为对于恢复出的目标航迹满足每一帧的估计的目标位置与真实目标位置误差小于2个单元格。对于4帧数据，从图8可以看出当角速度ω>0.1rad/s时常规DP-TBD算法已经跟踪失效。不管ω为多大，变步长DP-TBD、粒子滤波和IMM-EKF算法的航迹精确跟踪概率均接近1。也就是说，对于近匀转弯强机动目标，变步长DP-TBD、粒子滤波和IMM-EKF算法可以实现目标跟踪，而传统DP-TBD算法跟踪失效。

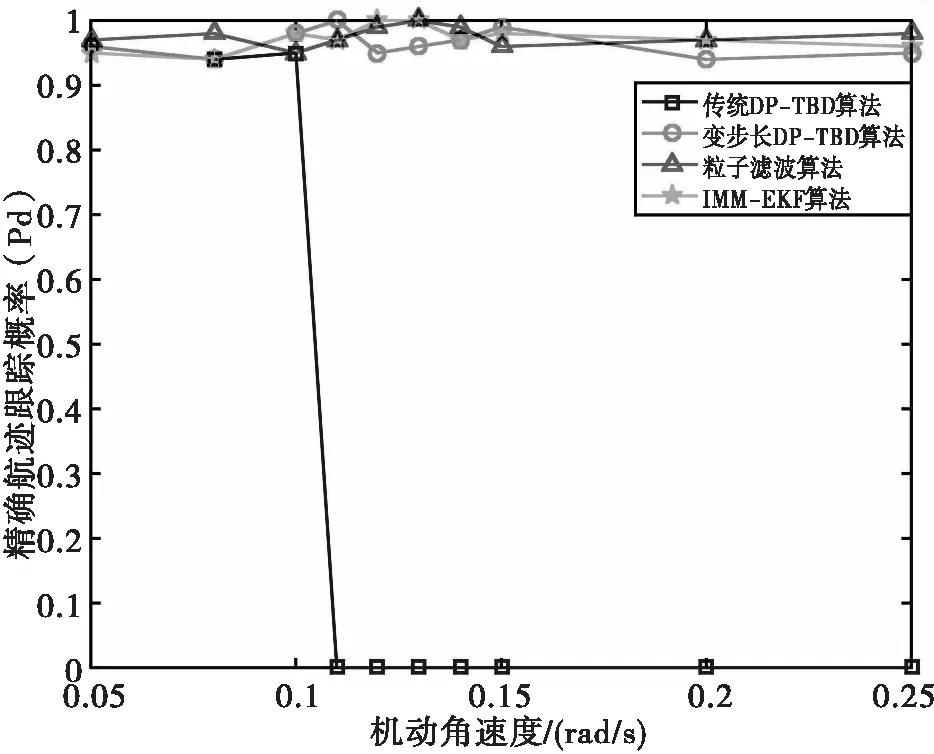
图8 精确航迹跟踪概率曲线(4帧累积)

图9和图10分别为近匀转弯强机动(ω=0.15rad/s)目标变步长DP-TBD算法目标值函数累积效果、目标真实轨迹和估计轨迹图，可以看出跟踪效果很好。

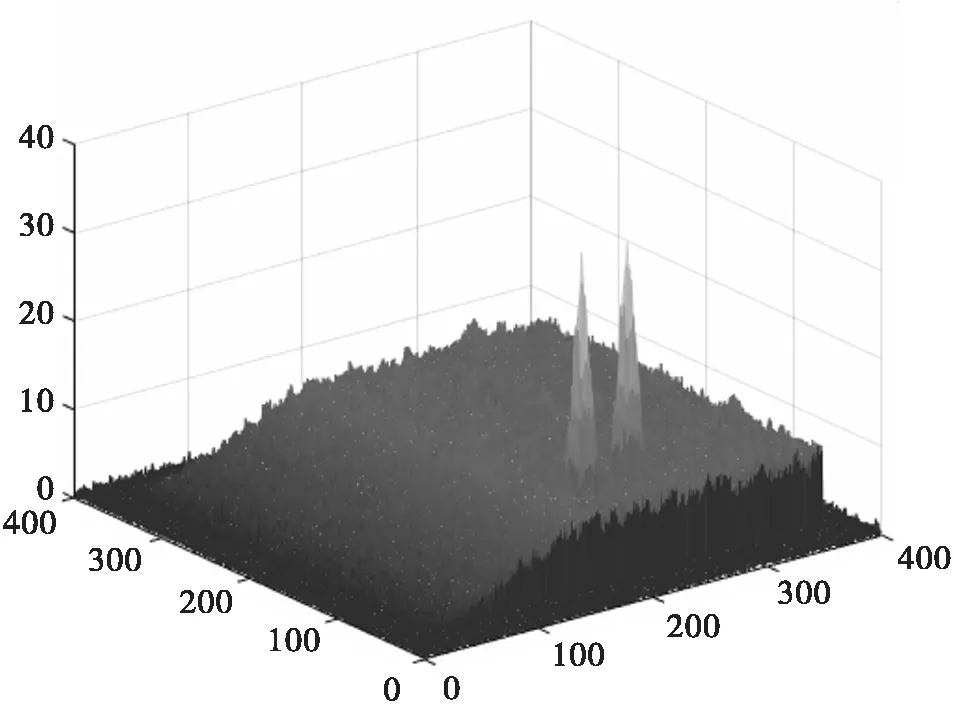
图9 变步长DP-TBD值函数累积图(ω=0.15rad/s)

图10 变步长DP-TBD目标真实轨迹和跟踪轨迹(ω=0.15rad/s)

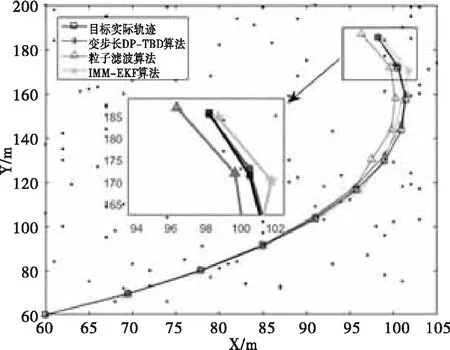
图11 目标实际轨迹和跟踪轨迹(ω=0.1rad/s)

从图11可以看出，变步长DP-TBD算法、IMM-EKF和粒子滤波算法对于近匀转弯强机动目标均可达到良好的跟踪效果。图12为目标空间位置均方根误差图，可以看出，粒子滤波算法航迹位置均方根误差最大，IMM-EKF算法次之，变步长DP-TBD算法最小。

图12 目标位置均方根误差曲线(ω=0.1rad/s)

综上，对于近匀转弯弱机动目标变步长DP-TBD、常规DP-TBD、粒子滤波和IMM-EKF算法均可以实现目标跟踪，且变步长DP-TBD算法跟踪精度最高。对于近匀转弯强机动目标，常规DP-TBD算法跟踪失效，而变步长DP-TBD算法、粒子滤波和IMM-EKF算法可以实现目标跟踪，且变步长DP-TBD算法跟踪精度最高。

4 结束语

针对传统动态规划检测前跟踪算法跟踪机动目标性能不理想的问题，本文利用目标状态转移矩阵先验信息改进了传统DP-TBD算法。该算法把下一时刻目标状态预测融合到动态规划算法，实现对雷达机动目标模型的动态预测，避免了雷达跟踪目标模型引起的搜索范围失效导致无法有效跟踪雷达机动目标的缺陷。仿真结果显示，变步长动态规划检测前跟踪算法在跟踪机动目标时的性能优于传统动态规划检测前跟踪算法，跟踪精度也比粒子滤波和IMM-EKF算法高。