一种基于卫星单天线的弹体伪姿态测量新方法

李耀军 李喜民 潘 泉 程晓冉

(1.西安电子工程研究所 西安 710100；2.西北工业大学 西安 710129)

0 引言

载体姿态信息是导航与制导领域不可缺少的信息。炮弹、榴弹、火箭弹等常规旋转弹药，在获得旋转稳定性的同时给弹姿测量带来了困难[1]，主要体现在量程、动态范围及测量精度，转速超过10Hz的情况，已将惯性导航排除在外，目前主流的测量组件是地磁类传感器，量程大，动态范围宽，然而不足之处在于精度低且受地磁场方向约束。常规弹药制导化是智能弹药的发展趋势[2]，无控弹药如能实时获取弹体的飞行姿态，以及电动舵机、气动舵机或者脉冲发动机的舵片的实时位置，基于事先设置的控制策略驱动执行机构舵偏角，及时改变弹体气动力，持续调整弹体位置逼近预置弹道，实现弹道修正与精确控制，进而实现精确打击[3-5]。由此可见，如何获取常规弹药的飞行姿态直接关系到常规弹药的精确制导能力[6-7]。

长基线卫星姿态测量系统[6]具有高精度位置和姿态测量优势。多天线卫星姿态测量技术目前已经比较成熟[7-8]，已进入工程应用阶段；同时，基于多天线卫星测姿系统天线阵列结构复杂、安装要求较高、重量、体积、功耗及成本都难以满足低成本制导弹药的要求，极大地限制了卫星导航与测姿技术在智能弹药方面的应用[8-9]。

探索单天线卫星导航与测姿新技术，将基于运动学原理开展弹体姿态测量技术研究。作为基于载波卫星导航与测姿技术的补充和备份[9-14]，面向制导弹药二维弹道修正执行机构对弹体姿态的需求，运用弹体运动学原理，在不引入惯性测量单元、地磁等其他传感器的情况下，基于传统卫星导航接收机输出的速度信息，在弹体飞行攻角和侧滑角较小的情况下，实现了弹体三维姿态运动学建模，由于通常情况下攻角和侧滑角难以给出，计算的姿态即称之为伪姿态，其测量精度能够满足常规弹药制导化需求。

引入伪姿态[9-14]的概念，分析了由伪姿态测量辅助求取载体姿态的具体算法，建立了单天线卫星姿态测量的数学模型，通过设计相应的滤波器对状态参数进行估计，得到相应伪姿态信息，根据常规姿态与伪姿态的关系，得到常规姿态信息。

1 单天线伪姿态测量

1.1 伪姿态测量

根据弹体应用实际条件，相关坐标系，如载体坐标系(Obxbybzb)、地理坐标系(Otxtytzt)、风轴系(Owxwywzw)、稳定坐标系(Osxsyszs)及常规姿态和伪姿态的定义参见文献[18]。基于上述坐标系定义及载体姿态约定，给出载体伪姿态的解算模型[19]。

假设已知速度矢量为

v=vei+vnj+vuk

(1)

则，加速度矢量为

a=aei+anj+auk

(2)

如图1所示伪姿态角之间的几何关系，可得伪偏航角ψs计算公式为

ψs=arctan(ve/vn)

(3)

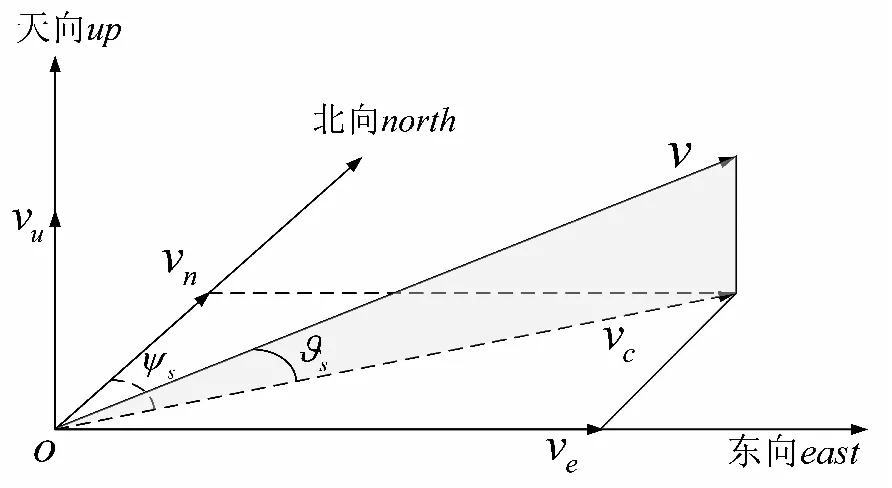
图1 伪姿态角之间的几何关系

同时，易得伪俯仰角ϑs计算公式为

(4)

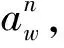
(5)

图2 加速度与各矢量之间的关系

滚转角与各矢量之间的关系如图3所示，则伪滚转角计算公式为

(6)

图3 滚转角与各矢量之间的关系

1.2 计算流程

卫星导航接收机在接收到卫星信号后，通过一系列导航解算处理后，得到载体的位置和速度信息；地理坐标系下的速度分量信息通过卡尔曼滤波处理得到稳定的东、北、天方向的加速度分量；然后，基于速度分量信息和加速度分量信息进行伪姿态信息的解算，求取载体的伪偏航角、伪俯仰角和伪滚转角。最后，对计算得到的载体姿态信息，进行优化处理，以提高姿态信息的精度。整体方案如图4所示。

图4 单天线GPS姿态测量系统结构图

1.3 状态估计

在地理坐标系下速度v={ve,vu,vn}已知的情况下，其对应的加速度a={ae,au,an}可以通过构建三个独立的卡尔曼滤波器估计出来，下面将以东向为例构造卡尔曼滤波器。

假设k时刻xe(k)的东向分量为

(7)

设k+1时刻状态[10]

xe(k+1)=Φxe(k)+z(k)

(8)

其中，Φ为转移矩阵，z(k)为系统噪声。

构建状态观测方程

ye(k)=Hxe(k)+v(k)

(9)

其中H为观测矩阵，只计量速度，写为

H=[1 0 0]T

(10)

至此，完成东向速度分量与加速度分量的滤波器设计，相关计算公式如下

其中，Q为系统噪声，R为观测噪声。同理，计算出北向和天向的相关状态分量。

1.4 矢量计算

卫星接收机输出速度v和高度h，可差分出偏航角λ，由此可得东向及北向速度

(12)

速度分量vu可通过差分方式获得

vu=[h(k+1)-h(k)]/Δt

(13)

假设地理坐标系下加速度为a={an,ae,au}，可通过对速度的北向分量进行差分，计算出加速度的北向分量

an=[vn(k+1)-vn(k)]/Δt

(14)

同理，计算出其他加速度分量，则

a=ani+aej+auk

(15)

1.5 姿态变换

若已知坐标系旋转角α,β，可根据变换矩阵[20]由伪姿态计算出常规姿态，计算公式如下所示。

地理坐标系变换到稳定坐标系的方向余弦矩阵，记为R(ψs,ϑs,γs)

R(ψs,ϑs,γs)=

(16)

稳定坐标系变换到载体坐标系的方向余弦矩阵，记为L(α,β)

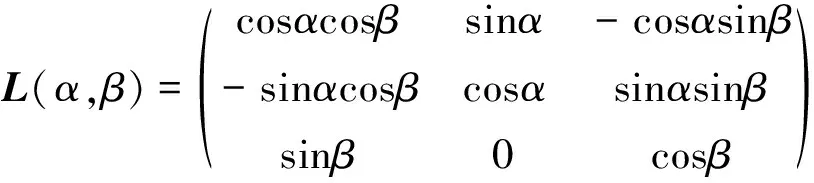
(17)

地理坐标系变换到载体坐标系的方向余弦矩阵，记为R(ψ,ϑ,γ)

R(ψ,ϑ,γ)=L(α,β)R(ψs,ϑs,γs)

(18)

(ψ,ϑ,γ)即为常规姿态。

1.6 优化计算

对求得的姿态信息进行优化处理。尝试了采取α-β滤波及高斯牛顿迭代法进行姿态信息的优化计算。

1)α-β滤波

建立估计方程

(19)

式(19)中，xp(k+1)为位置估计值，vp(k+1)为速度估计值，T为量测周期。

则，xs(k)与vs(k)可计算如下

(20)

式(20)中，xm(k)为实时量测。

2)高斯牛顿迭代法

高斯牛顿迭代法是非线性最小二乘的一种优化算法，采用逐步迭代的方法，把非线性问题变成一步一步迭代的线性问题，从而达到极值收敛。算法步骤如下：

①确定目标函数；

②选取初值，将解算的初始时刻的姿态信息选为迭代初值；

③对第k次迭代计算雅克比矩阵及增量Δxk=(JTJ)-1JTε(xk)；其中，J为雅可比矩阵，ε(xk)为第k步时的残差，Δxk是第k步时的增量；

④若增量Δxk小于规定的精度值，则停止迭代。否则，更新xk+1=xk+Δxk；

⑤循环执行步骤②及步骤③直到满足终止条件或达到最大循环次数。

2 实验测试与分析

2.1 实验流程

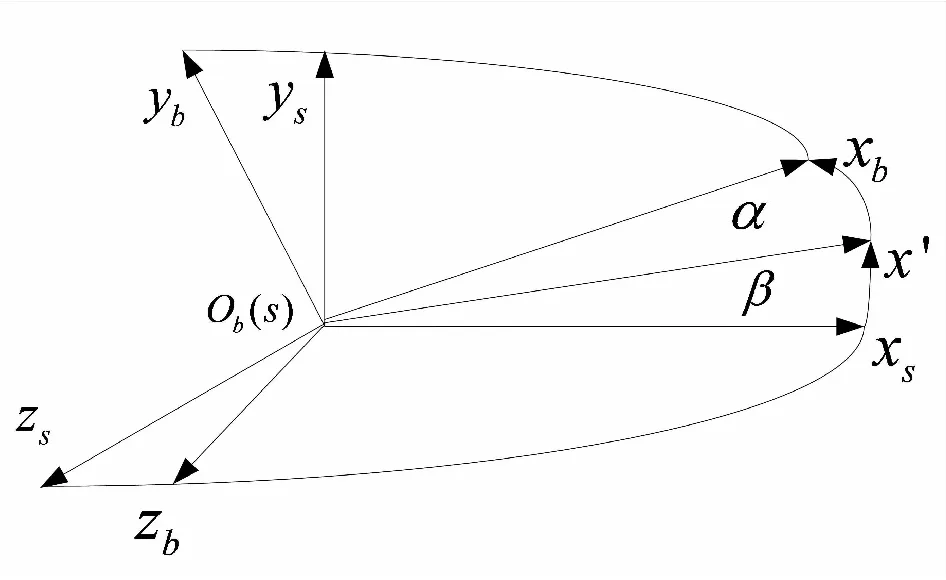
图5 稳定坐标系与载体坐标系之间的关系

为验证算法的可行性和有效性，对某火箭弹单天线卫星测姿系统进行实验分析。整个仿真流程如图6所示。

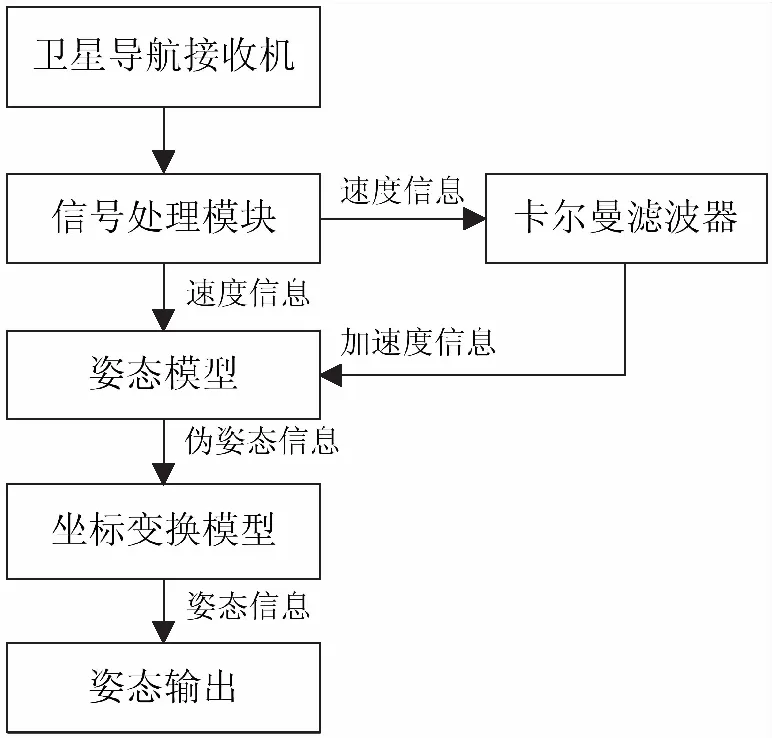
图6 单天线测姿实验流程图

1)将卫星输出的速度数据进行矢量化处理，并分离出速度信息，该速度信息作为输入量为卡尔曼滤波器所用，通过滤波估计，得到载体的实时加速度；

2)速度与加速度信息作为伪姿态模型的数据输入，通过箭体计算机实时运算可求取载体的伪姿态；

3)根据式(20)可求取常规姿态角(ψ,ϑ,γ)。

2.2 实验结果及分析

对实验数据进行算法验证，由从GPS解算的信息中，得到三个方向的速度，即东向速度，北向速度，和天向速度，通过伪姿态算法对姿态信息进行解算与处理，将处理后的姿态信息，与真实姿态信息做比较，得到姿态的误差角度，以验证该算法的有效性。

1)无人机挂飞实验一组

①偏航角实验测试

从挂飞数据的可以看出测姿误差范围都在±10°。在处理姿态信息时存在初值选取的问题，这是其弊端之一，如果初值的选取不合适，那么结果将会收敛到另外一个值上，甚至会引起结果的发散。实验结果如图7所示。

②俯仰角实验测试

从挂飞数据的俯仰角实验结果来看，高斯牛顿方法与α-β滤波方法的效果基本没有差别，两种方法的误差都在±10°之间。同样，高斯牛顿法存在初始值的选取问题，结果如图8所示。

③滚转角实验测试

使用高斯牛顿方法处理数据，滚转角在一个较大的范围内波动，若初值选取不合适，则无法收敛到合适的值上。从实验结果里看，使用α-β滤波方法处理后的姿态信息更加平稳。从两种方法的误差来看，高斯牛顿方法的误差范围在±10°，α-β滤波方法处理后的数据误差范围在±8°，两者有一定差别，但并不明显。两种方法的处理时间仍是高斯牛顿方法所需时间大于α-β滤波所需时间，多次实验所得结论一致。实验结果如图9所示。

图8 无人机挂飞实验俯仰角测试结果

图9 无人机挂飞实验滚转角测试结果

2)无人机挂飞实验二组

无人机挂飞实验二组实验结果如图(9)所示。从无人机挂飞实验二组实验结果来看，在偏航角的信息处理中，两种方法得到的结果近乎近似。在俯仰角的信息处理中，高斯牛顿方法相比α-β滤波方法更好一点，但不明显，两者的误差范围都在-10～10°。在滚转角结果中，高斯牛顿方法相比α-β滤波方法较差，高斯牛顿方法的误差在-10～10°，α-β滤波方法误差在-6～6°。总体来看，本组实验与无人机挂飞实验一组所得结论一致，实验结果如图10所示。

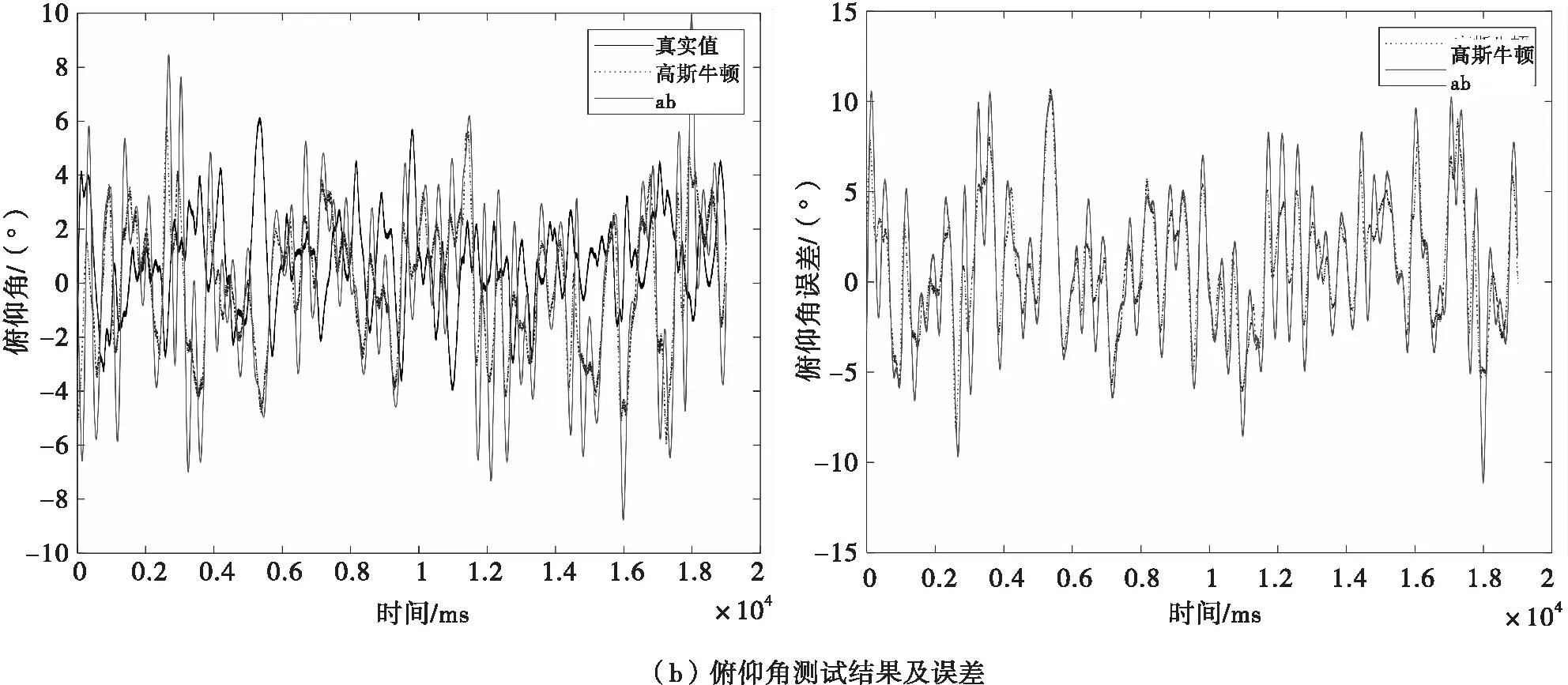
图10 无人机挂飞实验偏航、俯仰、滚转角测试结果

3 结束语

利用单天线卫星测姿技术破解卫星导航在旋转弹上无法测姿的难题，可以用较低成本同时提供位置和姿态信息，具备弹姿/弹道一体化测量功能，替代惯性导航及地磁传感器，在增强卫星制导组件的功能和性能的同时，大幅提高制导组件耐高过载能力及可靠性，也将大幅降低二维制导组件成本，具有较强的实际应用价值。