基于时频分析的灵巧干扰特征研究

李辰梓 余建宇 徐 伟 郝万兵

(西安电子工程研究所 西安 710100)

0 引言

雷达干扰是指通过将干扰信号随同敌方期望收到的信号一起送入敌方接收机中，当干扰信号强到足以使敌方无法从中提取到所需信息时，干扰就是有效的[1]。传统的雷达干扰按照原理分为压制性干扰和欺骗性干扰，压制性干扰是指用噪声信号或噪声调制的强干扰信号遮盖或淹没目标回报信号，使雷达无法从中检测目标的信息。欺骗性干扰即产生假的目标和信息，使雷达无法正确地检测真实的目标，从而达到迷惑和扰乱雷达对真正目标检测和跟踪的目的[2]。

现代新体制雷达为了对抗干扰，雷达信号一般都采用了脉内或脉间相干的信号波形，最常见的信号形式为线性调频信号。传统噪声干扰采用非相参噪声调制产生的干扰信号，经雷达端接收进行脉冲压缩后，噪声信号能量大部分被滤除，使干扰效果大大减弱。并且当前雷达大都采用旁瓣消隐(SLB)和旁瓣相消(SLC)等抗干扰措施，使得传统的干扰样式不能够产生干扰压制或者假目标欺骗的效果。因此为了应对这些新的抗干扰措施而提出了灵巧干扰这一概念，它同时具有欺骗干扰和压制性干扰的特点。由干扰机将截获的雷达信号进行存储并调制产生灵巧干扰信号，因此干扰信号可根据被干扰对象灵活变化与雷达发射信号相匹配，使干扰能够获得理想的相参积累增益，增强了可利用的干扰能量。

本文以LFM雷达信号为研究对象，对卷积调制灵巧噪声干扰以及间歇采样转发干扰进行了研究仿真分析，并对不同形式干扰信号的时频和域特征进行研究，为后续干扰及抗干扰提供先验信息。

1 灵巧干扰

灵巧干扰的提出是为了应对如何有效干扰采用脉内或脉间相干波形的新体制相参雷达。首先对侦收的目标雷达信号利用数字射频存储技术(DRFM)进行完整无失真的保存，然后对存储的雷达信号进行调制产生期望得到的灵巧干扰信号[3]。干扰信号本质上是雷达自身信号进行调制转发，因此产生的干扰波形与雷达具有较好的相干性，信号大部分能量能通过相参雷达的检测脉压系统，对相参雷达产生有效的干扰[4]。

1.1 卷积调制灵巧干扰样式

卷积噪声干扰是将干扰机通过侦收天线将接收到的雷达信号经过滤波、放大后进行存储，然后经过调制器将视频噪声信号与存储的雷达信号作卷积，经功率放大器放大后将信号进行发射的干扰方法[5]，图1为基于DRFM的卷积调制灵巧干扰方法原理框图。

图1 灵巧噪声卷积调制方法原理框图

干扰机侦察接收到的雷达信号为s(t)，干扰机选取的视频噪声信号为n(t)，干扰系统调制产生的卷积干扰信号为y(t)=s(t)*n(t)。噪声卷积干扰使用视频噪声与雷达本身信号的卷积结果作为干扰信号，只要雷达信号在干扰机的瞬时带宽内变化，干扰信号频率也会随之变化。也就是说干扰机不需要测频和频率引导，就能自动瞄准信号频率从而具有很好的相参性，因此这种干扰方法也能对频率捷变雷达进行干扰。干扰信号发射进入雷达接收机进行脉压处理为：

Y(t)=y(t)*s*(t)=s(t)*n(t)*s*(t)

(1)

设s(t)，n(t)，Y(t)的频谱分别为S(f)，N(f)，Y(f)，可得：

Y(f)=N(f)·|S(f)|2

(2)

进行变化可得到：

Y(t)=n(t)*F-1[|S(f)|2]

(3)

式(3)中,F-1表示逆傅里叶变换，F-1[ |S(f)|2]称作点扩展函数[6]。任何函数与点扩展函数卷积都可以获得脉压处理的增益，进一步印证了灵巧干扰对相参雷达干扰的有效性。

1.2 间歇采样循环转发灵巧干扰样式

间歇采样转发干扰目前国内外已经有大量的研究与应用，按照不同的脉冲间歇采样参数和转发方式，可以在真实目标附近产生假目标群，能有效地掩盖真实目标，在工程上对现有收发隔离式干扰机较易实现。本文研究中采用间歇采样循环叠加转发干扰的方式，其原理框图如图2所示。

图2 间歇采样循环转发干扰原理图

可以看出间歇采样循环转发灵巧干扰样式产生的干扰信号完全是对雷达信号进行复制和循环转发，与卷积调制样式最大的区别在于不需要额外的选用视频噪声来对雷达信号处理。所以本文选取卷积调制干扰和间歇采样循环转发干扰这两种典型的灵巧干扰样式进行仿真建模，对两类灵巧干扰信号的时频特性以及干扰效果进行研究分析，有利于从中研究对抗灵巧干扰的方法以及如何提高灵巧干扰的效果。

2 时频分析

时间t和频率f是信号分析和处理中两个很重要的变量，但时间域分析信号无法看出特定时刻信号的频率值，通过傅里叶变换在频率域也无法得到特定频率分量在时间上的准确分布。这时便要使用时间和频率的联合函数变换来分析信号，即时频域分析。时频变换主要分为两类，即线性时频变换和非线性时频变换。典型的线性时频变换有短时傅里叶变换，典型的非线性时频变换有Wigner-Ville分布。

Wigner-Ville时频分布是首先由Wigner提出用于量子力学领域，后由Ville引入信号分析而称之为WVD。该分布为其他时频分布的研究提供思路，信号分析和处理中，已成为了非常有用的工具，Wigner-Ville分布的表达式如公式(4)：

(4)

Wigner-Ville分布可以看作是一种用信号自身作为窗函数的特殊的STFT形式，这种窗函数实际上对信号具有某种程度的自适应性使得它的信号能量聚集性很好，但是在同时多信号的情况下Wigner-Ville分布会出现较为严重的交叉干扰项，使正确截获、分析信号变得非常困难。因此论文采用 WVD 的平滑形式，即Choi-Williams 分布(CWD)作为离线的信号的描述方法。CWD属于Cohen类分布，它是由Wigner-Ville分布通过与不同的核函数卷积产生[7]，其表达式如公式(5)所示：

(5)

Choi-Williams分布使用的核函数偏重于抑制远离原点的交叉项，这种特征对于大多数脉内调制信号来说是适用的，因此选来对于由雷达脉内调制的干扰信号进行时频域分析。

3 灵巧类干扰样式的仿真及时频分析

本次仿真条件设置如下，雷达信号S(t)选用线性调频信号，数学表达式如公式(6)所示：

(6)

其中信号时宽T为60μs，带宽B设置为20MHz，中心频率f0为50MHz，对雷达信号的采样率设置为100MHz。仿真得到雷达信号S(t)的时域图像、频域图像、经过雷达匹配滤波后产产生的脉压图像和时频域分析图像如图3、图4所示。

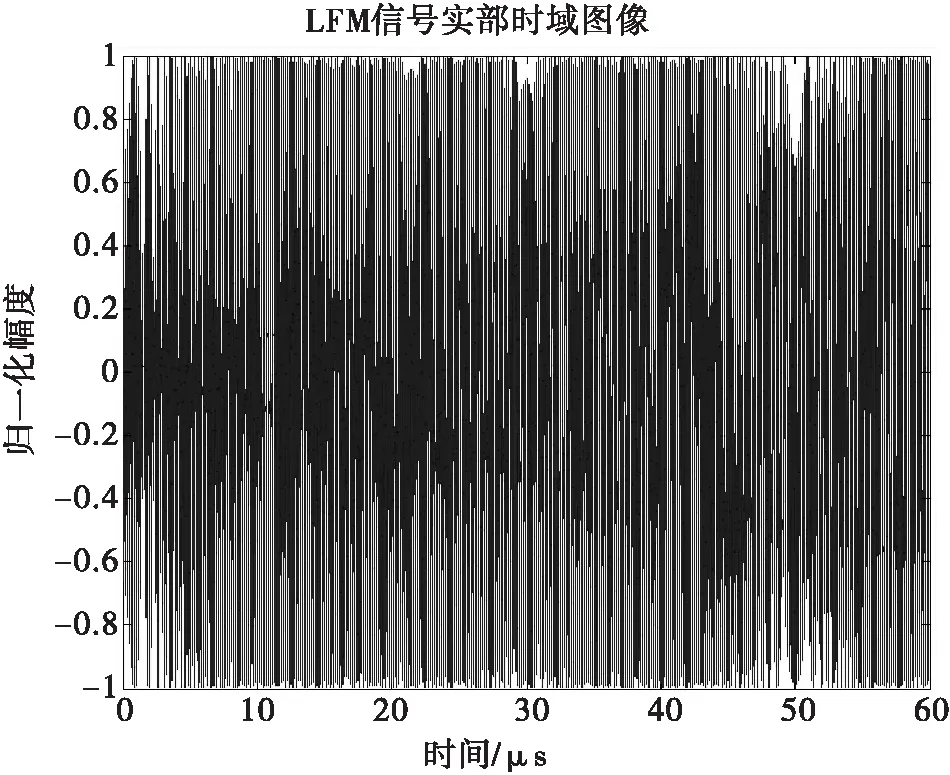
图3 LFM信号时域图

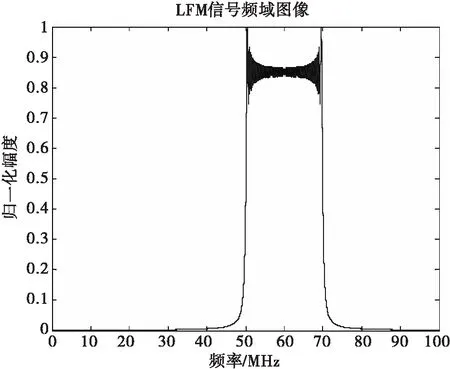
图4 LFM信号频域图

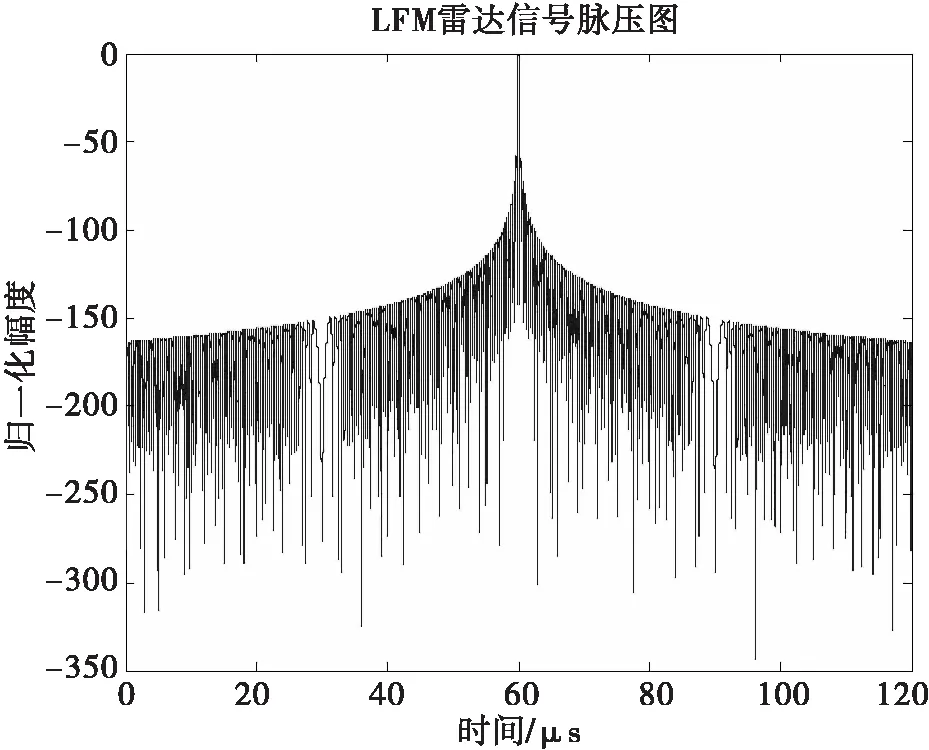
图5 LFM信号脉压图

图6 LFM信号CWD图

由图6中CWD图可以清楚地看到LFM信号时间-频率的对应关系，频率在50MHz～70MHz随时间线性变化，能准确的捕捉信号的时频特征。

3.1 卷积噪声灵巧干扰仿真

3.1.1 视频噪声为高斯白噪声

选用均值为0，方差为1，时宽为10μs的高斯白噪声信号作为视频噪声信号。

图7 灵巧噪声时域图

图8 灵巧噪声频域图

由图8可以清楚地看出灵巧噪声信号的的中心频率、带宽很好地对准了线性调频信号的中心频率和带宽(50MHz～70MHz)，能够造成良好的干扰效果。图9可以看到灵巧噪声信号通过雷达接收机的匹配滤波后出现了遮盖波形，能够遮盖住本身的雷达信号，产生了压制干扰的效果。并且经过多次仿真可以得出，选用的高斯白噪声时宽越宽，匹配滤波后压制干扰效果也会更好。

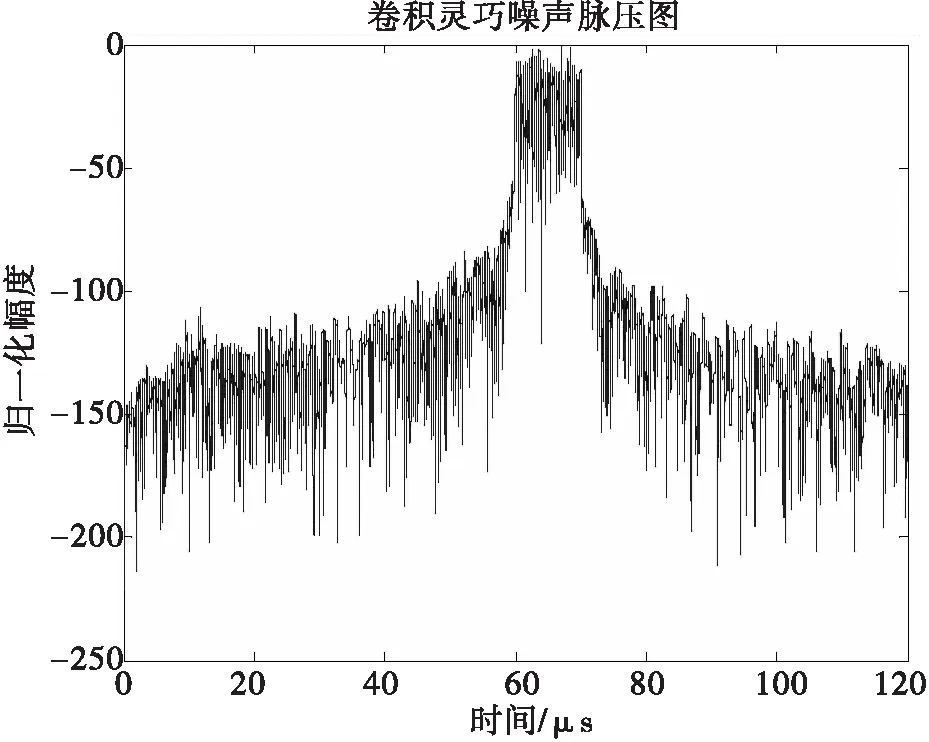
图9 灵巧噪声脉压图

图10 灵巧噪声CWD图

通过Choi-Williams分布对干扰信号视频分析得到图10，高斯白噪声产生具有高斯分布特性，但通过卷积干扰能够自动瞄准LFM信号频率，所以产生的灵巧干扰信号在时频域准确地遮住了LFM信号，能够很好地产生压制干扰效果。

3.1.2 视频噪声为矩形连续脉冲

n(t)选用为周期方波信号，参数设置为脉宽2μs，周期4μs，持续时间为40μs，幅度为1。

矩形脉冲与LFM信号卷积，等价于将LFM信号分别移位至每个矩形脉冲的位置，因此，卷积结果相当于不同延时的线性调频信号的叠加。并且由图13可以看出干扰结果产生了多个压缩峰，其间隔均小于线性调频信号的脉宽，达到了要求产生脉内高密度假目标的目的。由图14时频分析图可以看出矩形方波卷积灵巧干扰产生的假目标在时间上分布均匀，频率域完整地保留了LFM信号的全部信息，且产生的假目标幅度大致相同。

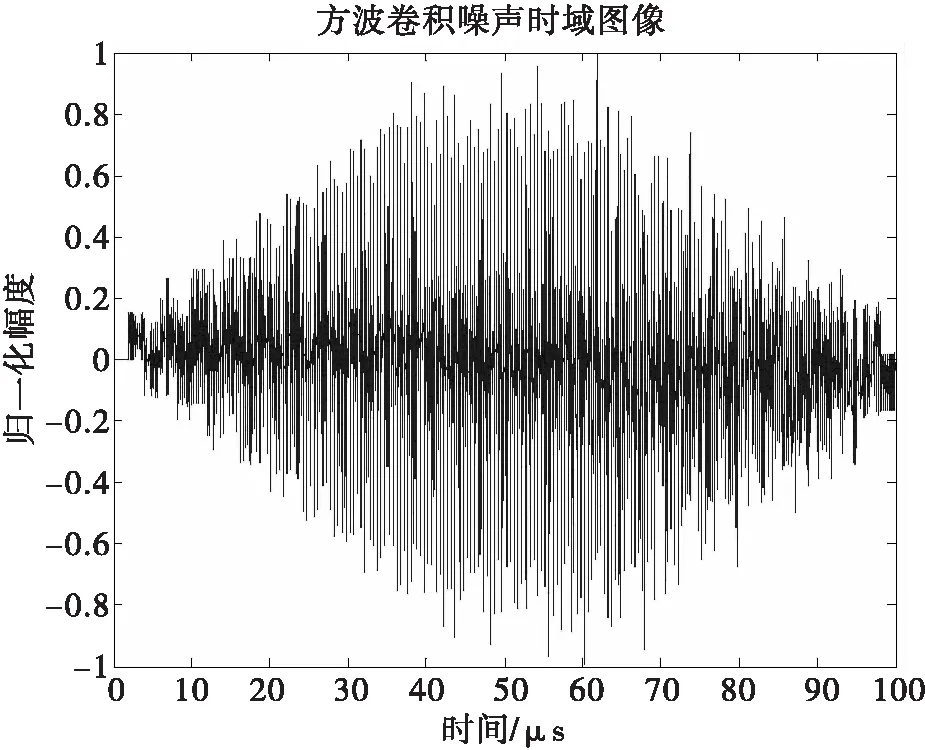
图11 灵巧噪声时域图

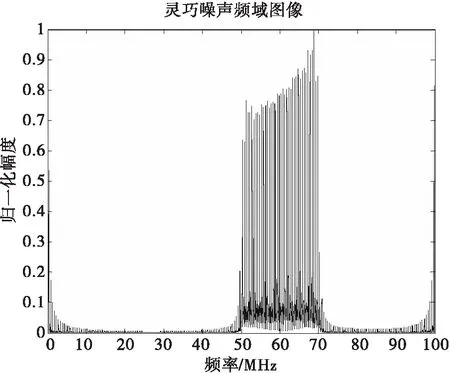
图12 灵巧噪声频域图

图13 灵巧噪声脉压图

图14 灵巧噪声CWD图

这些密集的假目标将会淹没真实目标或使被干扰雷达的处理能力饱和,从而使雷达不能准确地捕捉目标。根据多次仿真发现，改变矩形脉冲串中脉冲的个数，会影响假目标的数量，脉冲数目越多，产生的假目标就越多，密度就越大，干扰效果越好。但此种干扰产生的假目标间隔均匀，幅度基本一致，也可以用此特性来进行抗干扰处理。

3.2 间歇采样循环转发干扰

仿真中对LFM雷达信号S(t)进行间歇采样循环转发，一个采样转发周期为5μs，每次采样雷达信号之后，在一个周期剩下的时间内，转发的信号为之前存储的信号与当前采样信号的叠加，仿真结果如图15所示。

图15 循环转发干扰时域图

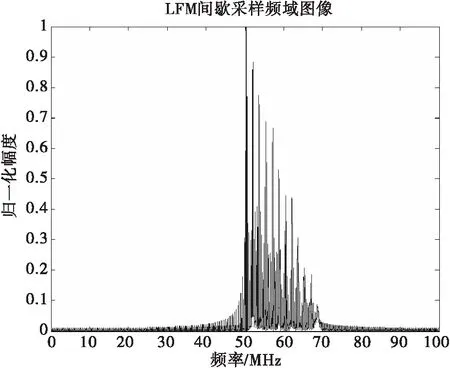
图16 循环转发干扰频域图

图17 循环转发干扰脉压图

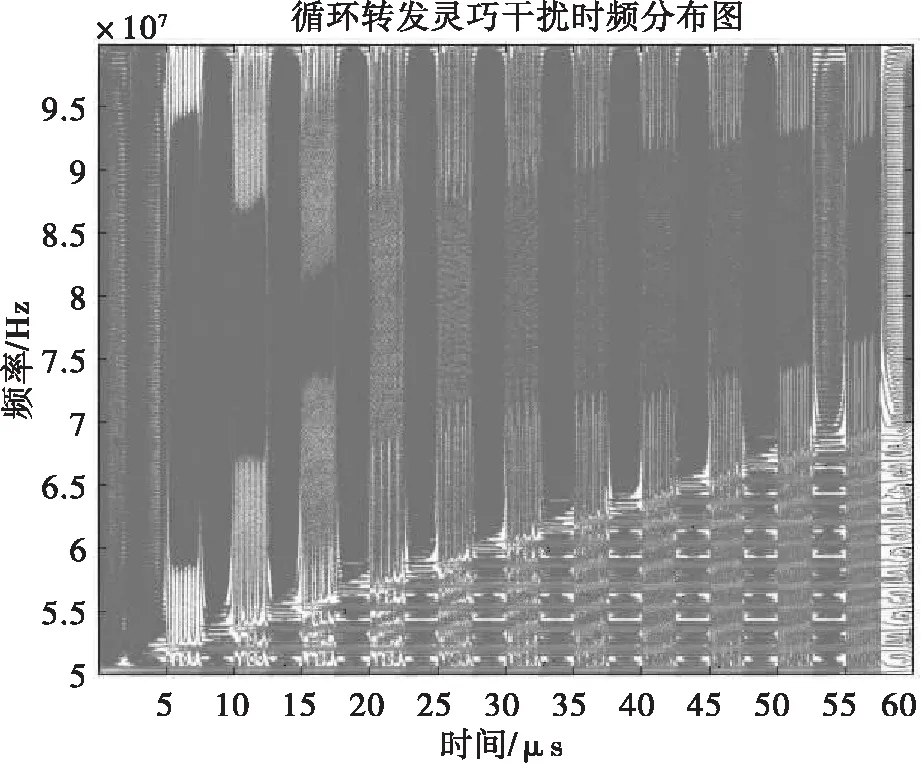
图18 循环转发干扰CWD图

从干扰信号频域图16和脉压图17可以看出，干扰信号本身是雷达自身信号的转发，干扰信号频率对准LFM信号，因此干扰具有较高的相参性，能够产生较好的干扰效果。从图18时频分析CWD图可以看清楚地看出，随着采样时间的推移，当前的干扰信号是由当前采样的LFM信号与之前所有采样LFM信号的叠加，包含之前采样得到所有信号的全部信息。并且通过多次仿真发现通过改变一个采样转发周期的速率，可以改变产生假目标的密集度，采样转发速率越高，形成的假目标数目就越密集。但是通过时频分析图也可以看出间歇采样循环转发干扰信号在整个脉冲持续时间内是非连续的，因此该特性可以被用来实现间歇采样转发干扰信号的识别和抑制。

4 结束语

灵巧干扰兼有欺骗干扰和压制性干扰的特点，并且实现具有很大的灵活性，在未来电子对抗中会发挥出越来越重要的作用。本文对卷积类灵巧干扰和间歇采样循环转发干扰建模，仿真研究改变干扰参数设置对干扰效果的影响，并且采用时频分析Choi-Williams分布来提取出干扰信号的时频域特征，有利于进一步优化灵巧干扰的干扰效果，使其在电子对抗中有更广阔的运用。