关于家禽类种群的数学经济模型建立及动力学分析

由 悦,张 雪

(吉林师范大学 数学学院,吉林 长春 130000)

0 引言

Smitch在对人类开发捕获渔业生物资源活动研究中,把经济问题和鱼类生物资源的数量问题相结合,提出了渔业自反馈模型[1]:

(1)

在渔业自反馈模型中考虑到产出的一种生物资源,即捕获的渔业资源.然而本文在此基础上考虑到一类具有两种生物资源产出的种群，如具有产蛋能力的家禽类种群,它们不仅可以满足人们对其食肉的要求,而且也可以达到其蛋类对市场供应的目标.于是建立了如下的生物数学经济模型:

(2)

其中:

E(t)为t时刻家禽类种群的密度;

F(t)为t时刻经营者获得的最大利润;

r为家禽类种群的内禀增长率;

K为环境的最大容纳量;

a为市场对家禽类种群的购买系数;

p为家禽类种群的市场价格;

q为家禽类种群产出品的市场价格;

b为市场对家禽类种群产出品的购买系数;

α为家禽类种群的产出系数;

c为单位家禽类种群的养殖成本.

其中r,K,a,,p,q,b,α,c均为正常数.下面将对系统(2)进行定性分析.

1 系统分析

鉴于此模型的生物学实际意义,我们在区域D={(E,F)|E≥0,F≥0}中考虑这个模型.令

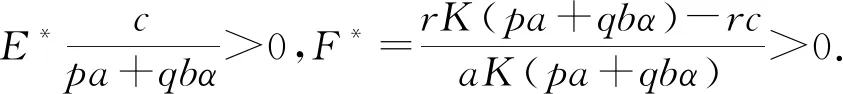
将系统(2)改写成

(3)

其Jacobi矩阵为:

记

ψ=-(a11+a22),φ=a11a22-a12a21,Δ=ψ2-4φ

而

定理1系统(2)的平衡点A(0,0)为鞍点.

证明 平衡点A(0,0)的Jacobi矩阵为:

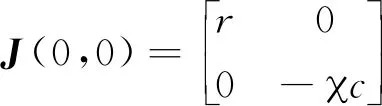
那么

ψ=-(a11+a22)=-(r-c),

φ=a11a22-a12a21=-rc<0,

故平衡点A(0,0)为鞍点.

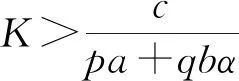
证明 平衡点B(K，0)的Jacobi矩阵为:

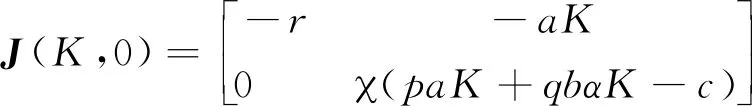
那么

ψ=-(a11+a22)=-[-r+(paK+qbαK-c)]=

r-(paK+qbαK-c)=r-[K(pa+qbα)-c]

φ=a11a22-a12a21=-r(paK+qbαK-c)-0=

-r(paK+qbαK-c)=-r[K(pa+qbα)-c]

则

Δ=ψ2-4φ={r-[K(pa+qbα)-c]}2+4r[K(pa+qbα)-c]=

{r+[K(pa+qbα)-c]}2>0.

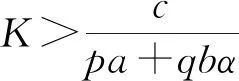
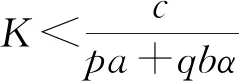
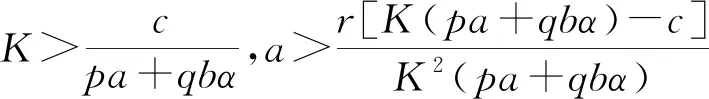
证明 1)先证正平衡点C(E*,F*)的存在性,唯一性.

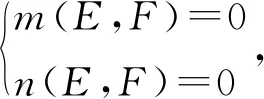
由第二个方程n(E,F)=0得:

将其代入第一个方程m(E,F)=0得:

引入辅助函数

且

即

f(0)>0.

又因为

即

f(K)<0.

由零点定理可知:至少存在一个ξ(0，K),使得f(ξ)=0.从而系统(2)存在唯一的正平衡点C(E*,F*)[3].

又因为f′(F)=a<0,所以f(F)是关于F的单调递减函数,故ξ在区间(0,K)上是唯一的.

2)再证平衡点C(E*,F*)是局部稳定的.

正平衡点C(E*,F*)的Jacobi矩阵为:

整理方程组

可得：

则

即ψ>0.

aE*F*(pa+qbα).

即φ>0.

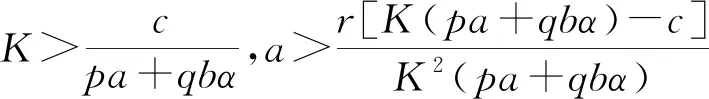
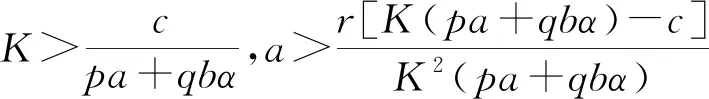
证明 选取Dulac函数B(E,F)=E-1F-1,经计算得:

所以

由Dulac判据[4]知系统(2)不存在位于D内的封闭轨线,即在系统(2)中不存在极限环.

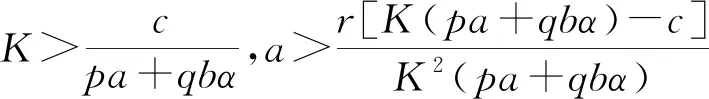
证明 由定理3知正平衡点C(E*，F*)是局部渐进稳定的,又由文献[5]中全局稳定性给出的定理2.2及推论2,可知C(E*，F*)是全局渐进稳定的.

2 主要结果的生物经济学意义

通过对系统(2)的定性分析,我们可以得到家禽类种群密度和经营者最优利益的数量C(E*,F*)，这一结果将为经营者的正确管理提供有价值的指导意义.当种群密度大于或小于E*时，经营者为了使其获得的利益最大化，就可以人为地控制种群密度使其接近E*.因为过度拥挤或过度稀疏都不利于种群的生存和繁殖,所以适度合理的种群密度才是使人们从中获得最大经济收益的重要因素.此外,通过对种群密度进行人为控制也能够实现种群可持续发展的目标.