与群作用于集合的等价类计数有关的组合恒等式

唐善刚

(西华师范大学数学与信息学院，四川 南充 637009)

组合恒等式是组合数学研究领域的一个热点问题[1-2]，它在概率论、统计学、数论、密码学以及数学的其它领域也有着广泛的应用，研究新的组合恒等式在数学理论与应用层面都是一项有意义的工作。现有文献对组合恒等式的研究已得到很多重要的成果，如文献[3-6]得到了若干与格路计数有关的组合恒等式，文献[7]应用复变函数、组合与图论方法论研究的是与nn-1有关的组合恒等式的新证法及其应用，文献[8]得到若干与正整数的有序分拆有关的组合恒等式，文献[9]应用母函数的组合分析技巧得到一些新的组合恒等式，文献[10-11]研究的是与Vandermonde恒等式有关的一些新的组合恒等式。本文应用有别于文献[3-11]的Burnside-Polya计数法[1]、容斥原理[12-17]等组合分析方法与置换的轮换分解[18]的群论方法的巧妙结合，得到与恒等群、循环群和二面体群作用于一类映射集的等价类的计数有关的组合恒等式，这些组合恒等式较之于文献[3-11]的结果是完全不同的类型、且是新颖的，也丰富、拓宽了组合恒等式的研究范围、方法与结果，并对发现新的组合恒等式也有一定的应用价值。

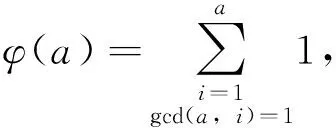
(1)

(2)

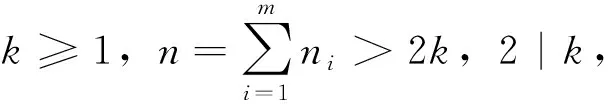
(3)

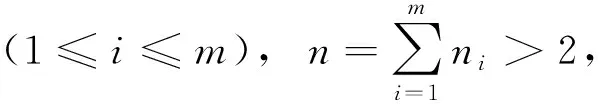
(4)

我们将给出式(1)～(4)的一种统一的组合证明，为此，需要用到下面的一些预备知识。

1 预备知识

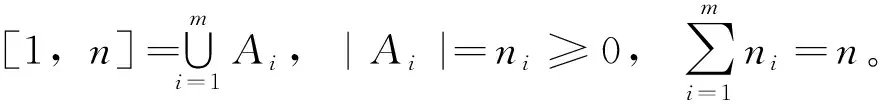
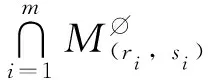
定义1对任意u∈Z，定义[1,2k]上的置换θu为：

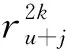
定义2对任意u∈Z，定义[1,2k]上的置换ηu为：

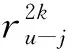
引理1令G0={θ0}，G1={θu|u∈Z}，G2={θu|u∈Z}∪{ηu|u∈Z}，则G0是恒等群、G1是2k阶循环群、G2是4k阶非循环群(一般称其为二面体群)。

定义3定义Gv×M→M的映射gv为：

gv:Gv×M→M(σ,f)→f′，

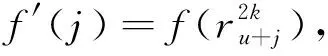
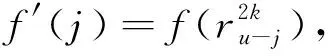
容易证明gv(v=0,1,2)满足“群在集合上的作用”的公理化定义[18]，即有下面的引理2。

引理2gv是群Gv在M上的作用，这里v=0,1,2。

定义4设λ,μ∈M，定义λ与μ之间的二元关系Rgv为：存在σ∈Gv，使得λ=gv((σ,μ))，一般将λ=gv((σ,μ))记之为λRgvμ，这里v=0,1,2。

根据等价关系的公理化定义[18]，有下面的引理3。

引理3Rgv是M上的元素之间的等价关系，这里v=0,1,2。

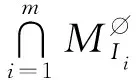
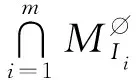
定义5设λ∈M，根据引理3，称{μ∈M|μRgvλ}是群Gv作用于M的等价类(或称轨道)。

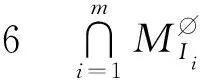
引理7[14-15]对于非负整数d,s,t，且s≤t，令

则有

其中约定：

有了上述准备工作，我们发现组合恒等式(1)～(4)可由如下的组合计数问题来得到。

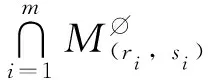
2 定理的证明

下面给出定理1～定理4的一种统一的组合证明，需指出的是，以下证明过程中涉及到的所有符号、记法及其数学含义与第1节中交代的是完全一致的，如无必要，无需另作说明。

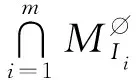
(5)

其中v=0,1,2。

根据文献[14]的推论1中的容斥原理，即得

(6)

其中v=0,1,2。

下面给出求Qv(t1,,tm)的计算公式的具体方法(v=0,1,2)。

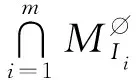
(7)

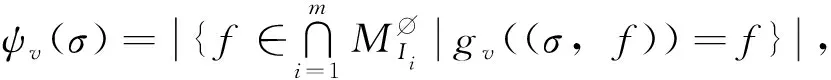
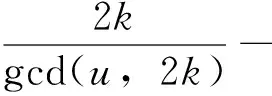
(8)

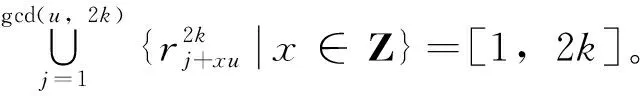
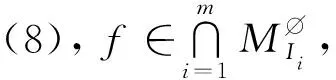
(i) 对任意u∈Z，不妨设gcd(u,2k)=d，则有

情形2当σ=ηu，u∈Z。由置换的轮换分解[18]，不妨设ηu的两两不相交的轮换分解为：

(9)

(ii) 对任意u∈Z，且u为奇数时，则有

(iii) 对任意u∈Z，且2|u，k为奇数或4|u，2|k时，则有ψ2(ηu)=0

(iv) 对任意u∈Z，且2|u，2|k，4不整除u时，则有

将上述ψ1(θu)与ψ2(ηu)的计算公式代入式(7)，即得

(10)

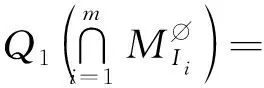
(11)

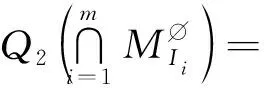
(12)

其中k≡1(mod 2)。

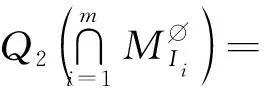
(13)

其中k≡0(mod 2)。

注意到，对任意的非负整数ti≤ni(1≤i≤m)，有如下的式(14)。

(14)

其中Ii⊆Ai且|Ii|=ti(1≤i≤m)，v=0,1,2。

于是，将式(10)～(13)分别代入式(14)，即得Qv(t1,,tm)的如下的计算公式(v=0,1,2)。

(15)

(16)

(17)

其中k≡1(mod 2)。

(18)

其中k≡0(mod 2)。

最后将式(15)～(18)代入式(6)，即得

(19)

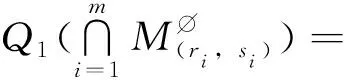
(20)

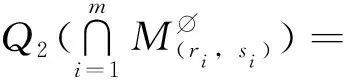
(21)

其中k≡1(mod 2)。

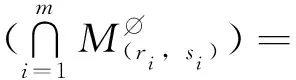
(22)

其中k≡0(mod 2)。

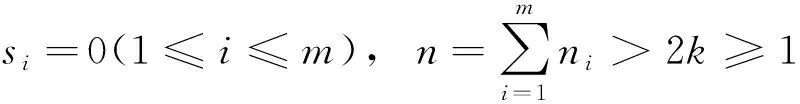
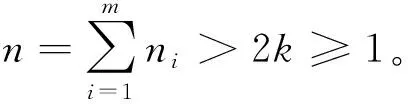
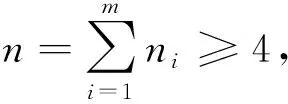
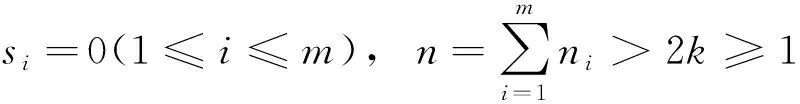
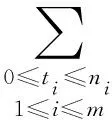
(23)

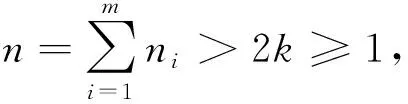
(24)

将式(24)代入式(23)，即得

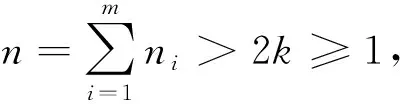
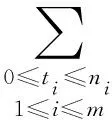
(25)

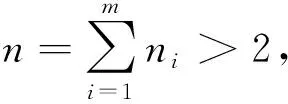
(26)

将式(26)代入式(25)，即得

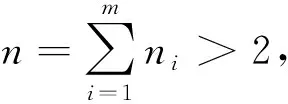
至此，定理1～定理4得以证毕。