Bloch型空间上加权微分复合算子的一些特征

侯晓阳，秦 春

(1．温州商学院基础部，浙江温州 325035；2．温州大学数理与电子信息工程学院，浙江温州 325035)

设D为复平面ℂ上的单位圆盘，H（D）表示D上的所有解析函数全体，φ为D上非常值的解析自映射．对任意的α＞0，定义

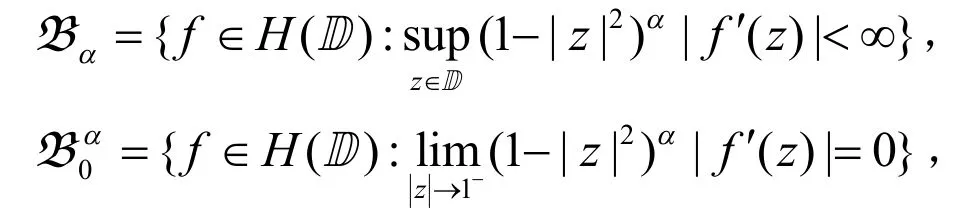
分别称为Bloch 型空间和小Bloch 型空间．易知它们在范数下为Banach 空间．

设D=D1为微分算子，即D1f=f′，Dnf=f(n)，特别地，D0f=f．对任意u∈H(D)，定义加权微分复合算子

若n=0，则就是加权复合算子uCφ:uCφf(z)=u(z)f(φ(z))，如果再有u(z) ≡ 1，则为复合算子Cφ．

文[2-3]研究了Bloch空间和小Bloch空间相关的复合算子Cφ的有界性和紧性问题，关于Bloch空间上的加权复合算子uCφ可见文[4-5]及其相应的参考文献．Li 等在文[6]中研究了不同Bloch型空间之间的微分复合算子DCφ，文献[7]研究了单位圆盘上从BMOA 空间到Bloch 型空间的加权微分复合算子的有界性和紧性，该结果的推广可见文[8-9]．Stević 在文[10]中研究了Bloch型空间Bα上指标α与微分复合算子DCφ的有界性和紧性的关系，本文推广了该文的几个结论．更多关于不同空间上加权微分复合算子的有关结论可见[11-13]及其参考文献．

1 主要结果

文[8-9]从解析自映射φ和解析函数u之间的关系讨论加权微分复合算子在Bloch型空间Bα和小Bloch 型空间上的有界性和紧性问题，得到如下结论．

定理1[8]设0＜α，β＜∞，n∈ℕ+，u∈H(D)，φ为D上非常值的解析自映射，则

i）:Bα→Bβ是有界算子的充分必要条件是：

ii）:Bα→Bβ是紧算子的充分必要条件是:Bα→Bβ有界，且

定理2[9]令0＜α，β＜∞，n∈ℕ+，φ为D上非常值的解析自映射，则是紧算子的充分必要条件是：

本文从指标α,β的角度继续讨论加权微分复合算子在Bloch型空间和小Bloch型空间上的有界性和紧性问题，结合上述两结论，得到：

定理3 令0＜α，β＜∞，u∈H∞(D)，n∈ℕ+，φ为D上非常值的解析自映射，则有：

i）若β≥α+n，则:Bα→Bβ是有界算子；

ii）若β＞α+n，则:Bα→Bβ是紧算子；

iii）若β＞α+n，则是紧算子．

定理4 令0＜α＜∞，0＜β＜1，n∈ℕ+，u∈H(D)，φ为D上非常值的解析自映射，且则下面三条等价：

i）:Bα→Bβ是有界算子；

ii）:Bα→Bβ是紧算子；

iii）u∈Bβ，

本文出现的字母C表示与变量z,w无关的常数，为方便起见，不同情况下可表示不同的常数．

2 定理3的证明

在证明之前，先给出如下引理（文[14]引理2.2）．

引理1 设α＞1，β＞1，u,φ∈H(D)，且如果则

于是由引理1 可知：

由Schwarz-pick 不等式及（7）式，可得：

由（8）式和（9）式及定理1 i）可知结论成立．

ii）因为β＞α+n，则存在ε＞0，使得β≥α+n+ε，从而

胰腺原发性平滑肌瘤多为实性肿块，镜下见大小一致的梭形细胞呈纵横交错的束状排列，细胞无或少量有核分裂象，多无出血、坏死。免疫组化示SMA和Vimentin阳性[1]。CT表现为胰腺内稍低密度影，边界较清，动脉期呈轻度不均匀强化，以边缘强化为主，门静脉期及延迟期显著均匀强化，强化程度与正常胰腺组织相仿或高于正常胰腺组织。张涛和李绍东[3]报道胰腺原发性平滑肌瘤MRI表现为胰腺结节性病灶，边界清晰，呈稍长T1、长T2信号影，信号不均，增强后不均匀强化，DWI示病灶扩散明显受限，呈高信号。

则由引理1 可知：

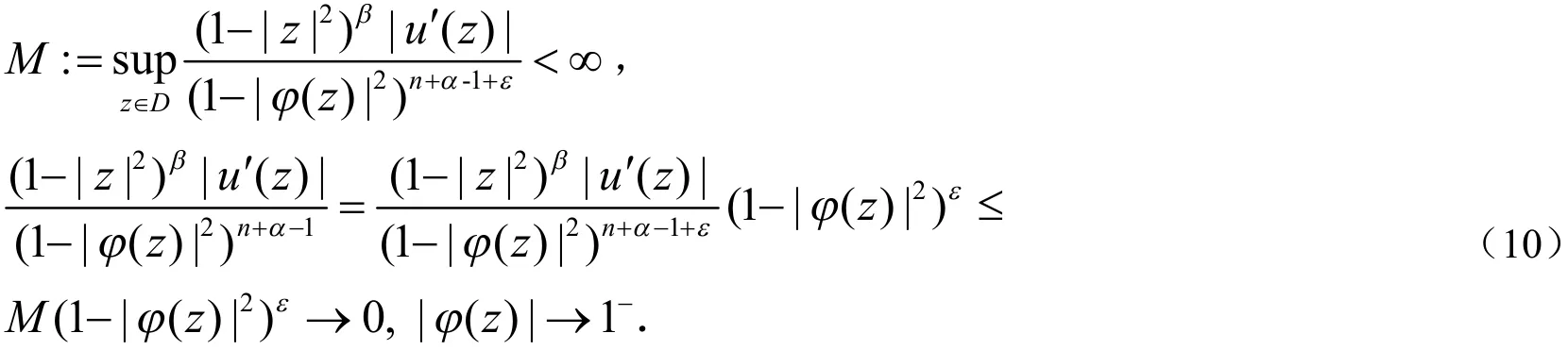
应用Schwarz-pick 不等式及条件u∈H∞(D)可得：

由（10）式和（11）式以及定理1 ii）可知结论成立．

iii）结合定理2 类似ii）可证．

3 定理4的证明

下面的引理是紧性判断的常见工具，类似文[15]命题3.11 可证．

引理2 令u∈H(D)，φ为D上非常值的解析自映射，则算子:Bα→Bβ是紧算子，当且仅当对任意紧子集上一致收敛于0的有界序列{fm}∈Bα，有

定理4 的证明：ii）⇒i），显然成立．

i）⇒iii）．因为:Bα→Bβ有界，则由定理1 i）可知：

于是有：

从而，u∈Bβ，

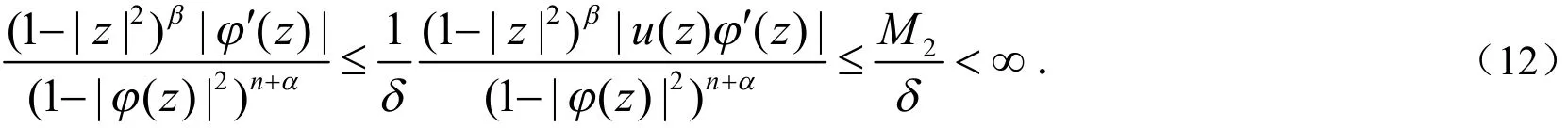
当0＜β＜1＜n+α时，结合（12）式可得：

由（13）式及文献[4]中推论2.4（或在定理1 i）中令n=0，u=1）可知，Cφ:Bβ→Bβ有界，且由（13）式易知:

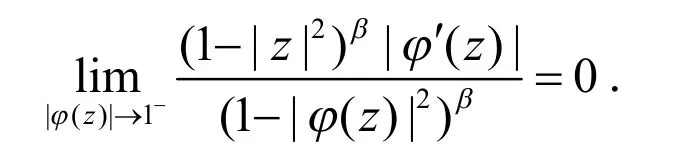
结合文献[4]中推论3.2（或在定理1 ii）中令n=0，u=1）可推得：Cφ:Bβ→Bβ是紧算子．根据文献[15]定理4.5 可得||φ||∞＜1．

iii）⇒ii）．假设{fm}m∈N为Bα中的有界序列，且在D的紧子集中一致收敛到0，由引理2，只需证明

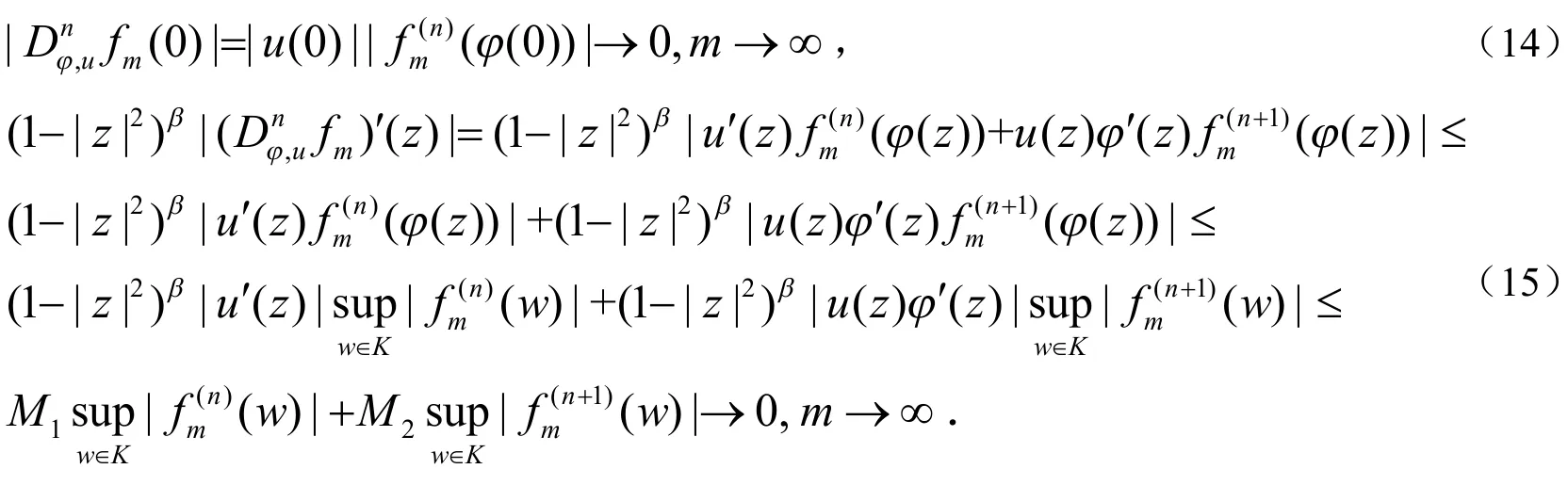
由式（14）式和（15）式结合引理2 即得:Bα→Bβ为紧算子．