基于BP神经网络的排队时间预测算法研究

潘樱丹，钱佳丽，何妍蕾，唐震洲

(温州大学数理与电子信息工程学院，浙江温州 325035)

随着现代生活节奏的加快，如何更高效地利用时间已然成为生活的重要需求．然而笔者观察到，现有的许多排队机制都在无形中浪费人们的时间，例如银行取号排队，人们常因为担心过号而在大厅等候，虽然存在着一些能够显示预计排队时间的APP，但其预测的排队时间往往来自于大数据的平均值，一般和当天的实际情况不相符．因此研究排队时间预测算法及其应用极具现实意义，将理论上的预测算法带入现实生活，使人们避免为排队浪费时间，从而获得更高效便捷的生活方式．

在排队时间预测领域的现有研究中，一般采用排队论和传感技术的结合，例如在机场利用WIFI 进行室内定位得到排队区域的客流量，然后再根据排队论模型预测排队时间[1]．但是排队论在等待时间的计算上不够动态，且传感技术的部署成本较大，不能广泛使用．因此需要更动态、成本更低的算法，比如决策树算法，核心思想是选取具有最高信息增益的属性，常用于预测数据的类别[2]；支持向量机，一种基于结构风险最小化原则的机器学习方法，适用于小样本[3]．在多种预测算法中，BP 算法具有自学习、自组织、高容错性的特点，预测较为精确，且在国内外应用广泛．例如，模糊优选神经网络模型可以用来预测泥石流的平均流速，该模型在对云南蒋家沟黏性泥石流平均流速的预测中取得了很大成果[4]；BP 算法在股票预测中也有所应用，BP 神经网络的权值初始化在进行改进之后能够较为准确的预测股价[5]；此外，BP 算法也应用于公交车到站时间的预测，通过公交车到站的历史数据和实时数据对BP 算法的训练，能够得到相当准确的公交车到站预测时间[6]．因此，本文选择了BP 算法来预测排队等待时间．经过实地考察测试以及误差分析，结果表明，利用历史排队时间对BP 算法进行训练能够较为准确地预测当前用户的排队等待时间．

1 系统模型

本文采用的预测算法模型基于传统BP 算法同时有所修改，具体模型如图1．

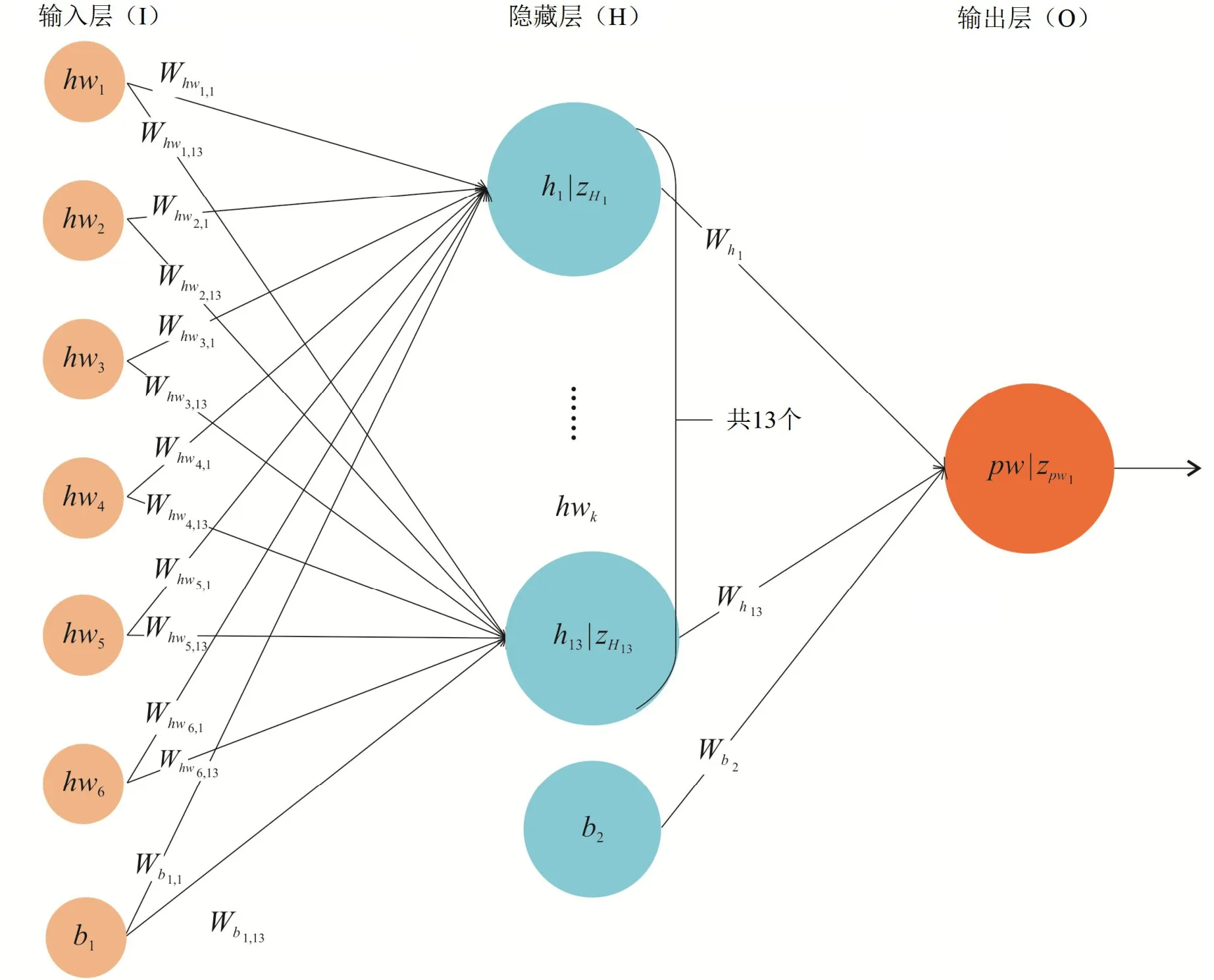
图1 BP 神经网络结构图Fig 1 The Structure Chart for BP Neural Network

1.1 BP时间预测算法的正向传输

以当前用户的前6 名的真实排队时间或预测等待时间作为输入层，如果此6 名用户已结束排队则具有实际等待时间，否则只有算法给予的预测等待时间．以6 名用户的预测等待时间作为输入层容易增大误差，解决方式详见后文．隐藏层有13 个单元（1.3.2 小节会详细阐述如何确定隐藏层单元个数），输出层为当前用户的预测等待时间pw，以分钟为单位．基础算法如图1 所示．

隐藏层单元hj的输入加权和：

式（1）中，hwk，k=1,2,3,4,5,6，为输入层单元，以分钟为单位，另有阈值b1=1；Whwi,j，i=1,2,3,4,5,6，j=1,2,3,…,13，为输入层到隐藏层权重，b1的权重为Wb1,j，j=1,2,3,…,13．

隐藏层单元hj的输出Zhj：

式（2）中，Zhj，j=1,2,3,…,13，是隐藏层激活后的输出，在隐藏层和输出层，均采用sigmoid函数作为激活函数[7]．

输出层单元pw的输入加权和输出为：

式（3）中，hk，k=1,2,3,…,13，是13 个隐藏层单元，另有阈值b2=1；隐藏层到输出层权重为Whk，k=1,2,3,…,13，b2的权重为Wb2，权重矩阵的初始值皆随机产生．

式（4）中，Zpw为输出层激活后的输出，也是算法最终输出的预测结果，同时显示给用户．

1.2 BP神经算法的反馈机制

由于BP 神经网络最初的权重为随机产生，如果不根据实际值和预测值的误差调整权重，BP神经网络将无法准确地适应具体情景．因此，必须使用历史数据对BP 算法加以训练[8]．本文的预测算法模型的反馈机制分为两部分：①输入层--＞隐藏层、隐藏层--＞输出层的权重更新；②某用户结束等待后，其后用户的输入层更新．

1.2.1 层与层之间的权重更新

首先，根据用户的实际等待时间和预测等待时间得到总体误差；其次，对输入层--＞隐藏层、隐藏层--＞输出层的权重进行一一更新．下面以隐藏层--＞输出层的权重更新为例进行阐述，如图2所示．

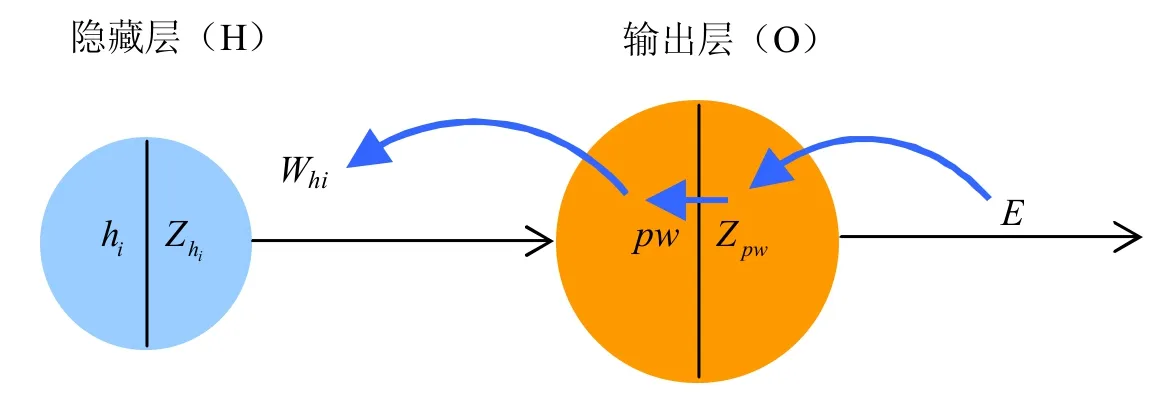
图2 BP 神经网络的反馈机制（隐藏层--＞输出层的权重更新）Fig 2 The Feedback Mechanism for BP Neural Network(hidden layer --＞output layer weight updating)

总误差的计算：

式中，target 为用户的实际等待时间，output 为预测等待时间．

根据梯度下降法，隐藏层到输出层的权重更新为：

隐藏层的阈值权重更新：

（8）式中，η为学习率，本文取0.3．下文会讲到如何确定学习率．

输入层--＞隐藏层的权重更新与隐藏层--＞输出层同理，只是计算对象变化．

1.2.2 用户的输入层更新

该机制的主要目的是解决预测等待时间作为输入层带来的误差问题．在一个用户结束等待时将产生实际等待时间，算法利用其实际等待时间与预测等待时间的误差进行权重更新，更新完毕后迭代更新其后所有用户的输入层和预测等待时间，具体过程可见图3．

1.3 BP时间预测算法的关键参数处理与确定

1.3.1 学习率的确定

学习率是权重更新算法的重要参数，在BP 算法中学习率的确定很重要．因为BP 算法学习率一经确定就不再改变，并且决定后期权重更新的收敛速度[9]．本文通过多次数据测试确定如下学习率：

在选定0.2 的学习率时：MSE=70.0；

在选定0.3 的学习率时：MSE=60.2；

在选定0.4 的学习率时：MSE=63.5；

在选定0.5 的学习率时：MSE=68.6；

在选定0.6 的学习率时：MSE=71.3．

通过多次比较均方差，确定0.3 为最适合本模型的学习率．

1.3.2 隐藏层节点数的确定

根据Komogorov 定律，一个具有m个输入层节点、2m+1个隐藏层节点、n个输出层节点的三层网络，可以精确实现任意连续函数[10]．在本文的BP 算法模型中，以当前用户的前6 名用户的等待时间作为输入层节点，因此选择隐藏层节点数为13 个．

1.3.3 输入层输出层的数据处理

在数据处理方面，由于输入层和输出层的实际值单位为分钟数值过大而权重过小，会导致权重无法影响数据变化和权重无法进行更新而预测失败，因此在产生输入层和输出层实际值时先进行归一化处理．我们采用的归一化处理方式为最大值归一化[11]：在输入的所有历史数据中选出最大的等待时间，输入层即为实际等待时间/最大等待时间．输入层归一化处理的公式为：

其中，hwmax为所有输入层历史数据中的最大等待时间．而输出层归一化处理的公式为：

其中，pwmax为所有输出层历史数据中的最大等待时间．

1.4 BP时间预测算法模型的具体流程

该算法对排队等待时间预测的具体实施流程如图3 所示：

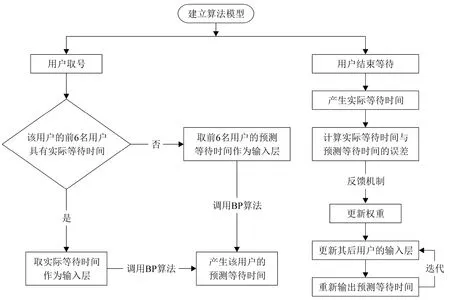
图3 BP 时间预测算法的具体流程Fig 3 The Detailed Flow for BP Time Prediction Algorithm

1）建立一个输入层为6、隐藏层为13、输出层为1、学习率为0.3 的BP 算法模型；

2）使用来自合作商家的历史数据对权重随机的BP 算法进行训练，以适应当前的情形；

3）用户进行取号操作，调用历史数据库查看其前6 个用户是否有实际等待时间，如果有则采用，否则使用预测等待时间作为该用户的输入层．调用BP 算法，显示预测结果；

4）当一个用户结束等待时，将其实际等待时间和预测等待时间置入算法中进行权重更新，更新完毕的权重和该用户的实际等待时间立刻用于其后用户的等待时间预测．

BP 时间预测算法伪代码如下．

输入：前6 名用户的排队时间

输出：预测排队时间

2 预测结果分析

将上文所述模型应用于实际排队时间预测．在某餐厅，晚餐时间段（16: 00- 20: 00）实地考察了67 组数据，预测误差基本在8 分钟以内，其中60组数据的实际值和预测值的对比图如图4所示：

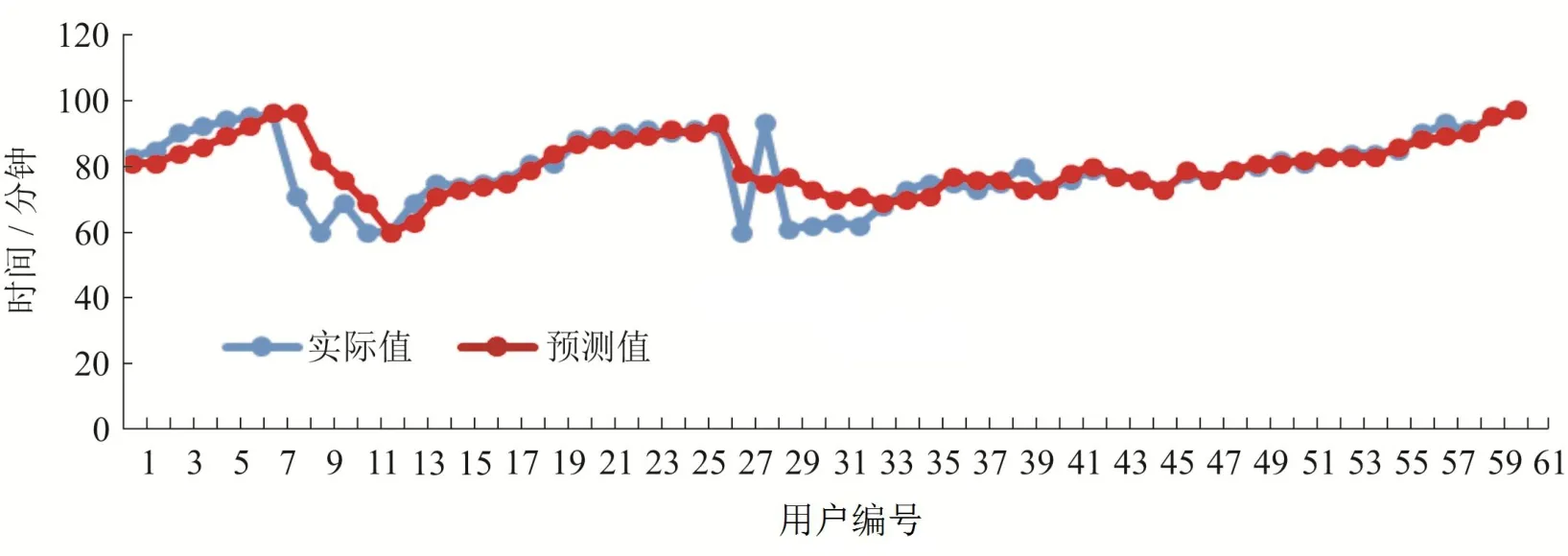
图4 60组数据的实际值和预测值的对比图Fig 4 The Area Chart for Actual Value and Predicted Value from 60Sets of Data

60组数据的分析结果：MSE=60.2；RMSE=7.75．在图4 中可以观察到几组等待时间异常的数据，例如某组数据的等待时间近100分钟，但其后几组数据的等待时间骤降至70分钟左右，这几组异常数据是由人们行为的不稳定性导致的．当天用餐的时间、天气、心情都可能影响用餐人的用餐速度，进而影响预测结果的准确性．在剔除这几组数据的影响后，可以明显发现均方差的降低．剔除几组异常数据后的均方差为：MSE=5.31．从均方差的大幅度降低可以见得，在大部分时候，算法预测的准确率是比较高的，在偶然的不稳定因素出现时，算法才出现局部的偏差．但我们不能因此而忽略了这种不稳定因素的存在，因此我们后续的研究方向是，在考虑前6人的等待时间外，把当天的其它因素也转化成算法的一个特征值以减少这些特殊行为带来的误差，提高算法的容错能力．

3 结 语

日常生活中经常会出现长时间的排队等待现象，为了减少枯燥的等待行为和避免过号现象，本文提出了一种基于BP 算法的排队时间预测算法．经过实地考察、数据测试分析，证明该BP算法模型可以较好地为人们预测较为准确的排队时间．后续研究中我们会继续深入，希望能够进一步减少误差，为人们提供更高精度的预测．